火星次表层探测雷达信号分析与处理∗

(中国电子科技集团公司第三十八研究所,安徽合肥230088)

0 引言

基于火星的特殊位置以及特殊环境,从20世纪60年代人类就开始对其探索。从1960年10月10日前苏联发射人类首颗火星探测器(Mars)开始,人类揭开了火星探测的序幕[1]。进入21世纪,火星探测成为深空探测的研究热点,美国、欧空局、俄罗斯、日本等大国或机构竞相提出火星探测计划,最为典型的火星环绕器次表层探测任务包括欧空局“火星快车”上搭载的火星次表层电离层先进探测雷达(Mars Advanced Radar for Subsurface and Ionosphere Sounding Radar,MARSIS)、美国“火星勘测轨道器”上搭载的浅表层探测雷达(Shallow Subsurface Sounding Radar,SHARAD)[2],其探测科学任务除了火星表面的物质构造、地质分布等,还承担着对火星电磁场和电离层的特性研究任务。相对而言,MARSIS因其信号带宽(1 MHz)比较窄,对冰层的厚度分辨率较弱;SHARAD不仅在分辨率上加以提高(带宽达到10 MHz),且以很简化的设计提供突出的探测性能,Chirp信号载波直接合成与接收机射频直接采样降低了系统复杂度、重量、功率,提高了可靠性,系统搭载于火星轨道探测器。连续3年的在轨测量结果表明设计目标完全满足,为火星探测提供了高质量的科学数据。但是,它们基本上是把原始数据传回到地球,然后线下进行数据处理。对于火星探测任务,因为距离太远,大量的数据传输一直是科学家较为头疼的问题。而本文就是通过对火星次表层探测雷达回波进行仿真模拟,对回波信号进行星上实时处理,得到聚焦以后的数据,直接传回地球,虽然存在一定的风险,但是显然能够大大降低数据量,这对于了解火星、走进火星,降低探测任务风险提供了更加有力的保证[3]。

1 探测原理分析

图1为雷达探测火星次表层结构示意图。假设火星次表层为两层的分层模型,其中上层介质的介电常数为ε1,损耗角正切为tanδ1,下层介质的介电常数为ε2,损耗角正切为tanδ2,定义上层介质与空间的交界面为火星表面,上层介质与下层介质交界面为次表层[4]。

图1 雷达次表层探测视图

雷达平台高度为H,以θ的波束角向火星表面发射电磁波,上层介质的厚度为D。A为星下点,电磁波到达表面,反射的电磁波直接被雷达接收机接收,定义为A点的回波,其时间延迟为2H/c,c为真空中的光速。投射电磁波传输到次表层星下点B点,被下层介质反射,再经过上层介质的折射返回到雷达接收机,定义为次表层星下点B点的回波,其时间延迟为由于火星表面地形的起伏,使得雷达也会接收到火星表面C点的回波,如果其时间延迟与次表层星下点回波相同,那么很可能会淹没次表层星下点回波,因此表面非星下点回波和次表层星下点回波的区分能力是雷达探测任务以及火星设计应该考虑的重要因素。

根据电磁波传播原理,显然次表层的单元回波会被表层同距离单元的回波淹没,在回波时域上很难区分开来。然而,星下点的次表层单元的回波多普勒和表层同距离门单元回波的多普勒不在同一个多普勒环,利用这一点,可以对实际回波进行距离方位聚焦处理,从而在频域上得到地质分层信息。

2 雷达回波分析

2.1 雷达探测回波模拟流程

火星次表层探测雷达回波模拟的流程包括:通过真实DEM或者数值模拟方法获取表面地形,计算火星表面和次表面散射,根据发射脉冲的波形时域卷积得到回波波形,流程如图2所示。

图2 回波模拟流程示意图

其中,表面和次表面散射的计算包括:KA近似计算表面反射,由射线追踪法、几何光学和KA近似计算次表面的散射。电磁波在火星表面和次表层的散射、投射和衰减等,对于提取次表面星下点回波、确定火星次表层结构和反演火星次表层参数等具有重要的意义。

2.2 雷达探测回波计算原理

Kirchhoff近似,又称为切平面近似,粗糙面任意一点处的表面场用该点的切面场来近似。次表层雷达探测电磁波反射的计算如图3所示,雷达位于点P0(x,y,z),入射场于P1处发生反射和投射,反射场产生感应电流形成了火星表面回波。P1处的投射场在上层内向下传播至次表层P2(x,y,z)处发生反射,反射场在层1内向上传播,到P3(x,y,z)点处产生透射,该透射场在P3处产生感应电流,形成了次表面回波[5]。

图3 雷达探测电磁波反射示意图

在图3中,假设点P1处的入射场为

由Kirchhoff近似,P1处的反射场可以表示为

由Stratton-Chu积分方程,P1所在面元1在雷达所在位置点P0处辐射的电场为

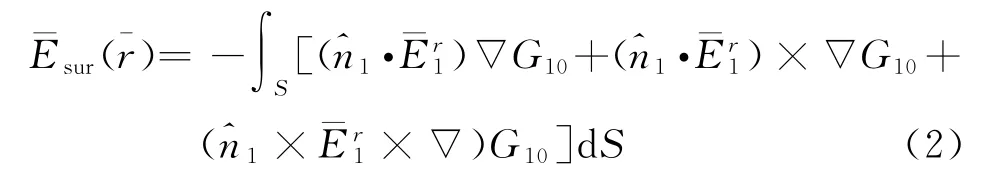
式中,Green函数G10为

同理,可得次表层散射场为

式中,Green函数G30为

实际计算时,火星表面和次表面被划分为大量离散的小单元,将距观测点P0射程距离为r n(第n个距离单元)的所有面元产生的散射场相加,得到雷达接收到的表面和次表面散射场分别为

雷达总回波场为

然后对其进行线性调频信号调制得到雷达回波信号。

2.3 仿真试验分析

为了方便仿真,假设环绕器轨道为圆形轨道,火星位于轨道中心位置,环绕器在特定的短时间内认为是切于火星球面匀速飞行。

输入仿真参数如表1所示。

表1 仿真参数设置

通过上述数据仿真处理,然后对关注的5 km范围进行截取,其时域三维回波如图4所示。

图4中,图4(a)为时域回波,图4(b)为脉压后的回波。从图中可以观察到,从时域回波很难看出分层现象,正如前面分析的一样,次表层回波被表层回波淹没。这里便于验证,对其进行多普勒分析,从频域加以观察。

图5为回波的频谱分析图,其中图5(b)为图5(a)频谱的零频谱线,从零频谱线图可以明显看到,在第50和100个距离单元处有明显的尖峰,分别比表层回波低了10.54 dB和27.51 dB,这正是验证了仿真设置的分层参数,同时也验证了算法的有效性。

图4 模拟的时域回波

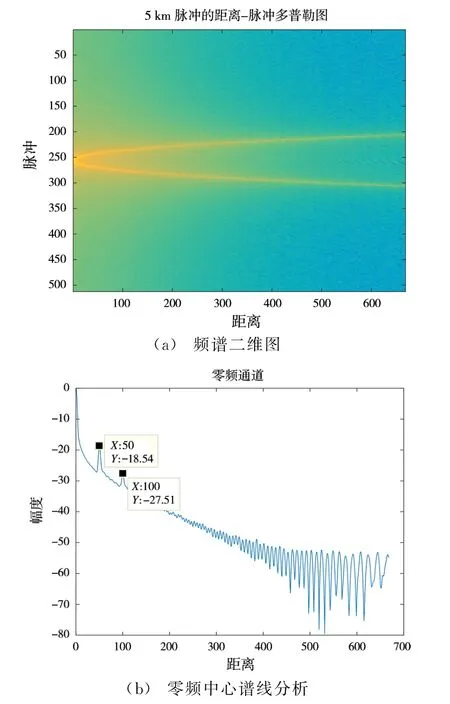
图5 回波频谱分析图

3 星上实时处理分析

如果采用星上实时处理,其可靠性一定要保证,这对于算法的选择尤为重要。SAR实时成像处理可以在平台运动的同时实时获得SAR图像,对于实时监测和战场侦察具有重要意义。目前常用的成像算法有改进RD,CS,Ω-k,BP等。对于实时处理而言,必须在满足雷达分辨率、测绘带等指标的情况下,尽可能地降低运算时间,因此需要考虑不同算法的成像性能及处理流程。考虑到硬件资源、实时性、方位聚焦能力等多方面因素,本文采用BP算法来实现聚焦处理[6]。

3.1 BP算法聚焦处理仿真

BP算法起源于计算机断层扫描技术,是一种精确的时域成像方法。该方法假设发射波是冲激球面波,通过回波在时域的相干叠加来实现高分辨率成像。对于线性调频体制的雷达,首先在距离向上利用匹配滤波进行脉冲压缩处理,通过回波曲线在时域上的相干累加来实现,适用于任意的孔径,相应的距离徙动也得到了校正。

其具体实现过程如下:对于t a时刻发射的线性调频脉冲,首先进行距离压缩,然后依据所求网格点与传感器位置之间的距离R寻找该点在距离压缩后的信号中的位置,将此位置处的散射系数填入到相应的网格中去,从而实现后向投影的过程。

对于该脉冲,用这种方法求出场景中所有网格点上的值,然后再对下一时刻的脉冲重复同样的步骤,并将场景中相应位置处的散射系数进行累加。由于斜距R并不一定位于距离向信号的整数采样点上,因此要获得距离R处精确的散射系数还需要进行插值。BP算法的流程如图6所示[7]。

图6 BP算法流程图

对2.3节的时域回波数据通过上述BP算法聚焦处理,得到如图7所示结果。

从聚焦结果,可以非常明显地看到三层地形,根据仿真设置,显然依次为表层、次表层、第三次分层情况。

图7 BP算法聚焦结果

3.2 聚焦算法对平台运动误差的敏感分析

为了分析算法对平台运动误差的敏感度加以分析,考虑到面回波无法体现单独目标回波特性,在仿真中,只对一个杂波单元加以分析,对星下的一点采用BP算法进行聚焦处理,方位加权50 d B。试验分别对不加随机误差、方位向加随机误差、俯仰向加随机误差加以仿真,而且对随机误差从无到有、从大到小逐步仿真,得到如图8～图11、表2～表3所示结果。

从上述仿真结果可以看到,水平误差和垂直误差的影响不同,且影响程度不同。在不断加大水平误差时,其主瓣会不断展宽,这会直接影响方位分辨率的大小。主副积分比和主副比逐渐减小,在水平误差加到150 m的情况下,无法满足成像要求的主副比30 dB,且主瓣展宽严重;当不断加大垂直误差时,可以看到其不会影响主瓣宽度,但是主副积分比和主副比剧烈减小,直接影响聚焦效果。在保证主副比一定的情况下,其垂直误差容限很小,在±0.5 m左右。

图8 没有加入随机误差的方位向聚焦效果

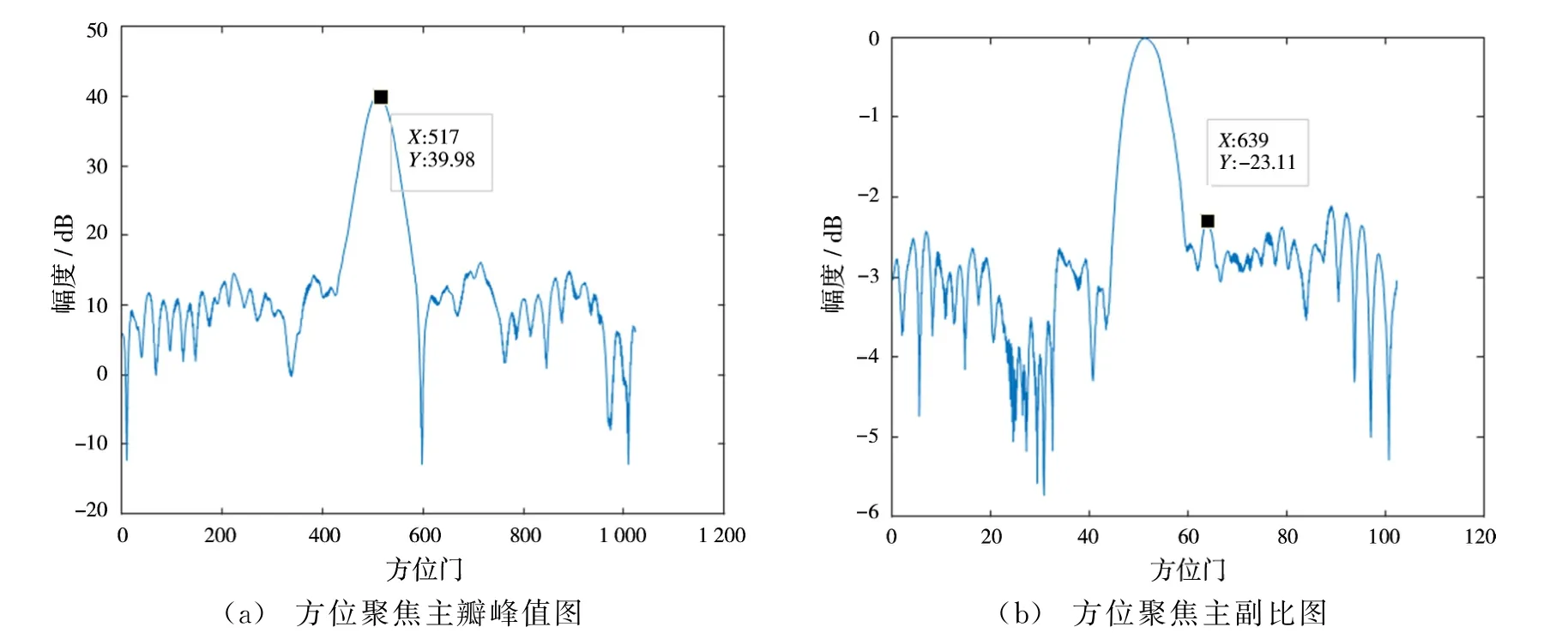
图9 加入水平位置随机误差200 m的方位向聚焦效果

图10 加入垂直位置随机误差0.1 m的方位向聚焦效果

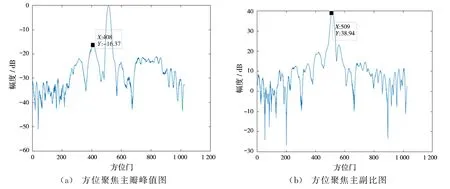
图11 加入垂直位置随机误差0.8 m的方位向聚焦效果

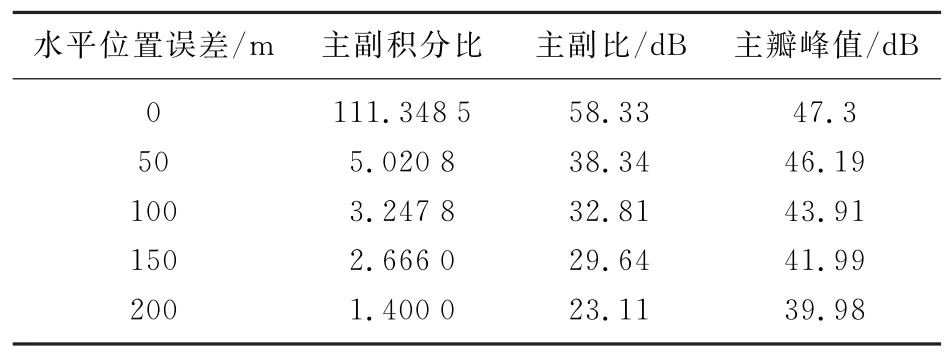
表2 水平位置误差所形成的影响

表3 垂直位置误差所形成的影响

4 结束语

通过对火星次表层探测雷达的任务进行深入分析,从火星环绕器次表层探测的原理出发,基于项目工程实际,对次表层雷达的探测任务回波加以仿真分析,并进一步对星上实时处理算法的选取原则作了简要说明,分析了BP算法的成像原理,最后通过分析平台水平和垂直向的误差对成像结果的主副瓣积分比、主副瓣比、主瓣峰值水平的影响,对星上实时处理流程以及算法容许的平台误差进行了计算机仿真。但是,目标的仿真模型还不够完备,具体工程实施中,轨道不是圆形而是椭圆,这样聚焦过程就会存在严重的距离走动现象,同时,火星表面复杂度还难以预测,这是后续需要努力的方向。

[1]欧阳自远,肖福根.火星探测的主要科学问题[J].航天器环境工程,2011,28(3):205-217.

[2]曹志国,常文革,李召阳,等.星球次表层探测中地杂波抑制技术研究[J].雷达科学与技术,2013,12(6):650-651.

[3]IORIO M,MECOZZI R,SEU R,et al.GPR Missions on Mars[C]∥IEEE International Geoscience and Remote Sensing Symposium,Barcelona,Spain:IEEE,2007:4095-4100.

[4]KUREKIN A,RADFORD D,LEVER K,et al.New Method for Generating Site-Specific Clutter Map for Land-Based Radar by Using Multimodal Remote-Sensing Images and Digital Terrain Data[J].IET Radar,Sonar and Navigation,2011,5(3):374-388.

[5]CROCI R,SEU R,FLAMINI E,et al.The SHAllow RADar(SHARAD)Onboard the NASA MRO Mission[J].Proceedings of the IEEE,2011,99(5):794-807.

[6]周琳,粟毅.基于互相关的探地雷达反向投影成像算法[J].电子与信息学报,2011,33(11):2714-2719.

[7]BIERENS L,VAN HEIJSTER R,VAN BEZOUWEN H.Data Reduction Using Real-Time On-Board Satellite SAR Processing[C]∥Fourth International Workshop on Digital Processing Techniques Applied to Space Communications,London:ESA,1994:21-30.