基于自相关函数三维熵的雷达信号分选∗
(空军预警学院,湖北武汉430019)
0 引言
随着现代雷达新体制、新技术的蓬勃发展,雷达辐射源信号的参数呈现出多变、快变的特点,雷达辐射源信号的分选技术面临着前所未有的挑战。传统分选方法的特征选取主要集中于所截获信号的常规参数。其中,利用脉冲重复间隔(PRI)进行分选的算法有很多,如序列差直方图、PRI变换以及改进的PRI变换算法[1-2]等。这些算法都是根据脉冲到达时间(TOA)的统计特性实现对脉冲的抽取,但在密集、交叠的脉冲序列中算法性能有所下降。
近年来,具有比常规参数较好稳定性的脉内特征受到广泛关注,为复杂电磁环境下的雷达信号分选提供了新的思路。目前已有很多学者将复杂度、相像系数、小波包变换等脉内特征参数运用到雷达辐射源信号的分选与识别之中,取得了一定的成效[3-5]。但这些脉内特征参数普遍存在对噪声较为敏感的问题,适用的信号调制类型也有限。针对以上问题,本文提出了一种新的分选方法。对接收到的信号首先分析其自相关函数,然后进一步提取该自相关函数的三维熵特征,即香农熵、指数熵和范数熵,以达到降维和提高分选效率的目的,最后将该三维熵特征作为雷达辐射源信号的分选参数,利用KFCM算法[6]实现分选。
1 自相关函数分析
1.1 自相关函数的定义
对接收到的信号进行脉内特征分析是指对中频波形数据进行分析,即得到该脉冲的一组离散时间序列该时间序列反映了接收信号的特点。由于信号中叠加了随机噪声,导致分析处理的时间序列是一组动态的数据,很难用一个完全确定的函数或函数组给定,但它们大都具有一定的统计规律性。为了形象地体现时间序列的内在联系,本文选用Box-Jenkins建模方法[7-8]对接收的雷达辐射源信号进行分析,其主要是依据自相关函数的统计特性,从统计的观点刻画了时间序列中的相关性。

式中,N为时间序列的长度,k为延迟数,c k为时间序列的样本协方差,其表达式为
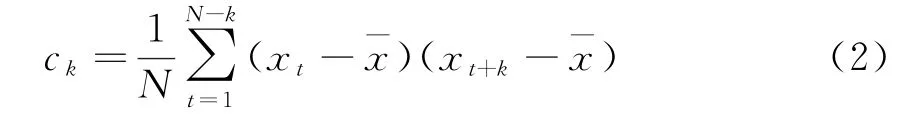
c0为时间序列的样本方差,其表达式为
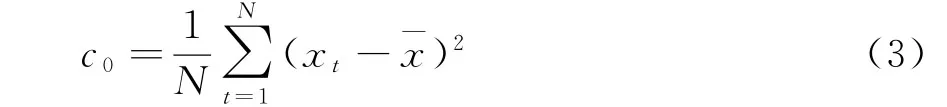
1.2 抗噪性能分析
自相关函数能够体现时间序列内部的联系和相互关系,也具有对噪声不敏感的特点,可用于有效地区别不同雷达辐射源信号。下面给出理论分析。
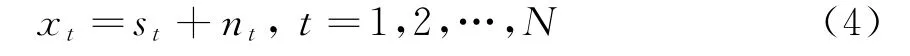
式中,s t为有用信号,n t为均值为0、方差为σ2的随机噪声,s t与n t相互独立。当N较大时,有¯x=有如下表示:
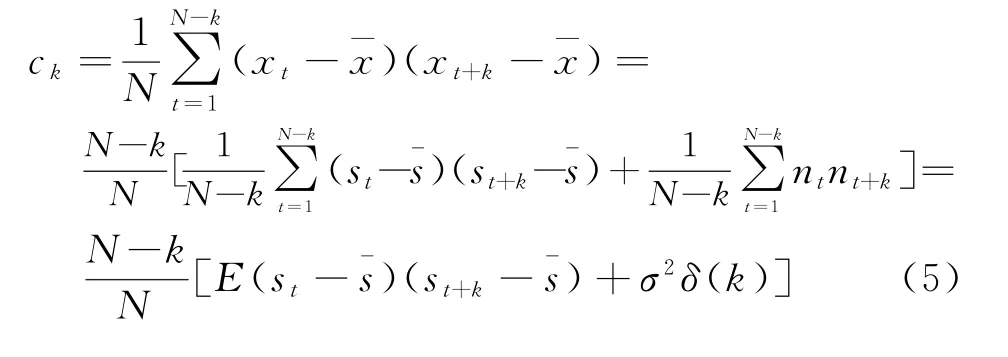
式中,E(·)为取均值,δ(·)为冲激函数。样本方差c0的表达式为
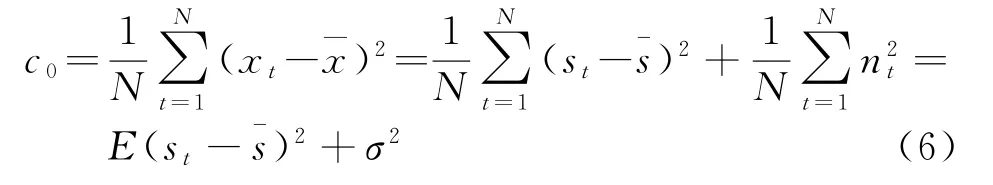
则自相关函数r k为

当无噪声时,σ2=0,则有
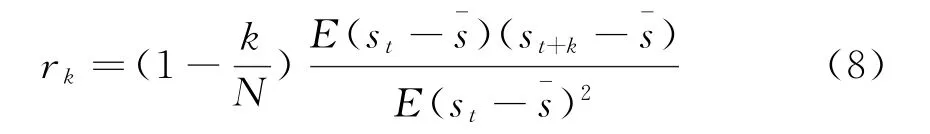
式中,根据Schwarz不等式[10](EXY)2≤EX2EY2,则可知
当有噪声时,由式(7)可知:k=0时,δ(0)=1,则有r0=1;k≥1时,δ(k)=0,则有
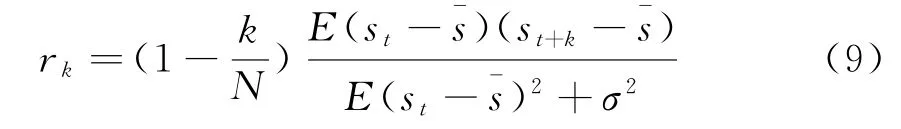
根据式(8)可以看出,当无噪声时,自相关函数值始终处于区间(-1,1];根据式(9)也可以看出,当有噪声时,σ2>0,使得在k≥1延迟数处的自相关函数值都要比无噪声时小,且噪声不影响时间序列内部的变化趋势,因此自相关函数可以在强噪声下仍旧保持信号内部的特点,即对噪声不敏感。
1.3 自相关函数仿真分析
为了形象地描述不同雷达辐射源信号的自相关特性,以信号的采样点数N=2 400、最大延迟数kmax=240为例,对单载频信号(CW)、线性调频信号(LFM)、频率编码信号(FSK)、二相编码信号(BPSK)、四相编码信号(QPSK)、线性调频-二相编码信号(LFM-BPSK)、频率编码-二相编码信号(FSK-BPSK)、非线性调频信号(NLFM)这8类信号进行分析,在无噪声情况下,给出各类信号的自相关函数,如图1所示。
由图1可知,不同调制样式信号的自相关函数存在一定的差异。为了进一步体现自相关函数对噪声不敏感的特点,以FSK-BPSK为例,给出5,10和15 dB信噪比下的自相关函数,如图2所示。
由图2可知,当信号中叠加噪声后,其自相关函数值减小,除此以外几乎无变化,且噪声越大,自相关函数值越小,这一特点从式(9)也可以看出。因此,自相关函数既保证了不同辐射源信号之间的差异性,又具有一定的抗噪性能。

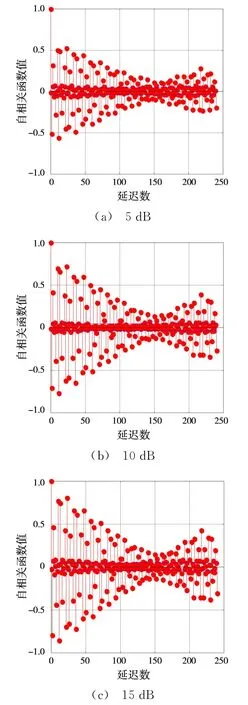
图2 不同信噪比下FSK-BPSK的自相关函数比较
2 三维熵特征的提取
从上文的分析可知,自相关函数能够较好地反映出不同雷达辐射源信号的区别,但是其维数较多,不利于直接作为特征参数进行分选,需要进行降维处理,以提高后续的分选效率。为了既能体现不同信号之间的差异,又能实现快速分选,本文选取三维熵特征进行特征参数的进一步提取。
熵是从热运动中概括出来的概念,最早由德国物理学家克劳修斯在定量描述热力学第二定律中提出,用来表征系统能量分布均匀的程度[10],也能作为对系统无序状态的衡量。从图1可知,8类信号的自相关函数体现出不同的统计规律,用熵有利于描述每类信号内部无序的状态。
2.1 三维熵特征的定义
1948年,香农(Shannon)借鉴热力学熵的概念和数理统计理论将香农熵概念引入到信息论中,以量化系统的有序化程度和信号的复杂程度。因此,本文用它来刻画调制信号内在的复杂度,信号越复杂,香农熵越大。下面给出香农熵的定义[11]:
假设一集合X={x1,x2,…,x n},则集合中各个事件发生的概率用n维概率矢量P={p1,p2,…,p n}表示,且满足两个条件由此,香农熵表达式为

香农熵在解决信号不确定性问题时有较好的效果,但也存在一定的问题。在香农熵的定义中,如果p i→0,则信息增量ΔI(p i)→∞;当p i=0时,ΔI(p i)=-log2(p i)没有定义[12]。因此,为了解决计算过程中出现不收敛的现象,用e1-pi代替能起到较好的效果,并且能提高计算精度。则指数熵表达式为
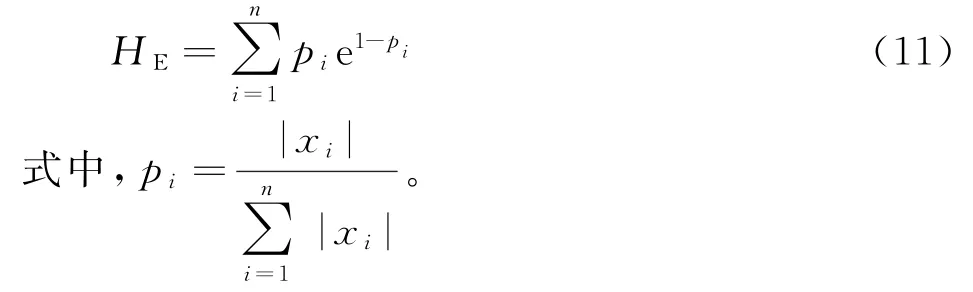
范数熵在描述不同脉内调制方式的雷达辐射源信号的频谱形状、能量分布和集中程度上有较好的效果,因此,本文用它来定量描述信号的能量分布情况,信号能量分布越分散,范数熵越大。下面给出范数熵的定义[13]:

式中,1<R<2,本文中取R=1.5。
2.2 三维熵特征性能分析
为了对三维熵特征的性能进行分析,本文对仿真的8类雷达辐射源信号的参数进行如下设置:8类信号的脉宽均为20μs,采样频率均为120 M Hz,最大延迟数kmax=240,其他调制参数设置如表1所示。

表1 8类雷达辐射源信号参数
在信噪比为5,10,15和20 d B时,首先分别求出8类雷达辐射源信号自相关函数的三维熵特征,每类信号进行蒙特卡洛仿真产生100个,然后求出每一类信号在对应信噪比时的三维熵均值和方差,如图3和图4所示。图3和图4中1~8分别表示CW,LFM,FSK,BPSK,QPSK,LFM-BPSK,FSK-BPSK和NLFM信号。
由图3可知,当某个熵不足以区分8类雷达辐射源信号时,可以结合其他熵进行分析,总体而言,8类雷达辐射源信号自相关函数的三维熵特征存在差异,即具有较好的分离性。由图4可知,香农熵方差小于0.01,指数熵方差的数量级小于-5,范数熵方差小于2.5,说明8类雷达辐射源信号自相关函数的三维熵特征具有较好的稳定性,且稳定性随着信噪比的增大而增大。
综上分析,三维熵特征具有较好的分离性和稳定性,则本文对雷达辐射源信号进行分选的特征参数即选为三维熵特征H:


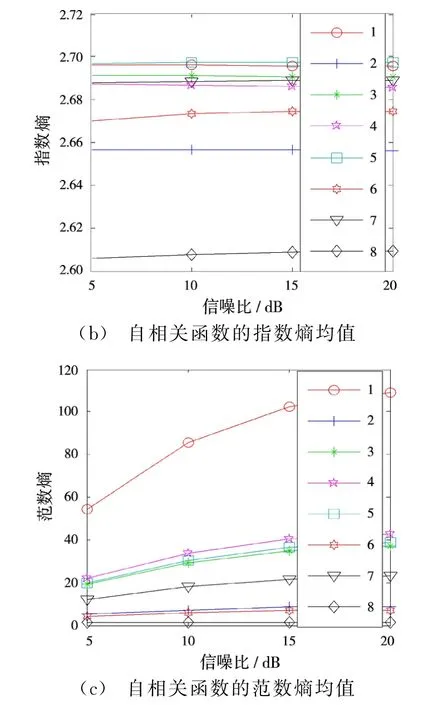
图3 8类雷达辐射源信号的三维熵均值
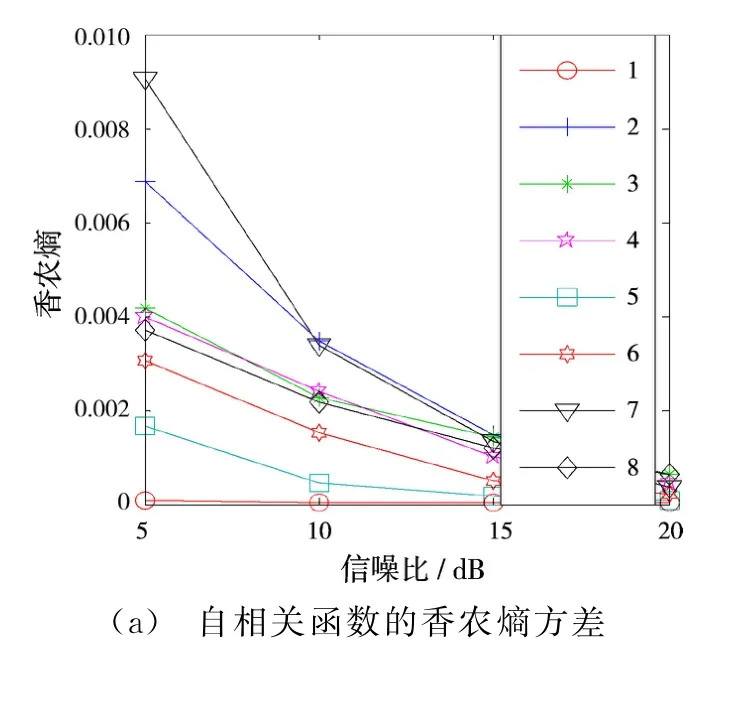

图4 8类雷达辐射源信号的三维熵方差
3 分选实验
为了对特征参数提取方法的有效性进行验证,本文采用KFCM算法进行分选实验。KFCM算法是一种无监督的分类方法,是在没有先验知识的情况下,利用待处理数据的内在规律和联系对其进行分类的过程,在数据分析和图像分割等方面具有广泛的应用。KFCM算法参数设置如下:初始聚类数目c0=2,最大可能类别数cmax=8,迭代次数为50,停止条件ε≤0.001,核函数为高斯径向基核。
3.1 雷达辐射源信号的周期性对分选性能的影响
为了考察接收信号的周期性对分选性能的影响,本文主要对信号周期T=50,100,…,1 000情况下的分选准确率进行分析。在5,10,15和20 dB信噪比条件下,以最大延迟数kmax=240为例,得到8类信号在不同信号周期时的平均分选准确率,如图5所示。

图5 分选准确率与信号周期的关系
由图5可知,在信噪比为20 dB时,分选准确率始终为100%,不受雷达辐射源信号周期性的影响;在信噪比为5,10和15 d B时,随着信号周期的变化,分选准确率出现上下波动,且波动的方差分别为0.084 8,0.017 9和0.002 3,可见噪声越大,波动越大。总体而言,信号周期性对分选准确率存在一定的影响。
3.2 自相关函数的最大延迟数对分选性能的影响
为了考察自相关函数的最大延迟数对分选性能的影响,本文主要对最大延迟数kmax=120,240,…,2 280情况下的分选准确率进行分析。在5,10,15和20 d B信噪比条件下,以信号周期T=100为例,得到8类信号在不同最大延迟数时的平均分选准确率,如图6所示。

图6 分选准确率与最大延迟数的关系
由图6可知,当信噪比为15 dB和20 dB时,分选准确率始终为100%,不受自相关函数的最大延迟数的影响;当信噪比为5 dB和10 dB时,随着最大延迟数的变化,分选准确率出现上下波动,且波动的方差分别为1.871 3和0.104 7,可见噪声越大,波动越大。总体而言,自相关函数的最大延迟数对分选准确率存在一定的影响。
3.3 每类雷达辐射源信号的分选情况
为了具体地分析每类雷达辐射源信号的分选情况,在5,10,15和20 d B信噪比条件下,以信号周期T=100、最大延迟数kmax=240为例,得到8类雷达辐射源信号的分选准确率,如表2所示。

表2 8类雷达辐射源信号的分选准确率 (%)
由表2可知,当信噪比为15 dB和20 dB时,8类雷达辐射源信号的分选准确率均为100%;随着信噪比的降低,有些信号的分选准确率有所下降,由图3观察可知,当信噪比为10 d B时,BPSK和FSK-BPSK的三维熵特征存在小部分交叠,导致这2类信号的分选准确率略有下降,其他信号的分选准确率均为100%;当信噪比为5 d B时,LFM、BPSK和FSK-BPSK的三维熵特征交叠进一步增加,分选准确率也进一步下降,但最低仍能达到91%,总体令人满意。
3.4 不同分选方法比较
为了进一步验证本文分选方法的有效性,在同等条件下分别采用本文方法、文献[3]方法和文献[4]方法对8类辐射源雷达信号进行分选实验,实验结果如图7所示(1,2,3分别表示本文方法、文献[3]方法、文献[4]方法)。由图7可知,本文方法的总体分选准确率要高于其他两种方法,并且本文方法是对接收的时域信号直接分析自相关函数后,提取三维熵特征进行分选;文献[3]方法是对接收的信号进行频域变换和去噪预处理后,提取复杂度特征进行分选;文献[4]方法是在模糊函数三维空间进行子空间的划分后,求取相像系数进行分选,计算量都要大于本文方法。通过以上的分析,进一步体现了本文方法分选准确率高、计算量小和易于工程实现的优点,且在较低的信噪比下,仍然可以较好地实现对信号的分选。
4 结束语

图7 不同方法的分选准确率比较
为了解决当前雷达辐射源信号分选方法准确率不高和对噪声敏感的问题,本文提出一种基于自相关函数三维熵特征的分选方法。根据自相关函数对噪声不敏感的特点,对接收到的雷达辐射源信号首先分析其自相关函数,然后根据熵对信号无序状态具有较强的刻画能力,进一步提取自相关函数的三维熵特征,以达到降维和提高分选效率的目的,最后基于KFCM算法实现对8类雷达辐射源信号的分选。理论分析和仿真实验表明,不同雷达辐射源信号的自相关函数区别较大且对噪声不敏感,三维熵特征具有较好的分离性和稳定性,虽然雷达辐射源信号的周期性和自相关函数的最大延迟数对分选性能均存在一定的影响,但新方法在较低的信噪比下对不同调制样式的雷达辐射源信号仍然具有较高的分选准确率,且易于工程实现,具有一定的参考价值。
[1]NELSON D.Special Purpose Correlation Functions for Improved Signal Detection and Parameter Estimation[C]∥IEEE International Conference on Acoustics,Speech and Signal Processing,Minneapolis,MN:IEEE,1993:73-76.
[2]NISHIGUCHI K,KOBAYASHI M.Improved Algorithm for Estimating Pulse Repetition Intervals[J].IEEE Trans on AES,2000,36(2):407-421.
[3]韩俊,何明浩,朱振波,等.基于复杂度特征的未知雷达辐射源信号分选[J].电子与信息学报,2009,31(11):2552-2556.
[4]陈昌孝,何明浩,徐璟,等.基于模糊函数相像系数的雷达辐射源信号分选[J].电波科学学报,2014,29(2):260-264.
[5]HAN Jun,HE Minghao,MAO Yan,et al.A New Method for Recognizing Radar Radiating-Source[C]∥International Conference on Wavelet Analysis and Pattern Recognition,Beijing:IEEE,2007:1665-1668.
[6]CHEN Changxiao,HE Minghao,XU Jing,et al.A New Method for Sorting Unknown Radar Emitter Signal[J].Chinese Journal of Electronics,2014,23(3):499-502.
[7]张学恒.基于时间序列分析的结构损伤识别研究[D].重庆:重庆大学,2014.
[8]郭松.基于时间序列分析的基坑沉降监测数据分析研究[D].上海:华东理工大学,2015.
[9]王天佐,王常明,姚爱军,等.基于时间序列的地铁横通道拱顶沉降预测[J].现代隧道技术,2016,53(3):74-80.
[10]谢中凯.信息熵理论在混凝土结构损伤动力识别中的应用研究[D].杭州:浙江大学,2013.
[11]李靖超.基于三维熵特征的雷达信号识别[J].上海电机学院学报,2015,18(3):136-140.
[12]蒋莹,何明浩,郁春来,等.基于熵理论的间歇采样转发干扰识别方法[J].现代防御技术,2016,44(3):105-108.
[13]徐璟,何明浩,陈昌孝,等.雷达辐射源特征参数提取算法复杂度分析[J].中国电子科学研究院学报,2013,8(1):43-47.

