浅谈电路分析中的特勒根定理
曹家琪 孙杨
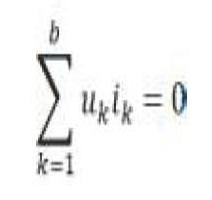

摘要:本文主要通过对特勒根定理的简析及在题目中的使用方法的阐述,以表明其应用的普遍性。
关键词:特勒根定理;功率守恒;似功率守恒;互易定理
中图分类号:TP311 文献标识码:A 文章编号:1009-3044(2018)31-0217-02
Discussion on the Tellegens Theorem in Circuit Analysis
CAO Jia-qi, SUN Yang
(Nanjing University of Posts and Telecommunications Bell Honors School, Nanjing 210023, China)
Abstract: This article mainly explains the Tellegens Theorem and its use in the questions, so as to show its universality.
Key words: Tellegens Theorem; Conservation of the Power; Conservation of the Similarpower; Reciprocity Theorem.
特勒根定理是一个分析任何集总参数网络普遍适用的有效定理,也是电路分析网络定理中的一个重点与难点,不仅在网络理论的研究中有着广泛的应用,而且对电路设计的实践和优化也有着重要的意义。故本文将对特勒根定理进行深入的讨论,以便读者更清晰地了解其中的有关内容。
1 特勒根定理的两种表现形式
1.1 特勒根第一定理
任意一个具有b条支路、n个节点的集总参数网络,设它的各支路电压和电流分别为uk和ik,其中k = 1 , 2 , 3 … b,且各支路电压和电流取关联参考方向,则有
上式中的每一项是同一支路电压和电流的乘积,表示的是支路的吸收功率,因此特勒根第一定理表达的是功率守恒。
1.2 特勒根第二定理
上式中的每一项是一个网络中的支路电压和另一个网络相应支路的电流的乘积,具有功率的量纲,称之为似功率,因此特勒根第二定理表达的是似功率守恒。
1.3 说明
①特勒根定理是基尔霍夫定律的结果,它具有和基尔霍夫定律本身一样的普遍性,适用于任何性质(线性、非线性、时不变、时变等)的电路。
②对于特勒根第二定理而言,不能用功率守恒来解释,它仅表明在两个具有相同拓扑结构的电路中,一个电路的支路电压和另一个电路的支路电流,或者是同一电路在不同时刻的相应的支路电压和支路电流所必须遵循的数学关系。虽具有功率的量纲,但并无具体的物理意义。
③无论是特勒根第一还是第二定理,其实质均是功率守恒。
④运用特勒根定理解题时,为方便将对应支路的电压和电流相乘或交叉相乘,应将各个支路的电压和電流依次排列,这样也可以避免漏写和错位。同时应该注意对应的支路电压和支路电流必须满足关联参考方向(否则公式中加负号)。
⑤注意运用特勒根定理时对端口支路的处理。若端口开路,则端口支路的电流为零;若端口短路,则端口支路的电压为零。
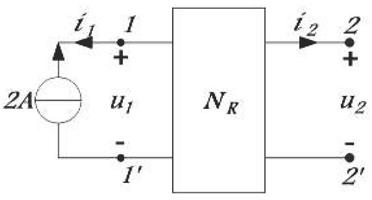
2 特勒根定理的应用
从这道题目的两种解法可以看出,第二种解法明显技巧性更强,但计算量就相对较小,而第一种解法的思考量小,但计算时要注意细节方面的处理,如电流与电压的关联与否,往往一个点判断错误计算结果就会出现偏差。故在选取方法时要仔细斟酌,使用合适自己的方法。
而对于第一种直接使用特勒根定理的方法而言,可以先将各个端口的电流和电压取为关联参考方向,然后直接列写特勒根定理的表达式,即(*)式,可以不用从定理最初的表达式推至(*)式,同时,在将已知参数代入表达式的时候,若该参数与先前选定的电压、电流的方向相同,则取正号,否则取负号。
利用特勒根定理证明互易定理
注意到特勒根第二定理即似功率守恒定理,其所提供的两个等式包含了两个网络的4b个变量,因此,如果直接应用该定理求解网络,则必须给出4b - 2 个网络变量,否则网络的解就不会唯一。这给定理的实际应用带来了困难,尤其是变量个数较多的情况下,方程的求解就更加复杂;但是,如果给定的网络满足某些特殊条件,应用特勒根定理,往往可以得出一些有益的结论,如2.1的题解中的第二种方法所提到的互易定理。
3 结语
特勒根定理的应用十分广泛,适用于许多电路,无论其是否包含非线性元件、是否是稳恒电路。而且对电流电压做线性变换不影响特勒根定理的成立。
另外,在应用特勒根定理解题时,如若题中所给网络不为纯电阻网络,例如含有受控源等,则不能直接列写(*)式。原因 在于此时的网络中的约束关系不再是简单的VCR关系,这也就导致了除已知支路外的网络,即被封住的网络中的支路电压与对应支路的电流的乘积之和与支路电流与对应支路的电压的乘积之和不再相等,则不能被约去,因此不能推至(*)式。
参考文献:
[1] 邱关源,罗先觉.电路[M].5版.北京:高等教育出版社,2006.
[2] 刘崇新,罗先觉.电路(第五版)学习指导与习题分析[M].5版.北京:高等教育出版社,2006.
[3] 张宇飞,于舒娟.电路分析辅导与习题详解[M].北京:北京邮电大学出版社,2006.
[4] 于舒娟,史学军.电路分析典型题解与分析[M].北京:人民邮电出版社,2004.

