热塑性复合材料自动铺放过程中温度场研究
宋清华,肖 军,文立伟,王显峰,范珏雯,石甲琪
(南京航空航天大学 材料科学与技术学院,南京 210016)
复合材料低成本制造技术是目前国际上复合材料技术领域关注的核心问题之一,而复合材料自动铺放技术是欧美发达国家近30年来广泛发展和应用的低成本自动化制造的典型代表[1-2]。自动铺放技术的加工对象主要为热固性复合材料和热塑性复合材料[3-4]。热固性复合材料自动铺放技术结合“热压罐”技术已广泛应用于飞机制造领域(图1(a))。热塑性复合材料以韧性高、重复加工性好及防火性能强使其成为航空结构件的理想材料,如空客A340/A380飞机机翼前缘应用玻璃纤维增强的聚苯硫醚复合材料,ICI公司利用50%长玻纤增强尼龙66制造飞机上的阀门,代替原来使用的酚醛石棉复合材料,满足飞机阀门在宽的温度范围内与燃料长期接触也能保持其性能和形状的要求[5-6]。而热塑性复合材料与自动铺放技术相结合,采用“原位固结”技术(图1(b)),与“热压罐”技术相比,“原位固结”技术不受加工场地和零件大小与形状的限制,且构件在铺放过程中一次成型,加工效率高,因此热塑性复合材料自动铺放技术将会是未来生产航空航天复合材料构件的重要技术[7-8]。然而由于热塑性复合材料对温度的敏感性,在铺放过程中其内部的温度历程非常复杂,不同的温度梯度会引起复合材料内部热应力和热变形,进而对成型构件的力学性能有很大的影响,因此对热塑性复合材料自动铺放成型过程中的温度场分布进行研究具有重要的理论意义与实用价值。

图1 复合材料自动铺放设备(a)热固性复合材料自动铺放设备;(b)热塑性复合材料自动铺放设备Fig.1 AFP system for composites (a)AFP system for thermoset composites;(b)AFP system for thermoplastic composites
热塑性复合材料自动铺放过程中的温度场的研究在国外早已引起重视,目前已有比较多的数学模型和分析模型预测热塑性复合材料自动铺放过程中的温度场分布。根据热力学第一定律,建立热传递模型,模型的维数通常根据热传递方向分为一维、二维、三维三类,根据加热方式的不同及模型周围环境确定热传递模型的边界条件和初始条件。由于边界条件比较复杂,一般采用有限元软件进行建模求解[9]。John等[10]仅考虑热量沿预浸料厚度方向传递,忽略沿长度和宽度方向的传递,对热塑性复合材料自动铺放过中的温度场建立了一维热传递模型,并进行铺放实验以验证模型的正确性。Grove[11]对激光辅助加热APC-2型预浸料自动铺放成型过程建立二维热传递模型,其采用一个固定的坐标系统,研究激光能量与铺放速率之间的关系。Tumkor等[12]利用有限差分法建立热塑性复合材料自动铺放过程中温度场数学模型,并给出温度场随时间变化的解析解。Noha等[13]利用ABAQUS建立三维有限元模型对热塑性复合材料自动铺放过程进行瞬态分析,同时对有限元分析结果与实验结果之间的误差给出相应分析。目前国内对热塑性复合材料自动铺放过程中温度场的研究比较少,天津工业大学李志猛等[14-15]使用半无限大固体的对流传热模型对铺放过程中的热对流和热传导进行分析,建立一维热传递数学模型,利用ANSYS对铺放过程中热量的瞬态热传递进行了动态仿真。哈尔滨工业大学李玥华等[16]从整体角度出发,对热塑性复合材料自动铺放成型各环节进行建模,同时考虑各环节之间存在的联系,确定铺放工艺参数。但国内关于热塑性复合材料自动铺放过程中二维热传递模型动态仿真及原位固结过程中温度场在线测量仍缺乏研究。
本工作通过建立热塑性复合材料自动铺放过程中温度场二维数学模型,利用ANSYS软件对整个铺放过程热量的瞬态热传递进行仿真,研究铺放过程中温度场分布及其随时间的变化。同时借助热塑性复合材料自动铺放平台构建温度场在线测量系统,采集和存储自动铺放过程中黏合区域的温度峰值及铺层的温度场分布。
1 热塑性复合材料自动铺放过程中温度场数学模型
热塑性复合材料自动铺放过程中,预浸料在热源加热及压辊压力作用下被铺叠到底层预浸料上,实现复合材料自动铺放成型。如图2所示,整个铺放过程是三维的,但通常加热源的加热范围要比预浸料的宽度大,因此本工作认为热量在预浸料宽度方向上的传递是处处相等的,根据热力学第一定律,建立沿预浸料长度和厚度方向的二维热传递模型,模型的热传递方程为:
(1)
式中:ρ为预浸料的密度;c为预浸料的比热容;T为加热源的温度;τ为时间;kx为预浸料沿着x方向即纤维方向的导热系数;ky为预浸料沿着y方向即铺层厚度方向的导热系数。

图2 热塑性复合材料自动铺放示意图Fig.2 Schematic diagram of AFP for thermoplastic composites
1.1 几何模型
图3为热塑性复合材料自动铺放过程的二维几何模型,x轴正方向沿模具底部水平向右,与铺放成型的方向一致,y轴正方向沿着铺层厚度方向垂直向上。d为单层预浸料的厚度,y1为铺层厚度,y2为模具厚度,x1为黏合点距原点的距离,l1和l2表示压辊与预浸料的接触长度,由于压辊压力作用使预浸料与铺层基层产生变形,因此压辊中心的x坐标与黏合点的x坐标不重合[17]。l3表示热源的加热长度,θ为热源加热角度。

图3 自动铺放过程二维几何模型Fig.3 Model of two-dimensional geometry for AFP
1.2 边界条件
为求解公式(1),首先必须确定热塑性复合材料中自动铺放过程中二维热传递模型的边界条件。自动铺放开始前,假设模具的表面温度为Ttool以及预浸料的表面温度为Ttape。因此,当τ=0时,
在面Γ1,Γ2,Γ4上,
T(x,y)=Ttape
(2)
在面Γ10,Γ11,Γ12上,
T(x,y)=Ttool
(3)
铺放成型过程中,根据傅里叶定律及牛顿冷却公式对热传递模型边界条件描述如下。
在面Γ5,Γ13上,预浸料与空气进行自然对流换热,
(4)
(5)
在面Γ8,Γ9上,铺层与空气进行自然对流换热,
(6)
(7)
式中:n表示传热表面的法线方向;h1为自然对流条件下预浸料表面传热系数;T∞为环境温度。
由于自动铺放设备中的压辊与模具都是由钢制作而成,其传热系数与预浸料相比是非常大的,在铺放过程中,把压辊及模具作为冷却源。因此,在面Γ3上,
(8)
式中:hr为压辊的对流换热系数;Tr为铺放过程中的压辊表面温度。
在面Γ10,Γ11,Γ12上,
(9)
(10)
(11)
式中:ht为模具的对流换热系数;Tt为铺放过程中的模具表面温度。
本实验选择热风枪为加热设备,因此热源是高温气体,在面Γ6,Γ7加热区域,
(12)
式中:h2为强制对流条件下预浸料表面传热系数;Thot为高温气体温度。
自动铺放成型过程中,热量的传递不仅有热传导和热对流,还存在热辐射,但辐射传热系数远小于对流传热系数,为便于求解,在分析中忽略辐射传热。
2 基于ANSYS铺放过程的有限元建模与求解
热塑性复合材料自动铺放成型过程中,在热源的作用下,每一铺层及各铺层间都会存在不同的结晶状态及温度梯度,铺层温度场的分布是随时间不断变化的,因此铺放过程中的温度场是一种非稳态传热过程,本工作选用ANSYS有限元分析软件中的Thermal模块对上述问题进行瞬态热分析。
2.1 有限元控制方程
在有限元分析过程中,根据能量守恒原理,将温度场导热微分方程转化为等效的瞬态传热有限元控制方程:
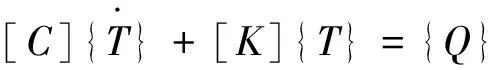
(13)
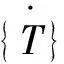
根据公式(13),在给定材料属性、边界条件的情况下,依据有限元的思想进行迭代求解,可以计算出铺层中任何一点的温度。一般进行温度场有限元分析时,二维模型使用四边形或三角形单元进行划分,本实验选用PLANE13单元作为网格划分的单元类型,该单元为二维耦合场单元,在满足二维瞬态热分析的同时,还能在热场和结构场之间实现耦合,便于后续对铺放过程中的热应力进行分析。
2.2 输入参数的确定
本实验采用玻璃纤维增强聚丙烯复合材料,聚丙烯熔点为150℃,热分解温度为350℃。由于聚丙烯的材料性能是非线性的,其热导率、比热容、密度都随温度变化而变化[18]。因此,GF/PP的材料性能也是非线性的,其热性能参数随温度的变化如图4所示。

图4 GF/PP热性能参数随温度的变化(a)热导率随温度的变化;(b)比热容随温度的变化;(c)密度随温度的变化Fig.4 Profile of the thermal parameters with the temperature variation for GF/PP(a)profile of the thermal conductivity with the temperature variation;(b)profile of the special heat capacity with the temperature variation;(c)profile of the density with the temperature variation
在对流传热中,大空间自然对流换热的实验准则关系式具有下列通用形式:
(14)
式中:Num为努赛尔准则;Gr为格拉晓夫准则;Pr为普朗特准则;C和n由换热面形状及Gr共同决定;m表示定性温度;取边界层平均温度为tm,它定义为:
(15)
式中:tw为对流换热表面温度;tf为流体温度。
对流换热表面传热系数h的计算公式如下:
(16)
式中:λm为导热系数;l为自然对流区域的长度。
经计算得到GF/PP在不同温度下自然对流换热表面传热系数如表1所示。
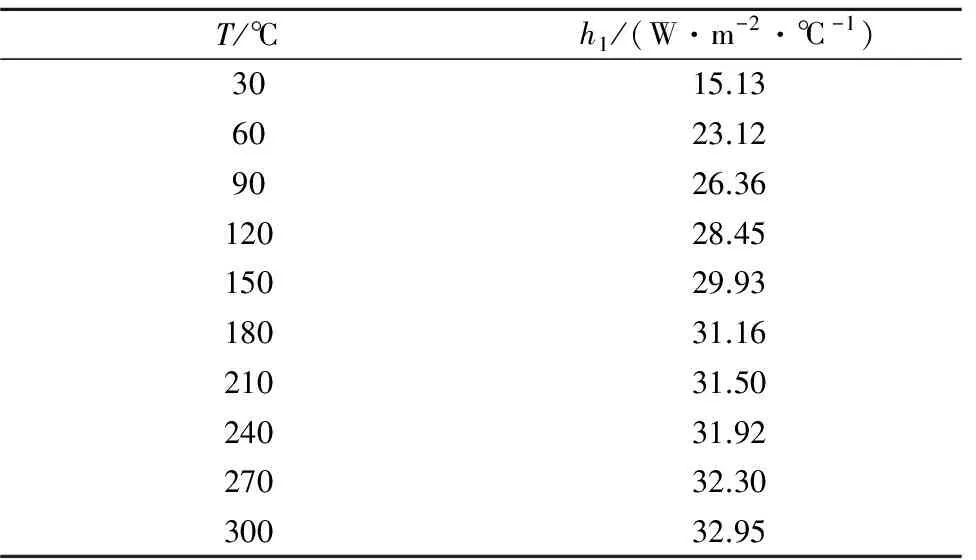
表1 GF/PP在不同温度下自然对流换热表面传热系数Table 1 Coefficient of heat transfer at surface of GF/PP under free convection at different temperatures
在自动铺放过程中,热气载荷直接施加在面Γ6,Γ7区域,在此区域强制对流热传导中,首先需由雷诺准则确定努塞尔数:
(17)
式中:Re为雷诺准则;u∞为热气流速;υ为热气动力黏度。
当Re>5×105时,
Num=0.664Re0.5Pr1/3
(18)
当5×105≤Re<107时,
Num=(0.037Re0.8-871)Pr1/3
(19)
结合公式(15),(16),计算出面Γ6,Γ7区域内平均温度在300~600℃范围内热气流速u∞=60m/s时的表面传热系数如表2所示。

表2 GF/PP在不同温度下强制对流换热表面传热系数Table 2 Coefficient of heat transfer at surface of GF/PP under forced convection at different temperatures
2.3 自动铺放过程的有限元建模
本实验使用的预浸料单层厚度为0.29mm,铺放长度为300m,模具厚度20mm,在ANSYS中创建如图5所示进行6次铺放的有限元模型,因为分析的重点在于铺层部分,所以对铺层进行等间距网格划分,而对模具采用不均匀网格划分。表3为有限元模型尺寸及边界条件参数。

图5 温度场有限元分析模型网格划分Fig.5 Finite element model meshing for temperature field
自动铺放过程中,铺层自身形态以及施加载荷的分布是随着时间不断变化的。在铺层逐步完成自下向上、由左至右生长的同时,热源施加的热载荷沿着铺层长度方向以一定速率均匀移动,因此在有限元分析时,采用生死单元技术及循环加载技术模拟一直变化的模型,其求解流程如图6所示。

表3 有限元模型尺寸及边界条件Table 3 Finite element model size and boundary conditions

图6 温度场求解流程图Fig.6 Flow chart of the temperature field solution
单元的生与死被定义为一种非线性的状态变化,将生死单元“杀死”,实际上其导热系数被设定为极小值;当生死单元被激活时,其又被恢复为具有一定导热系数的单元。在建立有限元模型后,对模型各节点施加初始温度约束,并将所有铺层单元杀死,根据图6所示的求解流程,每增加一个载荷步,激活要进行铺放的铺层单元,使预浸料被实时铺叠到基体中,同时删除上一载荷步中施加的载荷并在新激活的单元节点上施加热载,从而实现铺层实时生长及热源的移动。
2.4 自动铺放过程的有限元模拟结果分析
图5所示的模型总长度为0.3m,在有限元模型铺层中间,即距模具左侧0.15m处,第1~6层节点编号分别为268~272,100。当热源未加热到所选节点时,此节点处于自然对流边界;当热源运动到所选节点上方时,此节点处于强制对流边界条件。有限元仿真过程中通过选取的节点记录铺放成型过程中每层预浸料铺层温度场随时间的变化规律。当热气温度为500℃,铺放速率为0.6m/min时,节点温度随时间的变化如图7所示。图7(a)为铺完6层后第1层预浸料温度随时间变化曲线,图中共出现6次波峰,第1个波峰代表铺放第1层时,压辊移动到模具中间,节点268的温度值。由于模具的吸热量比较大,此节点的温度没有大幅度增长;第2个波峰代表铺放第2层时,节点268的温度值,此时热源作用于第1层预浸料和第2层预浸料之间,因此如图7(b)所示,第1层的第2个波峰与第2层的第1个波峰基本重叠,这表明铺放时相邻两层间的温度非常接近。此时由于第1层预浸料的阻热作用,同时上一层铺放时由于温度累积使模具吸热量减小,因此节点268温度得以迅速上升。当铺放第3至第6层时,热源不再直接作用于第1层,第1层的温升全部依赖于其他层的热传导,因此第1层的第3至第6个波峰均没第2个高且逐渐降低。不过由于热量累积,铺层整体的温度逐渐上升,如图7(b)所示。

图7 热气温度500℃、铺放速率0.6m/min铺层温度随时间变化曲线(a)铺放过程中第1层温度场变化;(b)铺放过程中所有铺层温度场变化Fig.7 Graphs of the temperature field changes at heat temperature of 500℃ and processing speed of 0.6m/min(a)temperature field changes at the first layer;(b)temperature field changes at all layers
3 实验验证与分析
为实时测量铺放过程中黏合区域温度峰值及铺层经历的温度历程,需构建自动铺放过程中温度场在线测量系统。一个完整的自动铺放温度在线采集系统包括自动铺放平台、温度采集部分、信号处理部分、数据显示及存储部分,如图8所示。

图8 自动铺放温度在线采集系统Fig.8 Temperature acquisition system for the AFP
本实验采用热电偶作为温度采集部分的温度测量元件,采集的温度值经西门子Step-300 PLC信号处理后,由西门子触摸屏Smart 700显示并存储温度值,其原理图如图9所示。

图9 温度采集系统原理图Fig.9 Diagram of the temperature acquisition system
整个温度采集系统以PLC为信号处理中心,通过Profibus-DP现场总线与西门子触摸屏Smart 700建立通信网络,系统以触摸屏基于WinCC flexible软件编写的人机交互界面,实时更新并存储铺层温度。铺放开始前,先把热电偶F固定在模具中间位置,当第1层铺放完成后,为降低因植入热电偶而造成铺层厚度的增加,选择热电偶沿纤维方向交错排列,完成6次铺放,共植入6只热电偶,如图10所示。

图10 温度采集系统实物图Fig.10 Picture of the temperature acquisition system
当热气温度为500℃,铺放速率为0.6m/min时,热电偶测量的铺放第6层时温度场变化如图11所示,图12为同时使用红外成像仪拍摄的铺放第4层时温度场画面。通过对比图7可以看出,自动铺放过程中温度场在线测量系统的测量结果与有限元仿真结果的基本吻合,但是在黏合区域,测量结果与仿真结果相对差距比较大,原因有两方面,首先,由于测量元件热电偶属于接触式测温法,相对于红外传感器,其灵敏度及精度略低,而铺放过程铺层温度场是不断变化的,属于非稳态瞬间变化过程,因此热电偶跟不上铺层的温度变化速率而出现测温滞后,其测量结果就低于红外成像仪的测量的结果及有限元仿真结果;其次,有限元仿真时,在黏合区域边界条件过于简化,也使得仿真结果高于热电偶的测量结果。
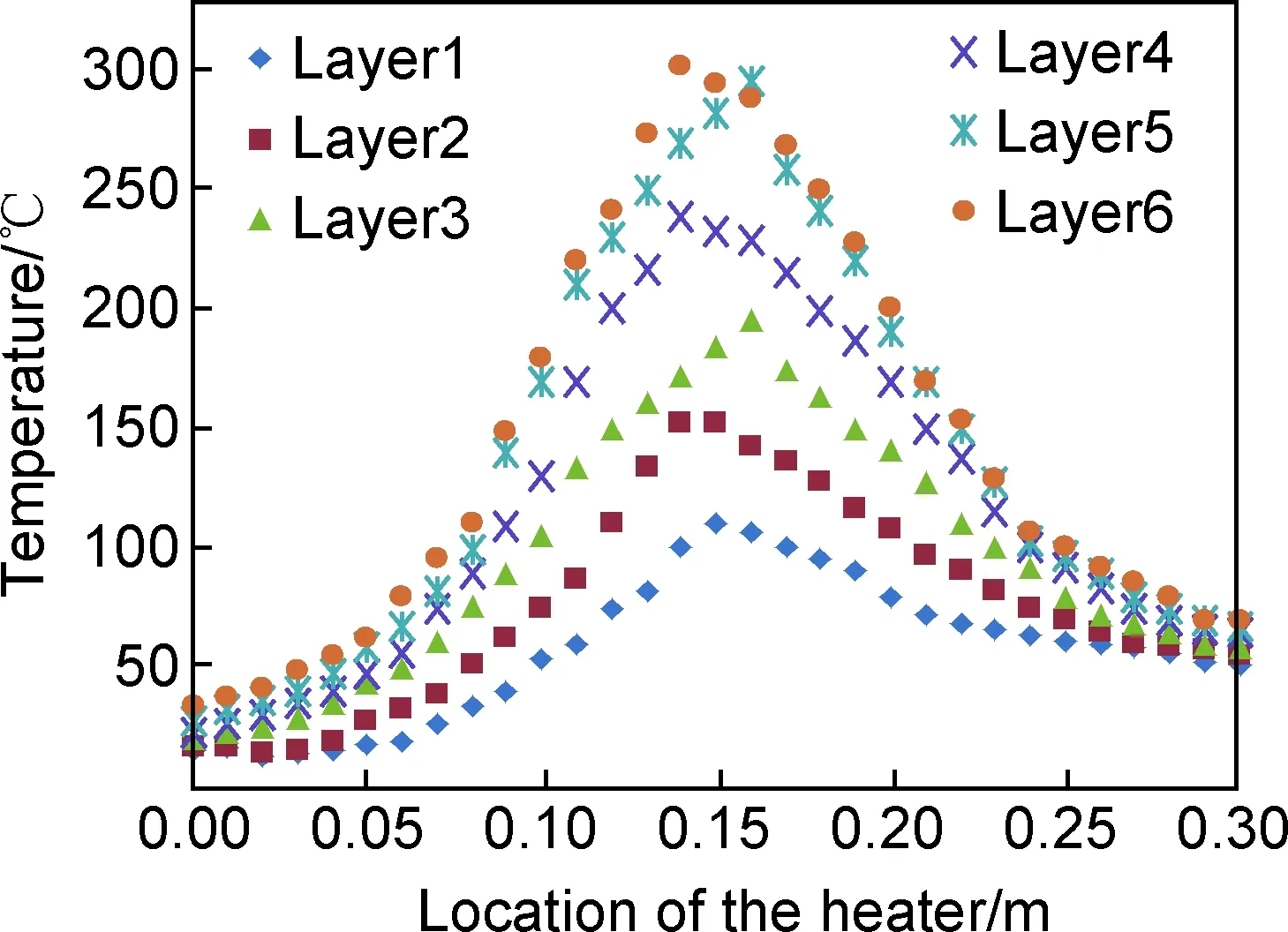
图11 热电偶测量铺放第6层时温度场变化Fig.11 Temperature field changes at the sixth layer measured by thermocouples

图12 铺放第4层时红外成像仪拍摄温度场画面Fig.12 Temperature field changes at the fourth layer measured by infrared thermal imager
当铺放速率固定为0.6m/min,将加热温度从300℃升高到600℃时,各铺层温度峰值随加热温度变化规律如图13所示。从图中可以看出,随着热气温度的升高,每层峰值温度逐渐增加,且热气温度越高,铺层间峰值温度差越大,而热电偶测量结果与仿真结果相差越小;随着铺层数的增加,铺层间的峰值温度差越小;当热气温度为350℃时,第1层的峰值温度没有达到树脂基体的熔点,而当热气温度为550℃时,第6层的峰值温度已达到树脂基体的热分解温度,因此,当铺放速率为0.6m/min时,热气加热温度为400~500℃。

图13 热气温度对铺层峰值温度的影响Fig.13 Influence of the temperature of hot gas on all layers’ peak temperature
加工速率对生产效率具有重要意义,铺放速率越快,生产效率越高,而热塑性复合材料自动铺放过程中热气温度越高,铺放速率越快,因此选择热气温度为600℃,将铺放速率从0.6m/min升高到1.5m/min时,各铺层温度峰值随铺放速率变化规律如图14所示。

图14 铺放速率对铺层峰值温度的影响Fig.14 Influence of the speed of roll on the all layers’ peak temperature
从图14可以看出,随着铺放速率的加快,每层峰值温度逐渐降低,且铺放速率越快,铺层间峰值温度差越小,而热电偶测量结果与仿真结果相差越大;随着铺层数的增加,铺层间的峰值温度差越小;当铺放速率大于1.2m/min时,第1层的峰值温度没有达到树脂基体的熔点,因此当选择热气温度为600℃时,最快铺放速率为1.2m/min。
4 结论
(1)基于自动铺放过程中二维温度场数学模型及热传递边界条件,建立温度场动态有限元模型,对铺放过程中瞬态热传递进行了仿真,得到铺放过程中铺层温度场随时间的变化;同时构建温度场在线测量系统,对铺层温度进行在线采集与存储。通过对比,测量结果与有限元仿真结果基本吻合,证明了仿真模型的正确性。
(2)在铺放过程中,每一层预浸料的温度曲线出现多个峰值,且随着热气温度的升高,每层峰值温度逐渐增加,热气温度越高,铺层间峰值温度差越大,热电偶测量结果与仿真结果相差越小;随着铺放速率的加快,每层峰值温度逐渐降低,为满足成型要求,当热气温度最高为600℃时,最大铺放速率为1.2m/min。
(3)虽然热气温度越高,铺放速率越快,但加热温度越高,树脂基体降解的可能性增大。因此,为得到最优加工参数,需对铺放过程中的热应力进一步研究,获得性能更优自动铺放成型的热塑性复合材料构件。
[1] 肖军, 张建宝, 李勇, 等. 自动铺带技术研究现状[J]. 航空制造技术, 2008(25): 126-128.
XIAO J, ZHANG J B, LI Y, et al. Research status of automatic tape-laying technology[J]. Aeronautical Manufacturing Technology, 2008(25): 126-128.
[2] 肖军, 李勇, 文立伟, 等. 树脂基复合材料自动铺放技术进展[J]. 中国材料进展, 2009, 28(6): 28-32.
XIAO J, LI Y, WEN L W, et al. Progress of automated placement technology for polymer composites[J]. Materials China, 2009, 28(6): 28-32.
[3] 韩振宇,孙守政,付云忠,等.热塑性FRP自动铺放成型缺陷的多尺度研究进展[J].材料工程,2017,45(7):118-127.
HAN Z Y,SUN S J,FU Y Z,et al.Multi-scale research progress of manufacturing defects for thermoplastic FRP fabricated by automated fiber placement[J].Journal of Materials Engineering, 2017,45(7):118-127.
[4] 宋清华, 文立伟, 严飙, 等. 热塑性树脂基复合材料自动铺带技术[J]. 航空制造技术, 2011(15): 42-44.
SONG Q H, WEN L W, YAN B, et al. Automated tape laying technology of thermoplastic and resin-based composites[J]. Aeronautical Manufacturing Technology, 2011(15): 42-44.
[5] 张婷. 高性能热塑性复合材料在大型客机结构件上的应用[J]. 航空制造技术, 2013(15): 32-35.
ZHANG T. Applications of high performance thermoplastic composites for commercial airplane structural component[J]. Aeronautical Manufacturing Technology, 2013(15): 32-35.
[6] 宋清华, 肖军, 文立伟, 等. 玻璃纤维增强热塑性塑料在航空航天领域中的应用[J]. 玻璃纤维, 2012(6): 40-43.
SONG Q H, XIAO J, WEN L W, et al. Applications of glass fiber reinforced thermoplastics in aerospace sector[J]. Fiber Glass, 2012(6): 40-43.
[7] 迪力穆拉提·阿卜力孜,段玉岗,李涤尘,等. 树脂基复合材料原位固化制造技术概述[J].材料工程,2011(10): 84-90.
ABULIZI D, DUAN Y G, LI D C, et al. Overview ofin-situcuring manufacturing technology for resin matrix composites[J]. Journal of Materials Engineering, 2011(10): 84-90.
[8] 谢薇. 新型热塑性复合材料设计概念及其自动化生产[J].玻璃钢,2010(4): 18-21.
XIE W. New thermoplastic composites design concepts and their automated manufacture [J]. Reinforced Plastics, 2010(4): 18-21.
[9] 韩振宇,李玥华,富宏亚,等. 热塑性复合材料纤维铺放工艺的研究进展[J]. 材料工程, 2012(2): 91-96.
HAN Z Y, LI Y H, FU H Y, et al. Thermoplastic composites fiber placement process research[J]. Journal of Materials Engineering, 2012(2): 91-96.
[10] JOHN T, GILLESPIE J W. Modeling ofinsitustrength development for the thermoplastic composite tow placement process[J]. Journal of Composite Materials, 2006, 40(16): 1487-1506.
[11] GROVE S M. Thermal modeling of tape laying with continuous carbon fiber reinforced thermoplastic[J]. Composites, 1988, 19(5): 367-375.
[12] TUMKOR S, TURKMEN N, CHASSAPIS C, et al. Modeling of heat transfer in thermoplastic composite tape lay-up manufacturing[J]. Heat Mass Transfer, 2001, 28(1): 49-58.
[13] NOHA H, JOSEPH E T, BATRA R C, et al. A heat transfer analysis of the fiber placement composite manufacturing process[J]. Journal of Reinforced Plastics and Composites, 2005, 24(8): 869-887.
[14] LI Z M, YANG T, DU Y. Dynamic finite element simulation and transient temperature field analysis in thermoplastic composite tape lay-up process[J]. Journal of Thermoplastic Composite Materials, 2015, 28(4): 558-573.
[15] 李志猛, 杨涛, 杜宇, 等. 热塑性预浸丝铺放过程中温度场数学模型及其仿真[J]. 宇航材料工艺, 2012, 42(3): 20-23.
LI Z M, YANG T, DU Y, et al. Modeling and simulation of heat transfer in thermoplastic composite tow-placement process[J]. Aerospace Materials & Technology, 2012, 42(3):20-23.
[16] 李玥华. 热塑性预浸丝变角度铺放及其轨迹规划的研究[D]. 哈尔滨:哈尔滨工业大学, 2013.
LI Y H. Research on thermoplastic towpreg variable angle placement and trajectory planning[D]. Harbin: Harbin Institute of Technology, 2013.
[17] YARDIMCI M A, PISTOR C M, SELCUK I. Process planning for on-line consolidation in tape winding of noncircular thermoplastic composites[J]. Journal of Manufacturing Processes, 2000, 2(2): 88-99.
[18] ABHIJIT P D, JAMES C S. Crystallizability in a model high-performance thermoplastic polyimide-matrix composite[J]. Journal of Thermoplastic Composite Materials, 1999, 12(6): 498-514.

