基于过采样SVM的不平衡数据信用评价模型
朱安安

摘 要:针对信用评价中最为常见的不平衡小样本数据集问题,以及不同误分类造成的损失代价不同问题,在传统SVM模型基础上,提出采用过采样的SMOTE算法解决数据不平衡问题。在核SVM模型的基础上运用交叉验证得出核最优参数,加入非对称误差成本(DEC),提高将高风险误分为低风险的成本,建立更适用于信用评价的模型。经数据验证,该算法有效弥补了传统SVM模型在不平衡数据集分类中的缺陷,避免了小样本数据集样本过少而使得模型泛化能力降低的问题。加入DEC之后的模型与未加入的相比,虽分类准确率略有降低,但将高风险误分为低风险的错误明显降低,更适用于信用评价模型。
关键词:信用评价;不平衡数据;SMOTE算法;支持向量机;径向基核;非对称误差成本
DOIDOI:10.11907/rjdk.181205
中图分类号:TP301
文献标识码:A 文章编号:1672-7800(2018)010-0064-04
英文摘要Abstract:Aiming at the commonest problem of unbalanced data set of credit scoring and the different cost caused by different classification error,based on the traditional kernel SVM model,we propose to use SMOTE to balance the unbalanced data.Cross-validation is used to get the optimal parameters,and then dissymmetric error cost (DEC) is used to establish a more suitable model for credit scoring.Through the data test,it is proved that the new model remedies the defect of traditional SVM model and avoids the generalization ability decreasing caused by the small sample data set.Compared with the model without DEC,the accuracy of classification is slightly lower,but the error of high risk classification error is lower than before.It is more suitable for the credit scoring model.
英文关键词Key Words:credit scoring; unbalanced data; SMOTE; SVM; radial basis function kernel; dissymmetric error cost
0 引言
所谓信用评价,通常指以一系列相关指标作为考量基础,通过一定方法计算出个人或企业偿付其债务能力和意愿的过程。自美国次贷危機发生以来,各大金融机构对个人信贷业务更为谨慎。为在控制风险与追求利润之间找到平衡,建立有效的个人信用评价(credit scoring)体系更为重要[1]。在西方发达国家,个人信用评价体系、技术已逐步完善成熟,而我国信用评价起步较晚,大多数商业银行和征信机构仍然采用传统的人工经验结合打分制评判是否放贷,随着个人信用业务的迅猛增加,传统方法已无法满足现实需求。因此,如何快速有效进行信用测评显得尤为关键。在数学与计算机技术迅猛发展的今天,机器学习广泛应用于信用评价中。支持向量机由于分类效果较好,在信用评价中应用十分广泛。个人信用评价一般由专业机构针对个人相关信息,如年龄、工作状况、住房情况、其它贷款情况等进行综合分析和测定,对个人信贷风险进行预测,可以说是一种建立在定量基础上的定性判定。
由于个人信贷信息的特性,银行、信贷机构收集到的往往都是允许放贷的信息数据,因此得到的征信信息存在严重的正负样本不平衡问题。正常情况下,信贷机构拥有的信用不佳客户占比约为10%左右,而面对不平衡数据,支持向量机也只能得到次优结果,通过SVM得到的超平面偏向少数类样本,导致分类结果较差。就目前而言,抽样技术和代价敏感学习是处理数据不平衡问题的两大主流方法。抽样技术广泛应用在数据层面,为其提供一个均衡的分布,其中过采样和欠采样是最有代表性的采样方法。过采样技术通常是增加少数类样本数目,以平衡两个类别之间的比率。最简单的过采样方法就是直接复制少数类样本[2]。采用这种方法的优点是不会丢失任何信息,但可能会出现过度拟合现象。因此,出现了一些更为先进的过采样算法,例如合成少数类过采样技术(SMOTE)。
对于信用评价而言,不同类型风险错误分类的成本并不相同,具体就银行而言,把一位高风险客户错误分类为低风险的成本要比相反情况高出5倍之多[3]。因此,在原有支持向量机模型基础上,应当考虑非对称误差成本,以此作出更为合理的信用评价。
本文利用SMOTE技术选取某机构个人信用信息,将不平衡数据样本通过过采样技术变为较为平衡的数据样本,再运用含有非对称误差成本的核SVM建立模型,将数据集进行交叉验证,分析最佳模型参数,得到效果较好的信用评价模型。
1 数据不平衡问题
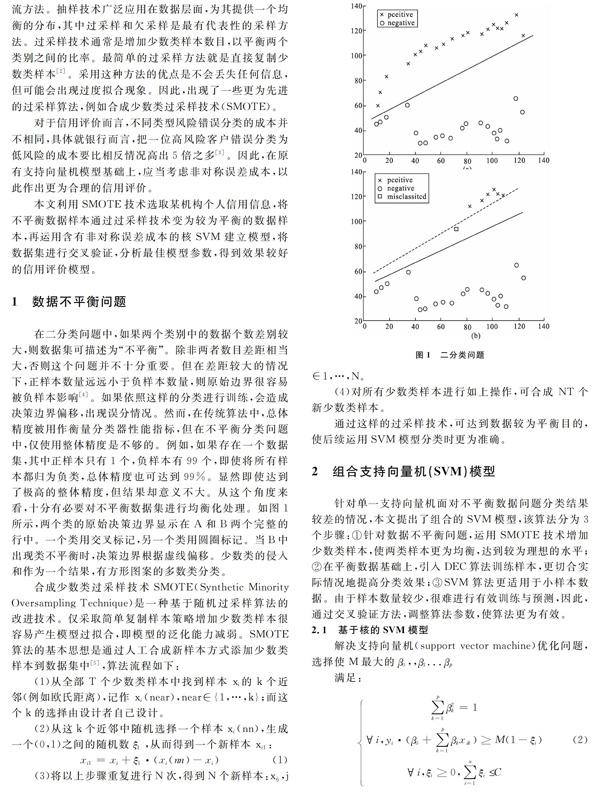
在二分类问题中,如果两个类别中的数据个数差别较大,则数据集可描述为“不平衡”。除非两者数目差距相当大,否则这个问题并不十分重要。但在差距较大的情况下,正样本数量远远小于负样本数量,则原始边界很容易被负样本影响[4]。如果依照这样的分类进行训练,会造成决策边界偏移,出现误分情况。然而,在传统算法中,总体精度被用作衡量分类器性能指标,但在不平衡分类问题中,仅使用整体精度是不够的。例如,如果存在一个数据集,其中正样本只有1个,负样本有99个,即使将所有样本都归为负类,总体精度也可达到99%。显然即使达到了极高的整体精度,但结果却意义不大。从这个角度来看,十分有必要对不平衡数据集进行均衡化处理。如图1所示,两个类的原始决策边界显示在A和B两个完整的行中。一个类用交叉标记,另一个类用圆圈标记。当B中出现类不平衡时,决策边界根据虚线偏移。少数类的侵入和作为一个结果,有方形图案的多数类分类。
在径向基核中有两个参数需要确定:①惩罚系数cost。其作用是平衡支持向量的复杂度和误分类率这两者之间的关系,可以理解为正则化系数。若cost较大,则意味着损失函数也大,会存在较多较远的离群点,这会产生更多的支持向量,使模型复杂度提高,也容易过拟合。反之,当cost较小时,表示放弃了较远的离群点,选择少量样本支持向量,最后得到的模型也会简单;②径向核的系数γ。γ的定义是单个样本对整个分类超平面的影响。当γ较小时,单个样本对整个分类超平面影响较大,也很容易被选择为支持向量。反之,当γ较大时,单个样本对超平面的影响较小,不容易被选择为支持向量。
2.2 引入非对称误差成本DEC的SVM模型
对于信用评价而言,每个类别错误分类的代价不同,如果将两种不同类型错误的成本设定成一样,则不符合信用数据集。因此,在核SVM基础上,引入非对称误差成本(DEC)[7]。在模型中提高将高风险客户误分为低风险客户的成本,虽然可能增加将低风险客户误分为高风险的误差,使分类精确度下降,但这更符合信用评价的实际情况。
2.3 交叉验证
现实环境中常遇到一种情况,即没有可用的测试数据衡量模型在未知数据集上的泛化能力,且很多数据集所含样本较少。希望将更多的数据运用在训练模型中,但也需要保留一部分样本作为验证集来验证模型分类能力,并对参数进行调整。因此,对于小样本数据集而言,交叉验证尤为有效,交叉验证概念如图2所示。
本文所用数据集存在数据量较少问题,运用最常见的k折交叉验证,即将数据集随机拆分为k个同样大小且不重叠的分区,将其中的k-1个分区用于训练模型,剩下一个分区用于测试,一共进行k次,这样可以通过对k个不同测试集获得汇总结果,调整出更适合的模型参数。如何选取k很重要,选取一个较小的k值会产生训练集样本过少,可能将更多的偏误引入模型;而使用较大的k值,模型偏误虽会降低,但实际上每次训练集数据都几乎相同,模型的泛化能力下降。参考相关文献,经验法则把k值选择为10。
3 实验与分析
3.1 数据集
本文使用某机构信用数据集,该数据集包含申请者的信用历史、贷款记录、担保人、家庭信息、就业情况、其它贷款情况等20个特征值,目标为判定申请者是否有较高的信用风险。0为信用风险良好,1表示不佳,具体如表1所示。
3.2 不平衡数据处理
本文SMOTE中,k值设置成4。当获得一个平衡的数据集后SMOTE过程会停止,在R语言下编程SMOTE,perc.over=a表示少数类样本变为原来的(1+a%)倍,perc.under=b表示多数类样本变为少数类样本的(b%*a%)。Zavgren(1985)[8]关注了信用评价中的数据不平衡问题,指出当正负样本比例为 2∶1时,分类效果更好[1],因此在该模型中a设定为200,b设定为100,将3.1节中的数据集进行均衡处理,结果如表2所示。
结果显示,在运用SMOTE均衡数据之后,正负样本比接近2∶1,趋于平衡,适用于信用评价模型。
3.3 组合SVM模型验证
为测试组合SVM模型对该数据集的有效性,采用不含有交叉验证(C-V)以及DEC的模型训练数据,再逐步引入C-V(SVM+C-V模型)和DEC(SVM+C-V+DEC模型),比较模型差异。有报告显示,将一位高风险客户误分为低风险的成本比将低风险误分为高风险的成本高5倍之多,因此在引入DEC时,本模型设定高风险误分为低风险的成本为低风险误分为高风险的5倍。
3.4 实验结果对比分析
为测试本文算法对该数据集的有效性,运用不含交叉检验与DEC的支持向量机模型对已平衡化后的数据进行测试。由于支持向量机选取径向核,因此需要选择不同的cost与γ值寻找合适的优化模型。对于平衡后的数据集,运用不同的cost值与γ值训练模型,为方便呈现,γ值只罗列每个cost值下最优结果情况,所得训练集与测试集分类精度如表3所示。
表3结果表明,当cost选取10,γ选取0.01时分类效果最好,但这种选择参数的方法一方面要消耗大量的时间,较为麻烦,另一方面,在使用了测试集指导选择参数后,它已经不再代表未知数据集,这对模型的泛化能力产生了很大的影响,为此加入交叉验证(c-v)选取参数。
运用10折交叉检验,将cost值设定在(0.01,0.1,0.5,1,5,10,100),γ值设定在(0.01,0.02,0.05,0.1,0.5,1)中,在不加入DEC的情况下,让模型自行选取最优的cost值与γ值并给出分类结果,再将非对称误差成本DEC加入模型,比较DEC对分类结果的影响。两个模型得出的最优参数结果一致,如表4所示。
由表4可以看出,运用交叉验证所得出的最优模型参数与上述不使用的一致,cost的值取10,γ值取0.01。另外,加入了DEC的模型分类准确率都比之前有所下降。但是,加入DEC之后的模型将低风险客户误分为高风险的误差增加很多,但高风险误分为低风险却有所下降,如表5所示。由于不同错误分类的成本差异很大,虽然加入DEC后模型准确率下降,但却更符合该数据集的实际情况。对于信用评价实际而言,更能幫助信贷机构降低风险,减少损失。
4 结语
针对SVM模型在不平衡数据的信用评价问题中存在的不足,提出在传统核支持向量机模型基础上,运用SMOTE过采样算法将数据正负样本比平衡至适用于信用评价的2∶1,并根据SVM适用于小样本数据情况,对模型逐步加入交叉验证、DEC,通过比较各模型之间的差异验证模型的可用性。从分类数据可以看出,交叉验证方法可以方便直观地找到本文所用径向基核的最优参数,且不会存在数据样本过少而使模型泛化能力降低的情况。将加入DEC之后的模型与未加入的比较,通过实验可以看出,虽分类准确率略有降低,但高风险误分为低风险的误差明显降低,在实际信用评价中更为可取,可为信贷机构降低此类风险提供数据支持。
参考文献:
[1] 向晖,杨胜刚.个人信用评分关键技术研究的新进展[J].财经理论与实践,2011,32(172):20-24.
[2] 黄海松,魏建安,康佩栋.基于不平衡数据样本特性的新型过采样SVM分类算法[J].控制与决策,2017,1(1):1-10.
[3] 鲁伊·米格尔·福特.预测分析R语言实现[M].北京:机械工业出版社,2017.
[4] LU W,LI Z,CHU J.Adaptive ensemble undersampling boost:a novel learning framework for imbalanced data[J].The Journal of Systems and Software,2017,132(1):272-282.
[5] 王超学,张涛,马春森.面向不平衡数据集的改进型SMOTE算法[J].计算机科学与探索,2014,8(6):727-734.
[6] 肖智,王明恺,谢林林.基于支持向量机的大学生助学贷款个人信用评价[J].清华大学学报 :自然科学版,2006,46(S1):1120-1124.
[7] ZAVGREN C V.Assessing the vulnerability to failure of American industrial firms:a logistic analysis[J].Journal of Business Finance&Accounting; ,1985,12(1):19-45.
[8] 吴敏,张化朋,李雷.欠抽样和DEC相结合的不平衡数据分类算法 [J].计算机技术与发展,2014,24(4):110-113.
[9] 梁武,苏燕.一种新的基于类内不平衡数据学习支持向量机算法[J].科技通报,2017,33(9):109-112.
[10] PALEOLOGO G,ELISSEEFF A,ANTONINI G.Subagging for credit scoring models[J].European Journal of Operational Research,2010,201(2):490-499.
[11] FINLAY S.Multiple classifier architectures and their application to credit risk assessment[J].European Journal of Operational Research,2011,210(2):368-378.
[12] 袁兴梅,杨明,杨杨.一种面向不平衡数据的结构化 SVM 集成分类器[J].模式识别与人工智能,2013,26(3):315-320.
[13] 刘东启,陈志坚,徐银,等.面向不平衡数据分类的复合SVM算法研究[J].计算机应用研究,2018,35(4):1-7.
[14] BATUWITA R,PALADE V.Class imbalance learning methods for support vector machines[J].Imbalanced learning:Foundations,algorithms,and applications,2013(6):83-99.
[15] 王伟,薛安荣,刘峰.改進的SVM解决背景知识数据中的类不平衡[J].计算机应用研究,2011,28(8):2902-2904.
[16] 楼晓俊,孙雨轩,刘海涛.聚类边界过采样不平衡数据分类方法 [J].浙江大学学报:工学版,2013,47(6):944-950.
[17] 李勇,刘战东,张海军.不平衡数据的集成分类算法综述[J].计算机应用研究,2014,31(5):1287-1291.
(责任编辑:杜能钢)

