再论非平衡桥式电路等效电阻的求法

田社平， 张 峰

(上海交通大学 电子信息与电气工程学院, 上海 200240)

0 引言

桥式电路既是工程实际中常用的电路，也是电路理论/电路分析教学中常出现的电路。在当前实际教学中，对桥式电路一般多通过T-Π形电路的等效变换化简的方法来分析[1-3]。文献[4]在此基础上给出多种求解非平衡电桥电路等效电阻的求解方法。本文基于笔者的教学实践，通过建立一端口电路和二端口电路之间的关系，给出了一种新的分析非平衡电桥电路等效电阻的方法，供大家参考。本文的讨论可看作对文献[4]的补充。

1 基于二端口VCR的分析

为便于比较，本文仍以如图1所示的非平衡桥式电路为例加以讨论[4]。

对非平衡桥式电路，由于对角支路cd的存在，使得从输入端口ab看进去的电路拓扑不是由电阻串、并联构成的简单混联连接方式，从而无法利用电阻串、并联的等效变换进行化简。因此，可考虑断开对角支路cd，使电路构成一个二端口电路，如图2(a)所示。该二端口电路的VCR用g参数矩阵可表示为

图1 非平衡桥式电路

(1)

(a) 二端口电路

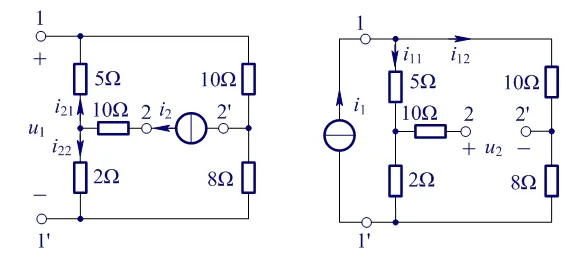
(b) 求r12的电路 (c) 求r21的电路图2 非平衡桥式电路等效电阻的求解之一

由g参数的定义可知，g11为端口11′的短路策动点电导，它也就是图1电路的端口等效电导。因此求出参数g11也就得到了图1电路的端口等效电阻，即Rab=1/g11。

显然，直接按照定义求解参数g11是比较复杂的。为此，可将图2(a)所示二端口电路的VCR用r参数矩阵表示为

(2)

如果能够求出r参数，则利用r参数矩阵与g参数矩阵的关系即可求出g参数。观察图2(a)，不难发现可简便地求出r参数。

由图2(a)，可得

(3)

为求r12，如图2(b)所示，由分流公式可得

(4)

由KVL可得

(5)

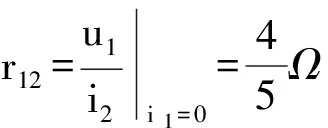
为求r21，如图2(c)所示，由分流公式可得

(6)

由KVL可得

(7)

由上面的分析可知r12=r21，这也说明二端口电路是互易的。得到r参数后，即可求得

(8)

因此Rab=1/g11=5 Ω

2 构成二端口电路的形式

在上面分析中，我们通过断开对角支路cd来构成二端口电路。是否存在构成二端口电路的其他形式呢？事实上，通过断开图1中任意支路来构成二端口电路均可较方便地使问题得到求解。下面仅以如图3(a)所示的断开10 Ω桥臂支路为例加以说明。

(a) 二端口电路 (b) 求r12的电路图3 非平衡桥式电路等效电阻的求解之二

由图3(a)，可得:(田社平等文)

(9)

为求r12，如图3(b)所示，由KVL可得

(10)

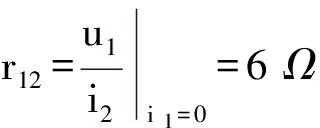
而由互易性，得到r21=r12=6 Ω

由r参数即可求得

(11)

因此Rab=1/g11=5 Ω

3 结语

从电路结构看，非平衡电桥电路不能直接利用电阻串、并联等效进行化简，其常见的处理方法是利用T-Π形电路的等效变换将电路简化为可以利用电阻串、并联等效的电路形式。

本文讨论的是利用二端口参数矩阵来求解非平衡电桥电路等效电阻，该方法充分利用了二端口g参数与一端口等效电阻间的关系以及二端口参数矩阵之间的关系，从而简化了求解的过程。尽管这种方法需要理解二端口参数的含义，但避免了对T-Π形电路的等效变换公式的识记。该方法拓展了分析思路，将一端口和二端口电路的知识点进行了联系，将其应用于电路教学，可加深学生对该电路以及相关电路知识点的理解。本文的讨论可供从事电路教学的教师参考。

[1] 田社平. 电路理论基础[M]. 上海：上海交通大学出版社，2016.

[2] 于歆杰，朱桂萍，陆文娟. 电路原理[M]. 北京：清华大学出版社，2007.

[3] 陈洪亮，田社平，吴雪. 电路分析基础教学指导书[M]. 北京：清华大学出版社，2010.

[4] 田社平，张峰. 关于非平衡桥式电路等效电阻求法的讨论[J]. 南京：电气电子教学学报，2016，Vol.38(4)：86-88.