线性卷积与循环卷积等价关系及水声通信应用
戚晨皓, 王 昕, 张在琛
(东南大学 信息科学与工程学院, 江苏 南京 210096)
0 引言
在“数字信号处理”课程教学中,卷积运算占据重要地位。其中,线性卷积与循环卷积之间的关系是学习过程中的难点之一。循环卷积和周期卷积的过程是一致的,不同的是循环卷积仅取周期卷积的主值序列。而周期卷积又是线性卷积的周期延拓,因此,可通过周期卷积在循环卷积和线性卷积之间建立联系[1,2]。
在计算周期卷积时,需要对两个有限长序列的线性卷积的结果按照卷积周期进行延拓,当周期长度小于线性卷积结果的长度时,会发生混叠现象[3]。在计算循环卷积时,通常利用线性卷积的周期延拓先计算周期卷积,再对周期卷积取主值区间得到循环卷积;该过程等价于将线性卷积结果的尾部加到头部并将尾部删除,其中相加的位数等于发生混叠的位数,这样可直接得到循环卷积的结果。
通常,“数字信号处理”课程只介绍线性卷积与循环卷积的等价关系,没有介绍其具体应用。由于线性卷积与循环卷积的等价关系具有一定难度,为了激发学生的兴趣、加深学生对这一关系的认识,结合具体应用加以讲授,这不失为一种可行的教改探索。
本文介绍了线性卷积与循环卷积的等价关系在水声通信这一海洋信号处理领域的研究热点中的应用。由于水声信道时延很大,采用循环前缀填充保护间隔的正交频分复用OFDM(Orthogonal Frequency Division Multiplexing)技术会占用很大的发射功率,因此,在水声通信中常用补零ZP(Zero Padding)填充OFDM的保护间隔;相应的,在接收端需采用首尾混叠相加法消除符号间干扰ISI(Inter-symbol Interference)。
本文首先简单回顾了“数字信号处理”课程中循环卷积、周期卷积与线性卷积之间的等价关系,随后介绍了水声通信中的ZP-OFDM系统。为消除ISI,给出了保护间隔长度所需满足的条件以及在保护间隔内补零后接收端实施首尾混叠相加法的步骤。最后通过Matlab实例,演示了首尾混叠相加法消除ISI的过程。
1 循环与线性卷积之间的等价关系
有限长序列x(n)与y(n)的长度分别为N1、N2,取L≤max{N1,N2},将x(n)与y(n)分别补零到L长度,记作xL(n)和yL(n),再以L为周期构造两个周期序列为
(1)
(2)
则周期卷积为
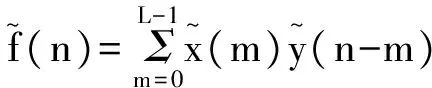
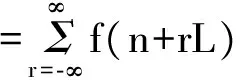
(3)
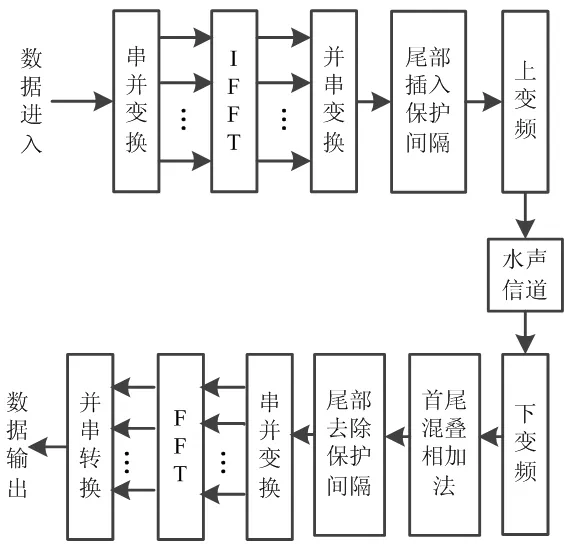
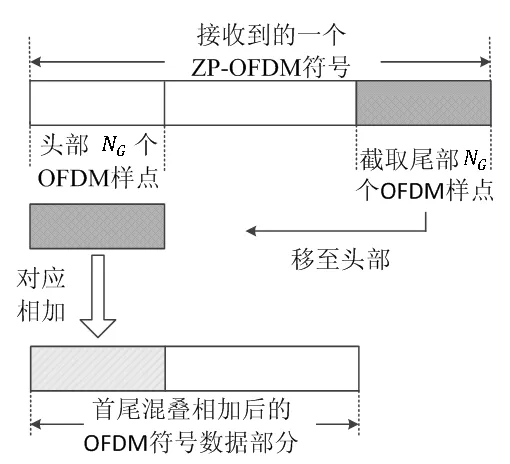
式中,f(n)就是xL(n)和yL(n)的线性卷积,长度为N1+N2-1。可以看到,当卷积周期L 需要注意的是,本文的首尾混叠相加法与“数字信号处理”课程介绍的重叠相加法不同,重叠相加法涉及到两个不同的分段之间的线性卷积输出的重叠相加,而本文的首尾混叠相加法仅仅是在同一个分段内部将尾部重叠相加到头部,并且把尾部删除。 水声信道中,发送信号经过水面、水底的多次反射和散射到达接收端,密集的多径效应造成严重的频率选择性衰落,导致信道具有很强的频率选择性[5]。另一方面,水声信道时变性强,不同水域、不同温度、不同盐度都会导致水声信道传输特性不同,远不如无线信道稳定。水声信道具有频率和时间双重选择性,给高速可靠的水声通信带来巨大挑战。 由于声信号在水中的传播速度远小于无线电波在空气中的传播速度,水声通信收发机较小的相对运动即会产生显著的多普勒频偏。 现有的单载波水声通信系统通常在接收端使用自适应判决反馈均衡器消除水声信道引起的ISI,由于水声信道时延扩展很大,均衡器长度很长,有时甚至高达上百上千个抽头,复杂度很高。而OFDM多载波传输系统,可将频率选择性信道有效转换成若干并行的频率平坦子信道,大大降低了接收端均衡器的复杂度,因此,将OFDM技术应用到水声通信中是目前水声领域的研究热点之一。 考虑到水声信道时延扩展很大,而OFDM保护间隔长度要不小于信道时延扩展,采用循环前缀填充保护间隔的OFDM系统在循环前缀部分会占用很大的发射功率,因此,在水声通信中常用补零填充OFDM的保护间隔,形成ZP-OFDM系统。该系统框图如图1所示,发送端主要包括串并变换、IFFT、并串变换、尾部插入保护间隔、上变频等部分;接收端主要包括下变频、首尾混叠相加法、尾部去除保护间隔、串并转换、FFT、并串转换等部分。 图1 ZP-OFDM系统框图 在OFDM系统中,为消除ISI,通常需要在每个OFDM符号间插入一定长度的保护间隔。假设每个OFDM符号由Nu个数据部分和NG个保护间隔部分组成,满足 NG≥L-1 (4) 由于声信号在海水中的传播速度约为1500米/秒,远小于无线电波在空气的传播速度3×108米/秒,在相同传输距离下,水声信道中的时延要比无线信道中的时延大得多。如果采用传统的循环前缀填充保护间隔的方法,会占用很大的发射功率,所以在水声通信中,保护间隔通常使用零填充,即ZP-OFDM。此外,填充零元素具有更强的鲁棒性。 OFDM发送端首先通过串并转换将输入连续的数据流转换为若干个并行的长度为Nu的数据向量;其次,每个数据向量通过IFFT得到每个OFDM符号的数据部分,通过并串转换以后得到su,在su尾部增加长度为NG(NG≥L-1)的全零序列szp,之后将完整的OFDM符号s=[su,szp]发送进入冲激响应为h为水声信道,信道长度为L。发送信号与接收信号之间的关系表示为 r=s*h+n (5) 其中,n是加性噪声向量。 接收端采用首尾混叠相加进行OFDM信号解调。首尾混叠相加的本质是用线性卷积来计算循环卷积。 首尾混叠相加法的具体步骤如下: 首先保留接收信号r的前Nu个OFDM样点,其次将尾部的NG个OFDM样点对应加到头部的NG个OFDM样点上,最终得到所需的ru,即 ru= [r(0)+r(Nu),r(1)+r(Nu+1)], …,r(NG-1)+r(Nu+NG-1), r(NG),r(NG+1),…,r(Nu-1)] (6) 该过程如图2所示。得到所需的ru后,再依次进行串并转换、FFT、并串转换以后,提取出发送数据。不难发现,ru是su与h的Nu点循环卷积与信道加性噪声之和,即 ru=suh+η (7) 图2 首尾混叠相加法示意图 其中,η为长庋Nu的加性噪声。进而具有如下关系 DFT{ru}=DFT{su}·DFT{h}+DFT{η} (8) (9) 假设水声信道冲激响应序列为h,即水声信道长度L=3;设OFDM符号的数据部分su=[1,2,3,4,5,6],长度Nu=6。根据式(4)可计算得到ZP的长度NG≥2。本例不妨取NG=2,尾部补零以后构成完整的ZP-OFDM符号s=[1,2,3,4,5,6,0,0]。发送信号通过水声信道的过程可使用Matlab库函数filter实现;信道噪声可通过库函数awgn实现。由于本例重点关注首尾混叠相加法,此处忽略信道噪声。因此,r=filter{h,1,s}={3,8,14,20,26,32,17,6} filter函数本质上实现了线性卷积,在su尾部补2个零的作用是使filter输出等价于su与h的线性卷积输出。根据式(6)得到ru=[20,14,14,20,26,32]。其实,ru为发送的OFDM符号数据部分su与h的Nu点循环卷积,即ru=IDFT{DFT{su}DFT{h}},计算可得ru[20,14,20,26,32]。 当ZP长度不满足式(4)时,例如NG=1时,s=[1,2,3,4,5,6,0],r=[3,8,14,20,26,32,17],ru=[20,8,14,20,26,32]。但是su和h的Nu点循环卷积的结果[20,8,14,20,26,32]和ru不同,说明发生了ISI。由此也验证了式(4)。 “数字信号处理”课程通常只介绍线性卷积与循环卷积的等价关系的理论部分,并未涉及它的实际应用,由于比较抽象,学生掌握时具有一定难度。本文通过结合水声通信中的ZP-OFDM系统介绍线性卷积与循环卷积的等价关系,理论联合实际,不但可以进一步加深学生对两种卷积关系等基础知识与重要概念的理解,还可以拓展学生的专业知识面,在实际教学中已获得较好反响。 [1] 吴镇扬. 数字信号处理[M]. 第3版,北京:高等教育出版社,2016. [2] 王大伦.数字信号处理[M]. 第1版,北京:清华大学出版社,2014. [3] 胡广书.数字信号处理导论[M]. 第2版,北京:清华大学出版社,2013. [4] 程佩青. 数字信号处理教程[M]. 第4版,北京:清华大学出版社,2013. [5] C. Qi, L. Wu and X. Wang. Underwater Acoustic Channel Estimation via Complex Homotopy [C], in Proc. IEEE International Conference on Communications (ICC), pp. 3821-3825, Ottawa, June 2012.2 水声通信中的ZP-OFDM系统
3 首尾混叠相加法在ZP-OFDM中的应用
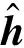
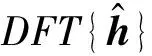
4 Matlab实例
5 结语

