绝缘子检测机器人振动阻尼比计算新方法研究

胡 雯，赵 淳

（1.湖北经济学院信息工程学院，湖北 武汉 430205；2.国网电力科学研究院武汉南瑞有限责任公司，湖北 武汉 430074）

1 引言

架空输电线路绝缘子长期暴露于复杂、恶劣的野外环境中，极易遭受工业废气、沙尘、自然盐碱、酸雨等污染物的侵蚀，绝缘性能不断降低，甚至不定期地出现劣化或零值现象。绝缘子带电检测机器人能够安全、快速地采集绝缘子的分布电压，通过对分布电压数据分析，进而判断其劣化情况。绝缘子带电检测机器人在进行作业时，需要保持其机体姿态的稳定。因此，对绝缘子检测机器人振动状态进行监测、控制尤为重要，关系着绝缘子检测机器人作业的安全性、可靠性和准确性。振动是一种机械工程中经常发生的现象，阻尼是耗散振动能量的一种物理作用。在结构损伤检测、安全评估、振动控制等研究领域中，阻尼比是一个非常重要的特征参数。阻尼比的估计方法主要有：对数衰减率法[1-2]、信号能量分析法[3]、分段FFT变换法[4-5]等。对数衰减率法在计算振动阻尼比过程中容易受到噪声的干扰，计算结果的精度相对较低，无法满足工程及基础研究的需要。信号能量分析法和分段FFT变换法都要对振动信号进行分段，会由于分段条件的选取而造成估计结果精度不高。基于信号质心的绝缘子带电检测机器人振动阻尼比计算方法是对数衰减率法的一种优化方法。虽然噪声会影响振动采样信号的局部信息，但是不会对信号质心位置造成影响。因此，提出的阻尼比计算方法具有物理概念清晰、计算精度高等特点。

2 架空线路绝缘子带电检测机器人振动影响分析

架空输电线路绝缘子带电检测机器人的三维结构模型，如图1所示。绝缘子检测机器人由机器人本体和检测模块组成，机器人本体包括上层机架、下层机架、爬行机构、导向机构。上层机架和下层机架通过导向机构连接在一起，爬行机构附着在上层机架和下层机架之间。绝缘子检测机器人在爬行过程中依靠爬行机构的手爪卡住绝缘子完成行走动作；其搭载的检测模块采集绝缘子分布电压时，检测模块探针需要与钢脚、钢帽连接处充分接触。由于工作环境影响和机器人关节动作，绝缘子检测机器人会发生振动现象。这种振动直接影响手爪与绝缘子的可靠接触，导致手爪无法卡住绝缘子，甚至会出现手爪损坏绝缘子釉面的问题。此外，这种振动影响探针与绝缘子钢脚、钢帽的可靠接触，导致分布电压采集值不准确。机体的振动现象也会使机器人的结构件连接部位松动。所以，深入分析机器人的振动特性为改善机器人动作及性能的准确性和安全性提供保障[6]。

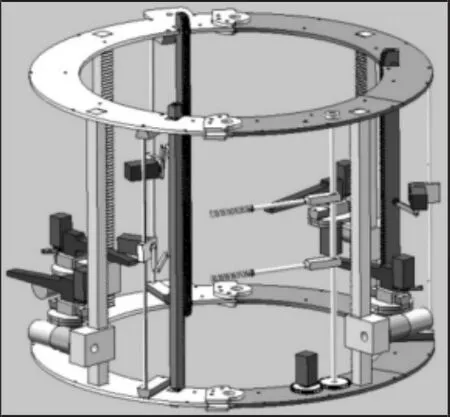
图1 机器人结构模型Fig.1 The Structure Model of the Robot

3 基于信号质心算法的振动阻尼比计算方法分析

3.1 传统对数衰减率法原理分析

基于动力学理论可知衰减振动微分方程为[7]：

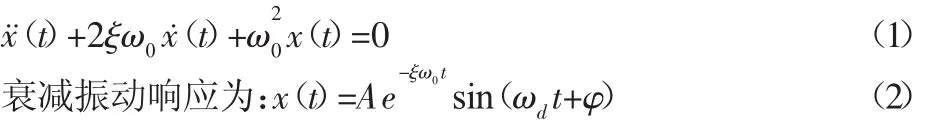
式中：ξ—系统的阻尼比；ω0—固有角频率；ωd=ω0—振动角频率；A，φ—由初始条件确定的常数，且：

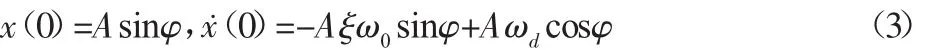
传统的对数衰减率法为[8]：

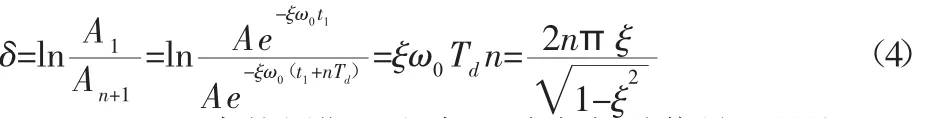
式中：T=2π/ω—自然周期。由式（4）求得振动信号阻尼比ξ。

问题分析：对数衰减率法中的峰值A1、An是振动响应的采样值，容易受到外界噪声影响；如果x（n）受到外界噪声影响，A1、An在局部会产生剧烈震荡，偏离实际值，从而降低振动阻尼比ξ的计算精度。

3.2 基于信号质心的振动阻尼比计算方法研究

质量中心（centre of mass）简称质心，指物质系统上被想象为质量集中于此的一个假定点，该假定点对于坐标轴的矩等于该系各点的质量对同一坐标轴的矩之和[9]。信号质心的坐标系公式为：

式中：X—信号质量中心；mi—信号某i点的质量；xi—信号某i点坐标。

由于采样得到的振动信号x（t）会出现小于零的值，所以优化信号质心公式为：

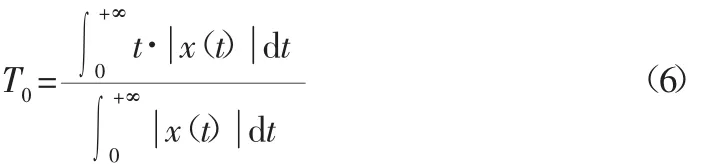
在实际的架空输电线路绝缘子检测机器人振动信号中x（0）=0，则φ=0。对式（6）化简得：

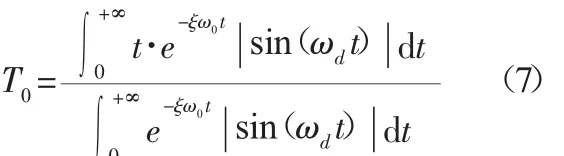
由式（7）可知绝缘子检测机器人振动信号质心T0、振动的角频率ωd、阻尼比与固有角频率乘积的函数关系ξ·ω0，如图1所示。由图2可知：绝缘子检测机器人振动角频率改变时，振动信号质心位置坐标基本不会发生变化；而ξ·ω0改变时，振动信号质心的坐标数值也会随之有规律的改变。所以，绝缘子检测机器人振动信号质心位置坐标与阻尼比和固有角频率乘积ξ·ω0存在一定的关联。

推测在绝缘子检测机器人振动中，阻尼比和固有角频率乘积ξ·ω0与信号质心T0的乘积的关联是关于ξ·ω0的函数，即：

为进一步验证推测，对ξ·ω0·T0与ξ·ω0的联系做更为深入的分析，得出的结果，如图2所示。

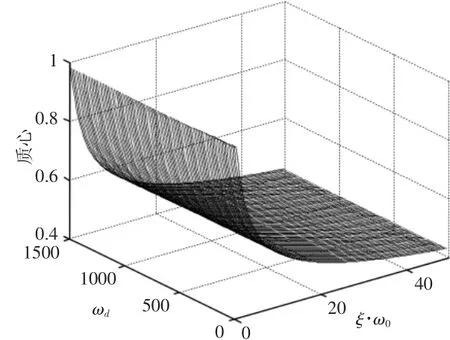
图 2 T0，ωd和 ξ·ω0的关系Fig.2 Relationship between T0，ωdand ξ·ω0

运用最小二乘法对图 3 中的 ξ·ω0·T0与 ξ·ω0关系曲线进行三次拟合，确定 ξ·ω0·T0与 ξ·ω0的函数关系。进而确定质心 T0与ξ·ω0的函数关系。结论在架空输电线路绝缘子带电检测机器人振动中，阻尼比和固有角频率乘积ξ·ω0与信号质心T0呈现非线性关系，如表1所示。

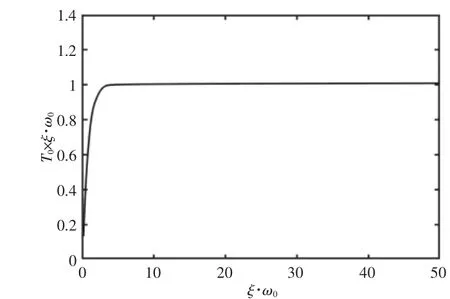
图 3 ξ·ω0·T0与 ξ·ω0的关系曲线Fig.3 Relation Curve between ξ·ω0·T0and ξ·ω0

表 1 质心 T0与 ξ·ω0的函数关系（a=ξ·ω0）Tab.1 Function of T0and ξ·ω0

在动力学理论中，对数衰减率δ与阻尼比和固有角频率乘积ξ·ω0和ωd的函数关系，如式（9）所示。阻尼比ξ与对数衰减率δ的函数关系如式（10）所示[10]。

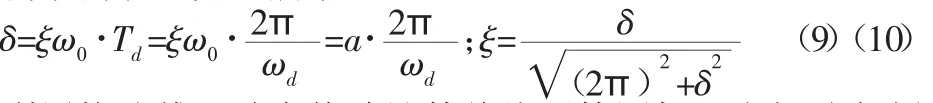
利用快速傅里叶变换法计算绝缘子检测机器人振动角频率，由式（6）计算机器人振动信号质心并基于表1中的函数表达式计算阻尼比和固有角频率乘积ξ·ω0，基于式（9）计算δ，根据式（10）计算振动信号的阻尼比ξ。

4 仿真计算与实测试验

4.1 仿真计算

假定衰减振动的微分方程为：x¨（t）+20x˙（t）+40000x（t）=0（11）

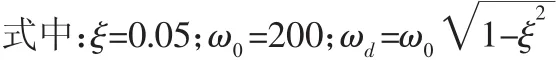
令 x（0）=0、x（0）=100，则 A=0.5006，φ=0。

振动微分方程的解为：x（t）=0.5006e-10tsin（199.75t）

图4 加入零均值高斯白噪声之后的振动波形Fig.4 The Vibration Waveform after Adding Zero Mean White Gauss Noise

取信号的采样频率fs=2397Hz，采样点数N=4794，在衰减振动信号中依次分别加入信噪比为10dB，20dB，30dB的零均值高斯白噪声，取（0～1）s的振动信号波形，如图4所示。应用MATLAB软件并利用基于信号质心的阻尼比估计算法计算这组振动信号的阻尼比，仿真结果，如表2所示。

表2 计算方法仿真结果比较Tab.2 Simulation Results Compare

4.2 实测试验

架空输电线路绝缘子检测机器人振动试验是利用朗斯LC0104振动加速度传感器采集绝缘子检测机器人在爬行过程中因工作环境变化（架空输电线路绝缘子串发生受迫振动）引起机器人机体振动的一段信号波形（采样频率2500Hz，各样本长度1.6s），如图5所示。人为不断改变架空输电线路绝缘子串受迫振动的程度，测出一组绝缘子检测机器人的振动信号波形，对这组振动信号波形进行阻尼特征分析，得到一组绝缘子机器人振动阻尼比的估计结果，如图6所示。对这组绝缘子检测机器人的振动阻尼比数据进行计算分析，这组阻尼比数据的平均值为0.005019，均方差为0.14%，计算结果稳定。

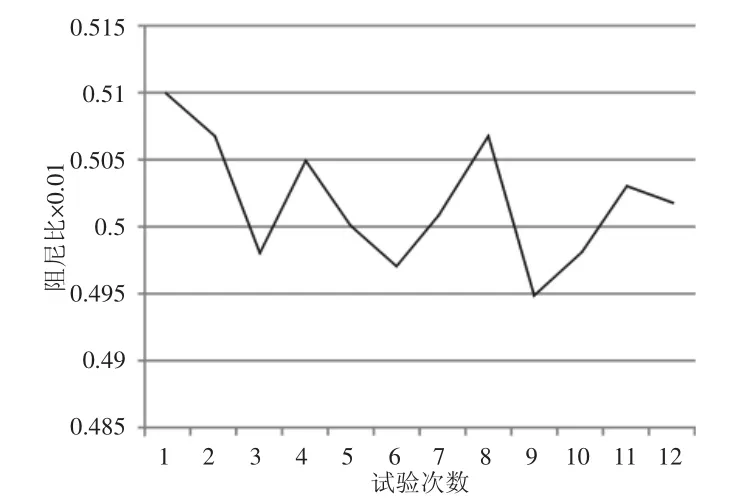
图6 阻尼比计算结果Fig.6 Calculation Results of Damping Ratio

5 结论

信号质心通过“采样值与时间乘积求和/采样值求和”的方法获得，信号质心获取方式简单、快速，容易应用于架空输电线路绝缘子检测机器人的振动状态监测中。虽然噪声会影响振动采样信号的局部信息，但是不会对信号质心位置造成影响。在有外界噪声影响的条件下，基于信号质心的阻尼比计算方法仍能具有较好的计算精度。所以，基于信号质心的阻尼比计算方法适合绝缘子检测机器人的振动特征分析。

［1］诸德超，邢誉峰.工程振动基础［M］.北京：北京航天航空大学出版社，2004.（Zhu De-chao，Xing Yu-feng.Engineering Vibration Foundation［M］.Beijing：Beijing University of Aeronautics and Astronautics Press，2004.）

［2］李中付，华宏星，宋汉文.用时域峰值法计算频率和阻尼［J］.振动与冲击，2001，20（3）：5-6，31.（Li Zhong-fu，Hua Hong-xing，Song Han-wen.The frequency and damping are calculated by using the peak value method in the time domain［J］.Journal of Vibration and Shock，2001，20（3）：5-6，31.）

［3］曾储惠，黄方林，柳成荫.基于信号能量分析的结构阻尼比识别方法［J］.振动与冲击，2003，22（2）：66-68，42.（Zeng Chu-hui，Huang Fang-lin，Liu Cheng-yin.Structural damping ratio identification method based on signal energy analysis［J］.Journal of Vibration and Shock，2003，22（2）：66-68，42.）

［4］王宗林，李伟钊，盛可鉴.基于跑车余振的混凝土桥梁阻尼比估计算法［J］.振动、测试与诊断，2012，32（3）：414-418.（Wang Zong-lin，Li Wei-zhao，Sheng Ke-jian.A damping ratio estimation algorithm for Concrete Bridges Based on the residual vibration of the sports car ［J］.Journal of Vibration，Measurement and Diagnosis，2012，32（3）：414-418.）

［5］刘爽，魏伟，何卫东.四环板针摆行星减速器振动测试与分析［J］.机械设计与制造，2014，2（2）：167-170.（Liu Shuang，Wei Wei，He Wei-dong.Test and analysis of vibration of four ring-plate cycloid gear reducer［J］.Machinery Design and Manufacture，2014，2（2）：167-170.）

［6］徐志翔，吴功平，刘席洲.架空高压输电线路走廊树枝修剪机器人研究［J］.机械设计与制造，2014，9（9）：204-207.（Xv Zhi-xiang，Wu Gong-ping，Liu Xi-zhou.Research power line corridor tree-trimming robot［J］.Machinery Design and Manufacture.2014，9（9）：204-207.）

［7］殷祥超.振动理论与测试技术［M］.徐州：中国矿业大学出版社，2007.（Yin Xiang-chao.Vibration Theory and Testing Techniques［M］.Xuzhou：China Mining University Press，2007.）

［8］L.B.Magalas，T.Malinowski.Measurement techniques of the logarithmic decrement［J］.Solid State Phenomena，2003：247-260.

［9］刘向丽，李赞，胡易俗.无线传感网中基于质心的高效坐标压缩算法［J］.物理学报，2013，62（7）：1-7.（Liu Xiang-li，Li Zan，Hu Yi-su.Acoordinate compression algorithm based on centroid for wireless sensor networks［J］.Acta Phys.Sin.2013，62（7）：1-7.）

［10］周海俊，孙利民.被动磁流变阻尼器的实索减振试验研究［J］.振动与冲击，2008，27（6）：92-95.（Zhou Hai-jun，Sun Lin-min.Experimental study on real cable vibration reduction of passive magneto rheological damper［J］.Journal of Vibration and Shock，2008，27（6）：92-95.）