基于改进蚁群算法的移动机器人路径规划研究

王志中

（重庆建筑工程职业学院，重庆 400072）

1 引言

随着机器人人工智能的不断提高，机器人能够更加自觉、高效地为人类服务。机器人作为多个学科领域的集合体，其可以为代替人类劳动[1]，将人类从反复的体力劳动中解放出来，如室内清洁机器人、机械臂；也可以完成人类无法进行或难以进行的工作，如擦窗机器人、月球车等。机器人路径规划问题是机器人导航研究的重点，是对机器人导航需要解决的首要问题[2]。因此寻求一条路径最短、收敛最快、能够避开障碍的最优路径，对解决机器人导航问题具有重要意义。按照对机器人工作环境信息的掌握程度，机器人路径规划可以分为全局路径规划和局部路径规划[3]。全局路径规划是机器人工作环境已知，当前的全局路径规划方法有栅格解耦法[4]、拓扑图法[5]、可视图[6]等。局部路径规划是指机器人工作环境未知，是一种边探测工作环境边进行路径规划的问题，局部路径规划方法有人工势场法[7]、模糊逻辑算法[7]、遗传算法[8]等。这些方法在全局或局部路径规划中都取得了很好的效果，当前使用智能算法的群智能特性寻找机器人避障的最优路径称为机器人研究的热点问题。介绍了栅格环境建模方法，将工作环境转化为机器人可以识别的数学模型，分析了蚁群算法原理，对路径搜索策略和路径选择策略提出了改进方法，并提出了信息素挥发系数的自适应调整方法，改进算法与传统算法相比，具有更快的收敛速度、更集中于最优路径、更优的最优解。

2 栅格法原理

研究的是全局路径规划问题，机器人路径规划问题可以分为两部分，一是工作环境建模，二是路径规划方法。环境建模就是将机器人工作区域转化为机器人可以识别的数学模型，在全局路径规划中最常用的环境建模方法为栅格法。栅格法就是在机器人工作环境上建立二维直角坐标系，而后按照障碍物和机器人尺寸确定栅格大小，以固定尺寸的栅格分割工作环境，此时根据栅格区域的障碍物情况，可以将栅格分为三类，一是障碍物栅格，二是可行驶区域栅格，三是半障碍物栅格，为了使机器人能够识别工作环境，将第一类和第三类栅格全部归为障碍物栅格，对此类栅格赋值为1，对可行驶栅格赋值为0，这样机器人就可以根据栅格的属性值区分障碍物和可行驶区域。所有栅格的边长定义为1。栅格的标识具有两种方法，一是使用直角坐标法（x，y），二是序号法，按照X、Y轴正方向进行编号，两种方法可以相互转换。选用相对简单的序号法对栅格进行标识，如图1所示。图中黑色部分为障碍物栅格，白色部分为可行驶栅格。

3 蚁群算法原理

3.1 旅行商问题

为了方便对蚁群算法进行分析，首先给出旅行商问题（也叫TSP问题）。旅行商问题是指给定m个城市及任意两城市之间的距离，要求找到一条经过任何城市一次、且只经过一次的最短路径。将m个城市分别表示为p1，p2，…，pm，城市pi和pi+1之间的路径长度记为d（pi，pi+1），则旅行商问题的数学模型可以描述为：

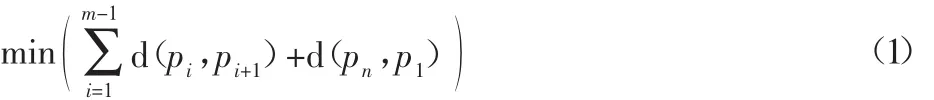
3.2 蚁群算法分析

以旅行商问题为背景，对蚁群算法进行分析。假设在初始时刻，任意两城市i、j之间的信息素相同，记为τij（0），且两城市之间距离记为dij。将n只蚂蚁随机放置在起点城市，蚂蚁k下一步要转移的城市按照随机比例规则[9]进行选择，概率公式为：

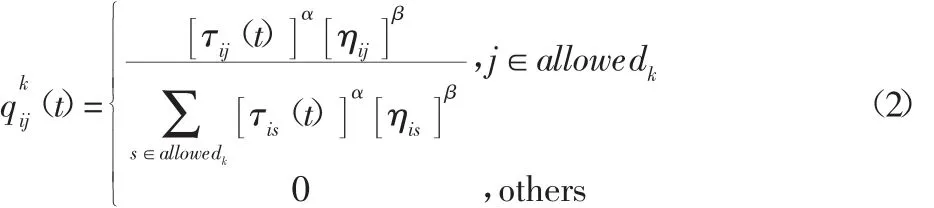
式中：τij（t）—在t时刻，从i城市到j城市路径上的信息素浓度；α—信息启发因子；ηij=1/dij—两城市之间距离对蚂蚁选择的影响；β—期望启发因子；allowedk—蚂蚁k下一步允许到达的城市集合，在此集合中包含蚂蚁k尚未到达的所有城市的集合，这种设置是为了保证所有城市均经历，且只经历一次。α值的大小代表信息素浓度对蚂蚁运动的影响大小，其值越大，表明蚂蚁越倾向于走其它蚂蚁走过的路径；β值的大小代表能见度对蚂蚁运动的影响大小，其值越大，路径的选择越接近于贪心规则[10]。

按照上述规则，当经过m个时刻后，n只蚂蚁均完成一次全城市遍历，计算每只蚂蚁的路径长度，并保存所有路径中的最短路径，然后进行信息素更新。信息素的更新包括两部分，一是各路径上信息素的挥发，二是蚂蚁在所经过路径留下的信息素。记Δτij（t）为所有蚂蚁在城市i、j路径上单位长度轨迹的信息素，则所有蚂蚁完成一次遍历后的信息素更新公式为：

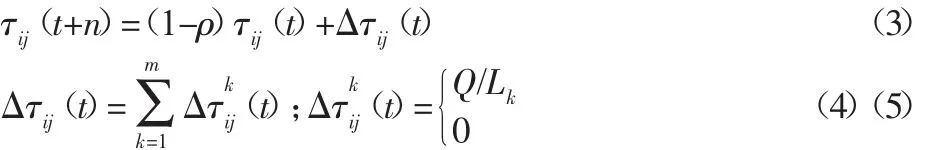
式中：ρ—信息素的挥发系数；Δτkij（t）—蚂蚁 k 在城市 i、j路径上留下的信息素浓度；Q—蚂蚁携带的信息素强度；Lk—蚂蚁k完成城市遍历的路径长度。

由式（5）可以看出，蚂蚁k在城市i、j路径上留下的信息素浓度与其路径的优化层度有关，路径越短，则留下的信息素浓度越高，否则信息素浓度就低。

4 改进的蚁群算法

4.1 路径搜索策略的改进

算法的起始时刻各路径上的信息素量均为0，信息素浓度的差异要在一段时间后才能表现出来，因此在蚁群算法起始的一段时间内，信息素对蚁群的引导作用不存在，使得算法路径搜索时间过长，为了提高可行解的搜索效率，提出了蚂蚁相遇策略、蚂蚁回退策略。蚂蚁相遇策略。在传统蚁群算法中，n只蚂蚁随机放置在起点，而后各自自由地进行路径搜索，算法搜索效率低、搜索速度慢。为了提高蚁群算法的搜索效率，将n只蚂蚁平均分成两组，记为A组和B组，指定A组从起始点到目标点进行路径搜索，B组从目标点到起始点进行路径搜索，A组蚂蚁相当于寻找食物过程，B组蚂蚁相当于将食物运回蚁巢过程。对蚂蚁k赋属性值directionk，directionk=0表示蚂蚁属于A组；directionk=1表示蚂蚁属于B组，directionk值在搜索到最优路径后进行更新。当A组和B组的蚂蚁相遇时，将两组蚂蚁的路径连线就得到了一条可行路径，尤其对于复杂工作环境，此方法可以极大地提高搜索效率。蚂蚁k1、k2的相遇定义为当满足d（p1，p2）≤ 2 时，两只蚂蚁相遇，此时的路径长度为：L=L（k1）+L（k2） （6）

式中：L（k1）、L（k2）—相遇的蚂蚁中两方向各自的最短路径。

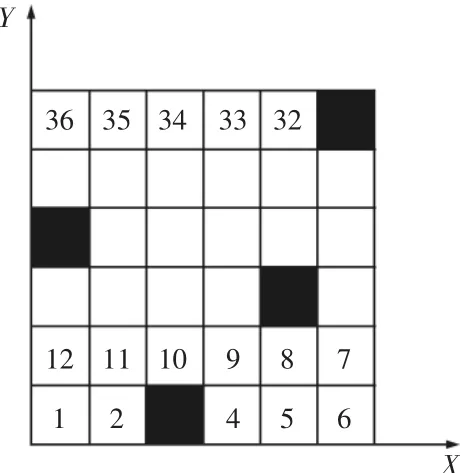
图1 栅格标识法Fig.1 Marking Method of Grid

图2 U形陷阱示意图Fig.2 U-shaped Trap

蚂蚁回退策略。记蚂蚁k在ti时刻的可行节点集合为gatheri，随着算法的进行，一些蚂蚁可能会进入U形陷阱，使自身的可行栅格集合为空集，此时蚂蚁陷入死锁，如图2所示。此类现象严重影响算法的适应度和鲁棒性。

4.2 路径选择策略的改进

蚂蚁对路径的选择与路径上信息素的浓度有很大关系，路径的选择与信息素的释放是一种正反馈机制，也就是说路径上的信息素浓度越高则此路径越容易被选择，而此路径越容易被选择则残留在此路径上的信息素也就越多。这种正反馈机制是蚁群算法群智能性的核心，但是同时从算法的开始阶段就限制了路径选择的多样性。为了使蚁群在算法的初始阶段能够对可行解空间进行大范围搜索，增加解的多样性，对蚂蚁的信息素感应设定阈值h0，当信息素浓度h＜h0时，蚂蚁感应不到信息素，此时信息素对蚂蚁的导引作用也就不存在，此时蚁群可以对可行路径进行大范围搜索；当算法进行到一定阶段，路径上信息素积累到一定程度即h≥h0时，信息素对算法的导引作用开始体现。也就是说，此时蚂蚁从i城市到j城市选择概率公式为：

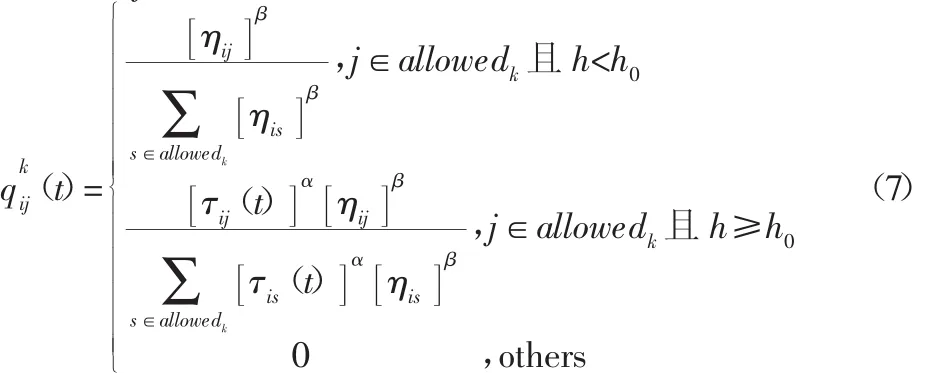
4.3 挥发系数自适应调整

信息素挥发系数ρ对算法性能影响很大，若信息素挥发系数过大，则蚁群对蚂蚁引导作用过小，蚁群的群体智能性无法显示出来；若信息素挥发系数过小，此时蚁群对蚂蚁的引导作用过强，使蚁群的搜索能力降低，可行解的搜索范围减小。因此提出了自适应的挥发系数调整方法，在算法的前期，挥发系数较低，减小蚂蚁之间的互相引导，增加蚂蚁的搜索范围，提高搜索效率；在算法后期，挥发系数较大，增加蚁群的群智能性，使算法快速收敛到最优解。基于以上分析，提出的挥发系数自适应调整方案为：

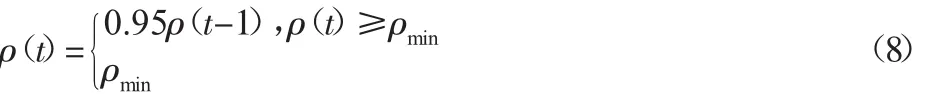
式中：ρmin—挥发系数ρ可以取到的最小值，挥发系数ρ初值为1。由式（8）可以看出，随着算法的进行，挥发系数不断减小，直至达到最小值。

4.4 基于改进遗传算法的机器人路径规划步骤

通过以上分析，基于改进遗传算法的机器人路径规划步骤具体为：Step1：参数初始化。需要初始化的参数包括种群个数n、最大迭代次数Kmax、信息启发因子α、期望启发因子β等、信息素感应阈值h0；Step2：将n/2只蚂蚁分别放置在起点和终点进行路径规划，按照式（8）对挥发系数自适应调整，按照式（7）进行路径选择，直至两组蚁群相遇；Step3：按照式（6）选择最短路径，并记录最优路径，按照式（3）、式（4）、式（5）进行信息素更新；Step4：判断算法循环次数是否达到上限，若是则输出最优路径，否则将蚂蚁重新分组后返回Step2。

5 仿真实验

机器人的工作环境建模为（20×20）的栅格，传统蚁群算法和改进蚁群算法的蚁群规模均设置为30，算法的最大迭代次数设置为300。传统算法和改进算法最小路径长度随算法迭代次数的变化曲线，如图3所示。由图3可以得出两点结论：（1）改进算法相比于传统算法的收敛速度快很多，这是因为改进算法提出了信息素挥发因子，使算法在后期能够快速收敛至最优解；再者对式（5）进行了重新定义，保留了种群对最优路径的记忆能力，促进了算法的快速收敛；再就是使用了蚂蚁相遇策略，蚁群能够相向同时进行路径搜索，提高了搜索效率。（2）改进算法最终的收敛值明显优于传统算法，这是因为改进算法提出了自适应信息素挥发因子和设置了信息素感应阈值，使算法在前期能够大范围地对解空间进行搜索，使得改进算法搜索到的最优解优于传统算法。

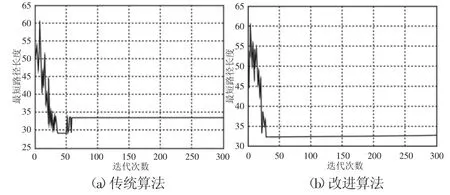
图3 最短路径长度变化曲线Fig.3 Length Changing Curve of Shortest Path

如图4所示，一次路径规划中全部蚂蚁的规划结果，从图中可以看出，改进算法中蚂蚁的规划路径非常集中，集中在最优路径附近，而传统算法的路径相对分散，没有很好的集中在最优路径附近。这说明改进算法的蚁群在进行路径搜索时，目标比较明确，减少了算法在路径搜索时的盲目性。这是因为对式（5）进行重新定义，保留了蚁群对最优路径的“记忆”能力，使蚁群在路径搜索时目标明确，规划出的路径集中在最优路径附近。

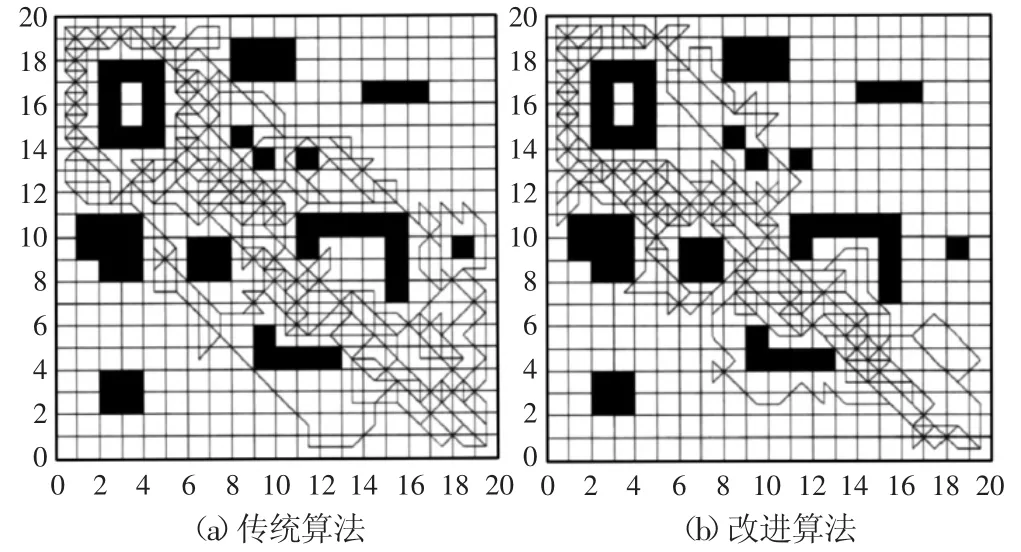
图4 所有蚂蚁的规划结果Fig.4 Planning Path of Every Ant

6 结论

通过以上分析，可以得到以下结论：（1）蚂蚁相遇策略使蚁群同时相向搜索，加快了算法的搜索速度；（2）蚂蚁回退策略可以避免蚂蚁陷入U形陷阱，增加了算法鲁棒性和适应性；（3）通过设置信息素敏感阈值，增加了算法前期的大范围搜索能力；（4）对信息素残留公式的重新定义，保留了算法对最优解的“记忆”能力，使蚁群搜索目标明确，规划出的路径集中在最优路径周围；（5）信息素挥发系数的自适应调整兼顾了算法前期的大范围搜索和后期的快速收敛；（6）与传统算法相比，改进遗传算法具有更快的收敛速度和更好的最优解。

［1］谭民，王硕.机器人技术研究进展［J］.自动化学报，2013，39（7）：963-972.（Tan Min，Wang Shuo.Research progress on robotics［J］.Acta Autom Atica Sinca，2013，39（7）：963-972.）

［2］栗红生，刘莹.复杂路径下机器人路径规划优化方法仿真［J］.计算机仿真，2014，31（1）：407-411.（Li Hong-sheng，Liu Ying.Robot path planning under complicated path simulation optimization method［J］.Computer Simulation，2014，31（1）：407-411.）

［3］Fakoor M，Kosari A，Jafarzadeh M.Humanoid robot path planning with fuzzy markov decision processes［J］.Journal of Applied Research&Technology，2016，14（5）：300-310.

［4］柴寅，唐秋华，邓明星.机器人路径规划的栅格模型构建与蚁群算法求解［J］.机械设计与制造，2016（4）：178-181.（Chai Geng，Tang Qiu-hua，Deng Ming-xing.Grid model and ant colony aligorithm for robot path planning［J］.Machinery Design&Manufacture，2016（4）：178-181.）

［5］李明磊，赵杰，李戈.面向方形节点拓扑地图下的移动机器人路径规划算法研究［J］.机械与电子，2015（10）：67-70.（Li Ming-lei，Zhao Jie，Li Wen.Research on pathh panning algorithm for mobile robot based on square nades in topological map［J］.Machinery&Electronics，2015（10）：67-70.）

［6］陈超，唐坚，靳祖光.一种基于可视图法导盲机器人路径规划的研究［J］.机械科学与技术，2014，33（4）：490-495.（Chen Chao，Tang Jian，Zhan Zu-guang.A path planning algorithm for seeing eye robots based on V-Graph［J］.Mechanical Science and Technology for Aerospace Engineering，2014，33（4）：490-495.）

［7］卢路秋.基于模糊人工势场法的多移动机器人路径规划研究［D］.天津：天津工业大学，2016.（Lu Lu-qiu.Based on the fuzzy artificial potential field method of multi mobile robot path planning research［D］.Tianjing：Tianjin University of Technology，2016.）

［8］李刚，鱼佳欣，郭道通.基于改进遗传算法的机器人路径规划与仿真［J］.计算技术与自动化，2015（2）：24-27.（Li Gang，Yu Jia-xin，Guo Dao-tong.Robot path planning based on improved genetic algorithm and simulation，2015（2）：24-27.）

［9］乔茹，章小兵，赵光兴.基于改进蚁群算法的移动机器人全局路径规划［J］.安徽工业大学学报：自科版，2009，26（1）：77-80.（Qiao Ru，Zhan Xiao-bing，Zhao Guang-xing.Global path planning of mobile robot based on improved ant colony algorithm［J］.J.of Anhui University of Technology，2009，26（1）：77-80.）

［10］Zhang K，Yuan C M，Gao X S.A greedy algorithm for feedrate planning of CNC machines along curved tool paths with confined jerk［J］.Robotics and Computer-Integrated Manufacturing，2012，28（4）：472-483.