某重卡动力总成悬置系统稳健性优化设计
胡新强 ,刘建勋 ,陈国栋 ,贺新峰
(1.湘潭大学 机械工程学院,湖南 湘潭 411105;2.株洲时代新材料科技股份有限公司,湖南 株洲 412007)
1 引言
动力总成悬置系统是动力总成与车架/车身相连的振动系统,主要有支撑、隔振、限位的作用,对整车NVH性能提升起着非常大的作用。合理的悬置系统设计,不但可以降低整车振动与噪声,而且能改善乘车舒适性,提高零件、部件和整车的耐久性[1]。
目前,国内外研究者大部分采用传统确定性方法对悬置系统进行优化设计,即悬置刚度、阻尼和安装角度等可控。但悬置产品刚度存在材料、制造、加工、测量等因素影响而产生上下波动,从而影响系统NVH性能,甚至导致设计失效。因此,在悬置系统初期设计阶段对系统进行稳健性分析和优化是非常必要。文献[1]中采用灵敏度方法为悬置系统的解耦布置、鲁棒设计提供参考;文献[2]采用蒙特卡罗方法对悬置系统稳健性设计,提高了产品设计的合格率。文献[3]中利用6sigma优化方法对动力总成悬置系统的固有频率、频率间隔和解耦率的性能参数进行稳健性优化,保证了设计要求。
以某四点重卡悬置系统为研究对象,对系统进行稳健性分析和优化。以悬置刚度为设计变量,固有频率合理配置为约束,以解耦率为目标,采用命令流方式用Isight集成ADAMS/View建立参数化模型对悬置刚度进行确定性优化,解耦优化取得了很好的效果,满足系统隔振性能要求;然后采用具有正态分布来描述设计变量的波动,对确定性优化进行稳健性分析;针对确定性优化的系统NVH性能参数稳健性差的问题,利用6sigma稳健性优化方法对系统进行优化,稳健性优化后系统的NVH性能稳健性明显提高。
2 悬置系统解耦设计
首先对悬置系统进行简化,把动力总成看作刚体;把橡胶悬置简化为三个相互垂直的线性弹簧;悬置阻尼很小,系统设计可以忽略[4],因此把悬置系统简化成,如图1所示。已知X轴沿着曲轴方向指向发动机前端,Z轴垂直地面向上,Y轴遵循右手定则,则可以建立振动方程:Mq¨+Kq={0} (1)式中:M—动力总成系统质量惯性矩阵;K—悬置系统刚度矩阵;
q¨,q—分别为系统加速度、坐标矢量。
求(1)中悬置系统固有频率ω 和振型 φ:{K-ω2M}φ=0 (2)
通常悬置系统存在耦合,当某一个振型方向激励会引起其他振型方向产生振动。这种振动耦合对整个系统不利的,它不仅会引起悬置系统共振,而且加大悬置系统频率频宽,从而对隔振设计带来麻烦。因此,需要避免或减少耦合现象发生。解耦设计是提高隔振系统性能的最有效途径之一。

图1 动力总成悬置系统模型Fig.1 Dynamic Model of Powertrain Mount System
能量解耦率表达式[5]:
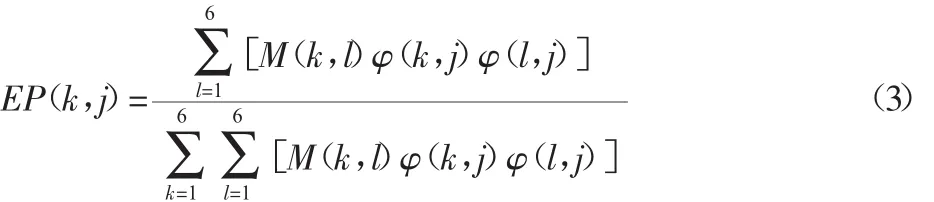
EP(k,j)=100%时,表示第j阶模态振动,则能量全部集中在第k个坐标上,则其他方向能量为0。
3 6sigma稳健性优化理论
6sigma设计方法[6]从统计学的角度出发,在设计阶段引入概率模型分析不确定性对产品的性能和质量的影响,借助于概率分析方法来控制变量设计出满足性能、可靠性和成本的高性能产品。6sigma设计的目标是设计空间内要满足设计性能要求,又要提高产品可靠性。6sigma优化中,通过改进设计参数的均值或方差,能有效地降低产品失效概率,提高产品的可靠性和稳健性,如图2所示。
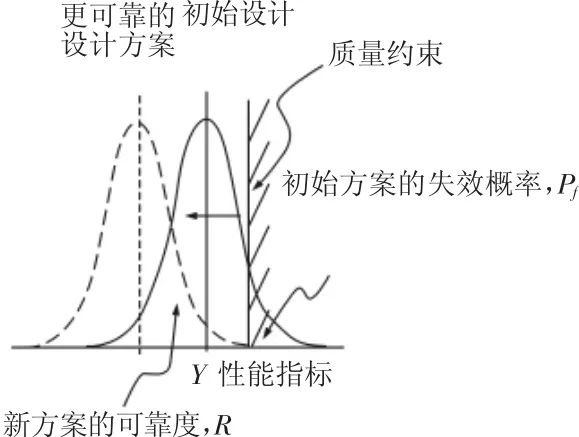
图2 提高设计方案的可靠性和质量水平Fig.2 Improve the Reliability and Quality Level of Design
6sigma稳健性优化是将确定性优化问题转换为DFSS问题数学模型:
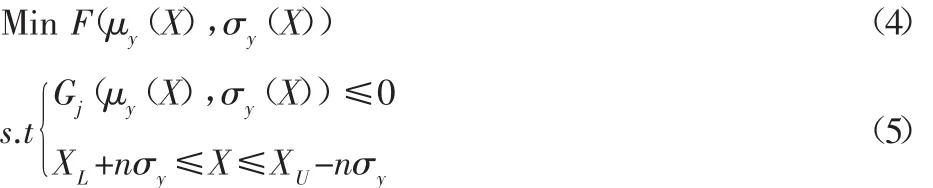
式中:X—设计变量;j—约束变量的个数;XL、XU—约束的下限、上
限;μy—X 的均值;σy—X 的方差;F—目标函数。
6sigma稳健性优化目标包括“达到平均性能目标”和“最小性能波动”,因此稳健性的目标函数:
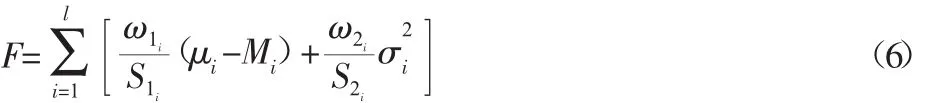
式中:ω1i、ω2i—权函数;S1i、S2i—比例因子;Mi—设计目标 μi的指定值;l—设计目标的个数。
动力总成悬置系统的稳健性优化设计流程,如图3所示。

图3 悬置系统稳健性优化设计流程Fig.3 Robustness Optimization Design Process of Powertrain Mount System
4 应用实例
4.1 确定性优化设计及其稳健性分析
已知某重卡四点悬置动力总成,其发动机为四缸四冲程,其怠速工况下的转速为800r/min,现有发动机的质量为m=820kg,其他参数,如表1所示。在ADAMS/View中建立悬置系统动力学模型。

表1 动力总成质量参数Tab.1Quality Parameters of Powertrain Mount System
4.1.1 设计变量和约束条件
动力总成悬置系统的固有频率及解耦率与动力总成惯性参数、悬置位置、刚度和阻尼以及安装角度等密切有关。由于整车布置受限,悬置位置和安装角度很难调整,文中只考虑悬置刚度进行确定性优化。选取四个悬置主刚度作为设计变量,约束范围为-(80~80)%。
在确定性优化设计中,主要振动方向Bounce和Roll解耦率要求>80%;其他方向解耦率要求>75%。
为了保证悬置系统的固有频率在合理配置区间内,根据隔振理论,则要求系统的最高频率小于18.9Hz;其次,悬置系统要避开路面激励(通常大于5Hz),故悬置系统固有频率范围为(5~18)Hz。另外,为了避免悬置系统频率之间发生共振,则频率间隔要求1Hz左右;Bounce频率应避开车身和前桥的垂直跳动固有频率(一般在(5~7)Hz左右[7]),同时还要避免人体最敏感的垂直振动频率(4~6)Hz,以及前悬的同步跳动,避免车架一阶扭转、一阶弯曲等固有频率。综上所述,系统约束条件,如表2所示。

表2 动力总成悬置系统频率和解耦率要求Tab.2 Basic Requirements for Natural Frequencies and Decoupling Rate of Powertrain Mount System
4.1.2 目标函数
悬置系统的解耦设计优化是一个复杂的多目标优化问题,采用加权法,把多目标优化问题转化为单目标优化问题,建立目标函数如下:

式中:Fi—第i阶模态的解耦率;wi—权重因数;F—优化目标函数。
由于Bounce和Roll方向为系统的主要振动方向,则Bounce和Roll方向的解耦率的权重系数为1.2,其余方向解耦率的权重系数为1.0。
采用序列二次规划算法对悬置刚度进行优化,获得了确定性优化固有频率和解耦率,如表3所示。优化后的固有频率范围为(5.30~17.34)Hz,满足固有频率要求,使振动特性得到很大改善;主要的振动Roll方向的解耦率从优化前的78.21%提高到94.24%;Bounce方向的解耦率有所提高。Yaw方向的解耦率从优化前的63.89%提高到98.76%,达到完全解耦;Pitch方向的解耦率从优化前的44.60%提高到93.66%,达到能够解耦;其它各项性能指标也满足设计要求。
4.1.3 稳健性分析
在悬置系统确定性优化中能够获得满足设计要求的解,当设计变量上下波动或偏差时,部分随机设计变量的解超出约束范围进入不可行区域,极易导致设计失效,因此需对悬置系统NVH性能进行稳健性分析。悬置刚度是NVH性能能最主要的影响因素之一,因此悬置设计过程中必须考虑刚度不确定性对系统NVH性能的影响。文中考虑悬置刚度波动误差为,其刚度服从以设计值为均值的正态分布的独立变量。基于命令流的方式Isight集成ADAMS的方法,将确定性优化下结果进行稳健性分析,获得了悬置系统性能的sigma水平和可靠度,如表3所示。并在Isight中提取了动力总成悬置系统第1阶和第6阶固有频率的3sigma水平,如图4、图5所示。由分析结果可知,虽然有些设计目标达到8sigma,但第1阶和第6阶固有频率的质量水平分别为2.32sigma和1.89sigma,其质量水平均不到3sigma,不满足设计要求,且第1阶固有频率稳健差,可能引起悬置产品的刚度过低,导致悬置产品的使用寿命和耐久性;第6阶固有频率稳健性差,会可能导致系统最高频率过高,将影响系统的NVH性能。综上所述,悬置系统NVH性能稳健性差,须对系统稳健性优化设计。

图4 确定性优化第1阶固有频率sigma水平Fig.4 Deterministic Optimization of the First Order Natural Frequency Sigma Level
图中:Probability—概率密度;f—频率,Quality—质量水平;Mean—均值;Std.Dev—方差;L.Bound—约束下边界;U.Bound—约束上边界,图5~图7中同上)。

图5 确定性优化第6阶固有频率sigma水平Fig.5 Deterministic Optimization of the Sixth Order Natural Frequency Sigma Level
4.2 稳健性优化设计
为了提高悬置系统的稳健性,采用6sigma稳健性优化方法做进一步优化[8-9]。而悬置产品在实际生产过程中所有设计目标达到6sigma水平,几乎不可能,但3sigma水平是工程设计可以达到值,因此把固有频率和解耦率的稳健优化的sigma水平设置为3[10]。根据悬置系统设计要求,选择悬置的刚度为随机变量,可以建立6sigma 稳健性优化的数学模型:Min:-u(F(x))+σ(F(x)) (8)

式中:fi—固有频率;Ei—解耦率。
通过6sigma稳健性优化,Isight中提取了第1阶和第6阶固有频率的sigma水平,如图6、图7所示。将确定性优化方案与稳健性优化方案对比,如表3所示。与确定性优化方案相比,稳健性优化方案的设计变量变化不大,这说明确定性优化附近存在性能相当的解,但其优化解的稳健性有一定的差距,稳健性优化后固有频率和解耦率满足设计要求,同时也满足隔振要求,并且稳健性优化后悬置NVH性能稳健性和可靠性显著提高。稳健性优化后的第1阶固有频率的sigma水平提高到3.19sigma,可靠度由97.98%提高到99.85%;主要振动方向Roll固有频率的sigma水平提高到3.2sigma,可靠度由94.25%提高到99.85%,优化后改善了系统隔振性能的稳健性,从而减小了系统的设计失效概率。
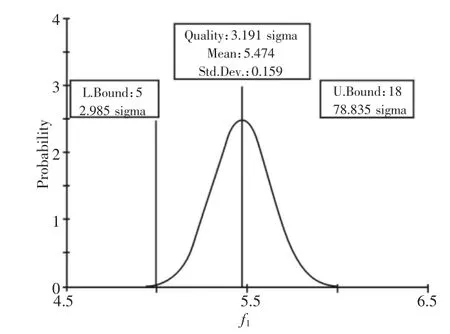
图6 稳健性优化第1阶固有频率sigma水平Fig.6 Robustness Optimization of the First Order Natural Frequency Sigma Level
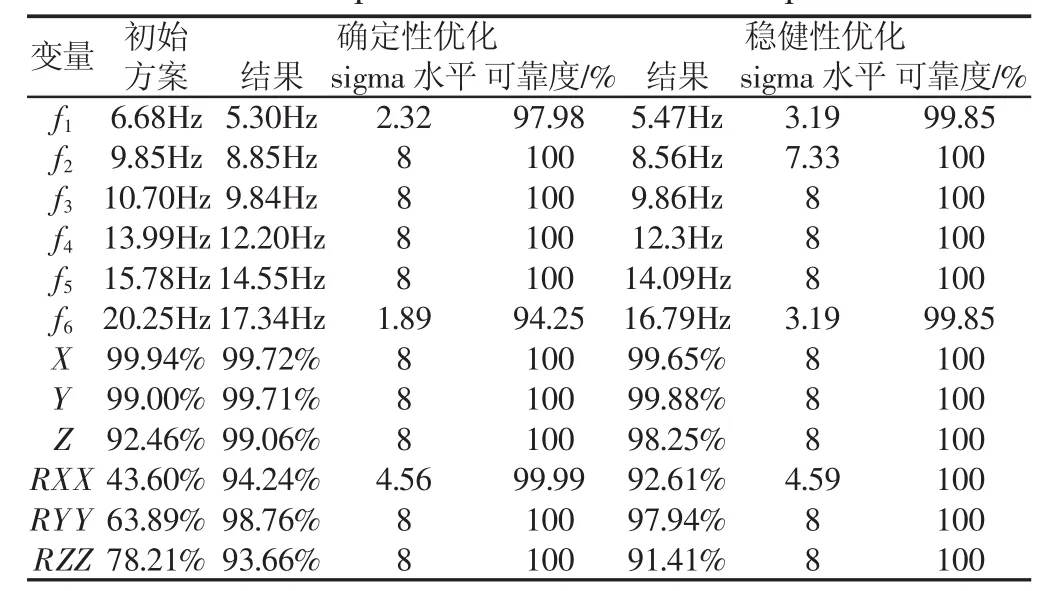
表3 确定性优化和稳健性优化质量水平和可靠度比较Tab.3 Comparison of Quality Level and Reliability of Deterministic Optimization and Robust Optimization

图7 稳健性优化第6阶固有频率sigma水平Fig.7 Robustness Optimization of the Sixth Order Natural Frequency Sigma Level
5 结论
针对某重卡四点悬置系统,建立ADAMS动力学模型,以命令流方式将Isight集成ADAMS对悬置系统进行稳健6sigma性优化,稳健性优化后第1阶频率(Lateral)从5.3Hz提高到5.47Hz,质量水平从2.32sigma提高到3.19sigma,从可靠度由97.98%提高到99.85%;第6阶频率(Roll)从17.34Hz下降到16.79Hz,质量水平1.89sigma提高到3.2sigma,可靠度由94.25%提高到99.85%;通过稳健性优化设计,可以综合考虑悬置刚度性能的波动(硬度、工艺和尺寸等引起波动)对系统NVH的影响,对提升悬置系统NVH性能的稳健性,具有实际的意义。
[1]张武,陈剑,陈鸣.采用正交试验的发动机悬置系统灵敏度分析[J].噪声与振动控制,2011(5):168-172.(Zhang Wu,Chen Jian,Chen Ming.Sensitivity analysis of engine’s mounting system based on orthogonal experiments[J].Noise and Vibration Control,2011(5):168-172.)
[2]时培成,陈无畏,高立新.基于蒙特卡罗法的动力总成悬置系统稳健性设计[J].汽车工程,2010(8):707-711.(Shi Pei-cheng,Chen Wu-wei,Gao Li-xin.Robustness design of powertrain mount system based on monte carlo method[J].Automotive Engineering,2010(8):707-711.)
[3]吴杰,上官文斌.基于的动力总成悬置系统鲁棒优化设计[J].振动与冲击,2008(8):64-67.(Wu Jie,Shangguan Wen-bin.Robust optimization design of powertrain mount system based on six sigma[J].Journal of Vibration and Shock,2008(8):64-67.)
[4]范让林,黄元毅.汽车动力总成-悬置系统的简化及其启发[J].机械设计与制造,2010(4):8-10.(Fan Rang-lin,Huang Yuan-yi.The simplification of automotive powertrain mounting system and its Illuminations[J].Machinery Design&Manufacture,2010(4):8-10.)
[5]李令兵,陈剑,吴赵生.基于ADAMS的发动机悬置系统设计[J].噪声与振动控制,2007(6):42-44.(Li Ling-bing,Chen Jian,Wu Zhao-sheng.Design of the engine mounting system based on ADAMS[J].Noise and Vibration Control,2007(6):42-44.)
[6]赖宇阳.Isight参数优化理论与实例详解[M].北京:北京航空航天大学出版社,2012.(Lai Yu-yang.Isight Parameter Optimization Theory and Example Explanation[M].BeiJing:Beihang University Press,2012.)
[7]庞剑,谌刚,何华.汽车噪声与振动—理论与应用[M].北京:北京理工大学出版社,2006.(Pang Jian,Shen Gang,He Hua.Automotive Noise and Vibration-Principle and Application[M].Beijing:Beijing Institute of Technology Press,2006.)
[8]Koch P N,Yang R J,Gu L.Design for six sigma through robust optimization[J].Structural and Multidisciplinary,2004,26(3-4):235-248.
[9]Qatu M,Sirafi M,Johns F.Robustness of powertrain mount system for noise,vibration and harshness at idle[J].Proceedings of the Institution of Mechanical Engineers,Part D:Journal of Automobile Engineering,2002,216(10):805-810.
[10]侯勇,赵涛.动力总成悬置系统解耦设计[J].汽车工程,2007(12):1094-1097.(Hou Yong,Zhao Tao.A study on decoupling design of engine mounting system[J].Automotive Engineering,2007(12):1094-1097.)

