基于改进NSGA-Ⅱ算法的发动机活塞机构优化设计

夏尔冬 ，王春荣 ，2，熊昌炯 ，刘建军

（1.三明学院机电工程学院，福建 三明 365004；2.北京工业大学机械工程及应用电子技术学院，北京 100124）

1 引言

发动机[1-3]是汽车的动力来源，是汽车中最重要的部分，其性能直接影响汽车的动力、油耗、排放等，而活塞机构是发动机中重要的运动部件之一，活塞机构的运动速度、加速度、运动轨迹等决定对发动机的性能。因此，对活塞机构进行优化设计研究，具有十分重要的意义。

国内外有些学者已对活塞机构展开了相关研究，文献[4]借助Pro/E对曲柄活塞机构的运动进行了仿真研究；文献[5]用ADAMS对柴油机的曲柄两活塞机构进行了动力学分析，得到了工作中曲柄的危险位置；文献[6]对发动机的活塞机构各杆长进行研究，但只考虑了其跟踪误差，却忽略了传动角对其运动性能的影响。

以活塞机构的运动轨迹误差和传动角与90°偏差为双目标优化函数。传统的多目标优化是利用加权法将多目标转化为单目标进行优化，但是由于权系数的主观因素太强，对优化性能具有很大的影响[7]。利用NSGA-Ⅱ算法[8-12]对活塞机构进行双目标优化，为增强其搜索能力与种群多样性，对NSGA-Ⅱ算法进行了改进，采用改进的NSGA-Ⅱ算法对活塞机构进行优化设计分析，提高活塞机构的运动性能。

2 活塞机构数学模型建立

利用PRO/E对发动机活塞机构进行三维实体建模，如图1所示。包括活塞、曲柄、连杆等，对其进行运动分析，机活塞机构运动简图，如图2所示。

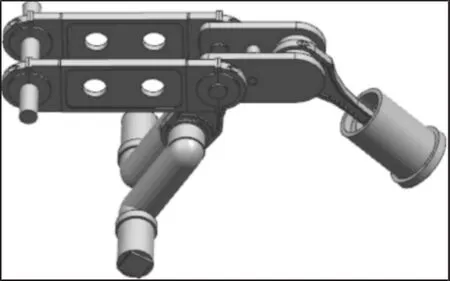
图1 发动机活塞机构三维模型Fig.1 The Three-Dimensional Model of Engine Piston Mechanism

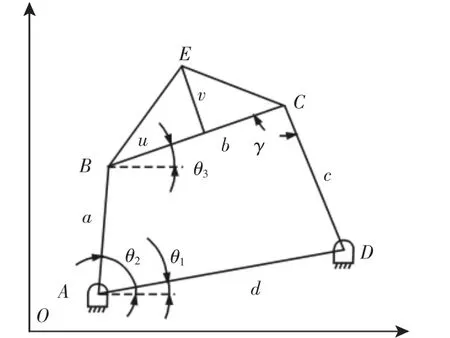
图2 机活塞机构运动简图Fig.2 The Motion Diagram of Piston Mechanism

2.1 目标函数的确定

（1）根据图2中几何关系，E点的坐标可以表示为：

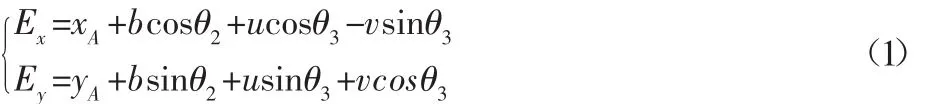
式中：（xi，yi），i=1，2，…，k—理论点的坐标，则 E 的轨迹误差函数为：

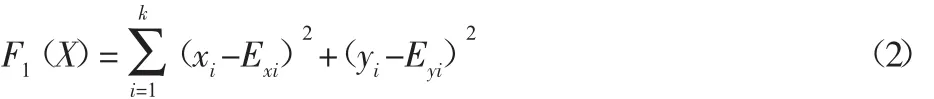
（2）在四连杆机构中传动角具有十分重要的作用，传动角越大、越接近90°表明机械系统的传动性能越好。图2中最大、最小传动角可以表示为：

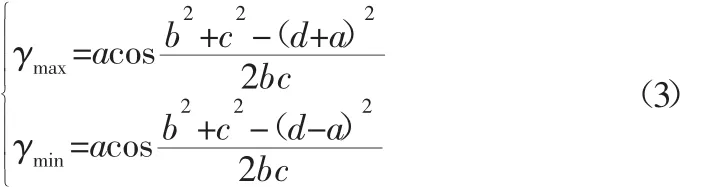
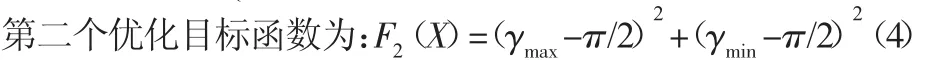
2.2 设计变量的确定

根据文献[13]可知θ3为θ2的函数，因此取设计变量为：

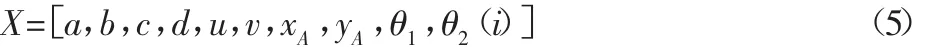
2.3 约束条件的确定

（1）四连杆曲柄机构，应满足各个杆长约束条件：

（2）边界约束条件：

3 改进算法

3.1 NSGA-Ⅱ简介

算法是文献[14]在算法基础上进行改进的，主要区别为了减小算法计算的复杂度引入了快速非支配排序法、利用拥挤度和拥挤度算子、代替共享参数σshare，并具有精英保留策略，提高种群的搜索空间，是一种处理多目标问题的优秀算法。然而直接采用算法对发动机活塞机构进行优化，发现Pareto最优解分别不够均匀，这是由于其在寻优过程中早熟收敛所引起的。为了提高种群的多样性、算法的搜索能力，使得Pareto最优解集更加均匀的分布，提出了对交叉算子和变异算子进行改进。

3.2 NSGA-Ⅱ的改进

自适应交叉算子与变异算子和传统的算法直接采用交叉概率PC和变异概率Pm不同，而是与个体的适应值相关。若个体的适应值比平均适应值小，此时为了尽量多的保留优秀的个体，应选用较小的PC和Pm；若个体的适应值比平均适应值大，此时为了生成下一代优秀的个体，应选用较大的PC和Pm；若种群中所有个体的适应值几乎相同时，此时为了使算法扩大搜索区域从局部最优中跳出，应使整体的PC和Pm较大；反之，种群中所有个体的适应值差距非常大，此时为了使算法尽快收敛，应使整体的PC和Pm较小，即：

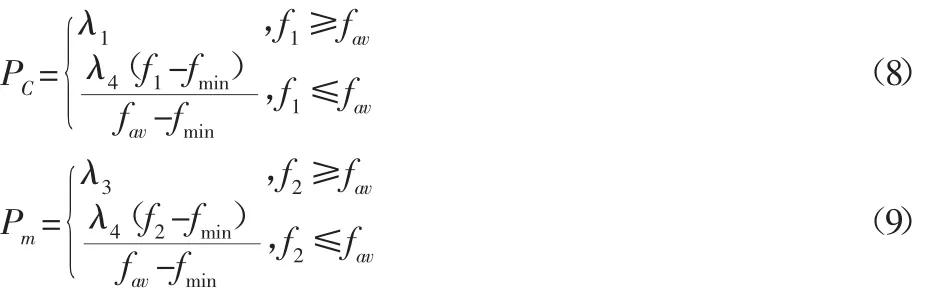
式中：f1、f2—交个体与变异个体的平均适应值；

fav、fmin—种群的平均和最小适应值，λ1，λ2，λ3，λ4∈［0，1］。

3.3 算法执行过程

所提出的算法的执行步骤，如图3所示。

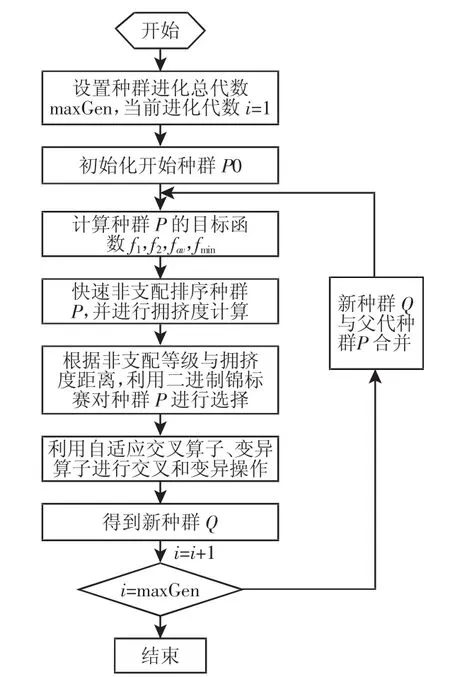
图3 改进算法流程图Fig.3 The Flow Chart of Improved NSGAⅡ

4 实验分析

给定目标轨迹坐标点与文献[6]相同，即（9.5，8.26），（9.0，8.87），（7.97，8.87），（5.65，9.94），（4.36，9.7），（3.24，9.0），（3.26，8.36），（4.79，9.11），（6.58，8.0），（9.12，7.87）；设计变量的取值范围为：xA，yA∈［0，5］，a，b，c，d，u，v∈［0，5］，θ1，θ2（i）∈［0，5］。

4.1 不同算法对比

分别采用传统的算法与改进的算法对发动机活塞机构进行优化，所求得的Pareto最优解集，如图4所示。两种算法所求得的的最小值与最大值，如表1所示。四种极值情况的轨迹曲线图，如图5所示。分析实验结果，可以明显的发现，改进的算法Pareto最优解的分布比传统算法较为均匀且具有较快的收敛速度，即提出的改进算法提高种群的多样性、算法的搜索能力。所改进的算法，得到的最值比传统算法小，具有较好的优化性能。分析图5、图6不难发现，改进的算法所得到的轨迹比传统算法的轨迹更加接近理论轨迹。

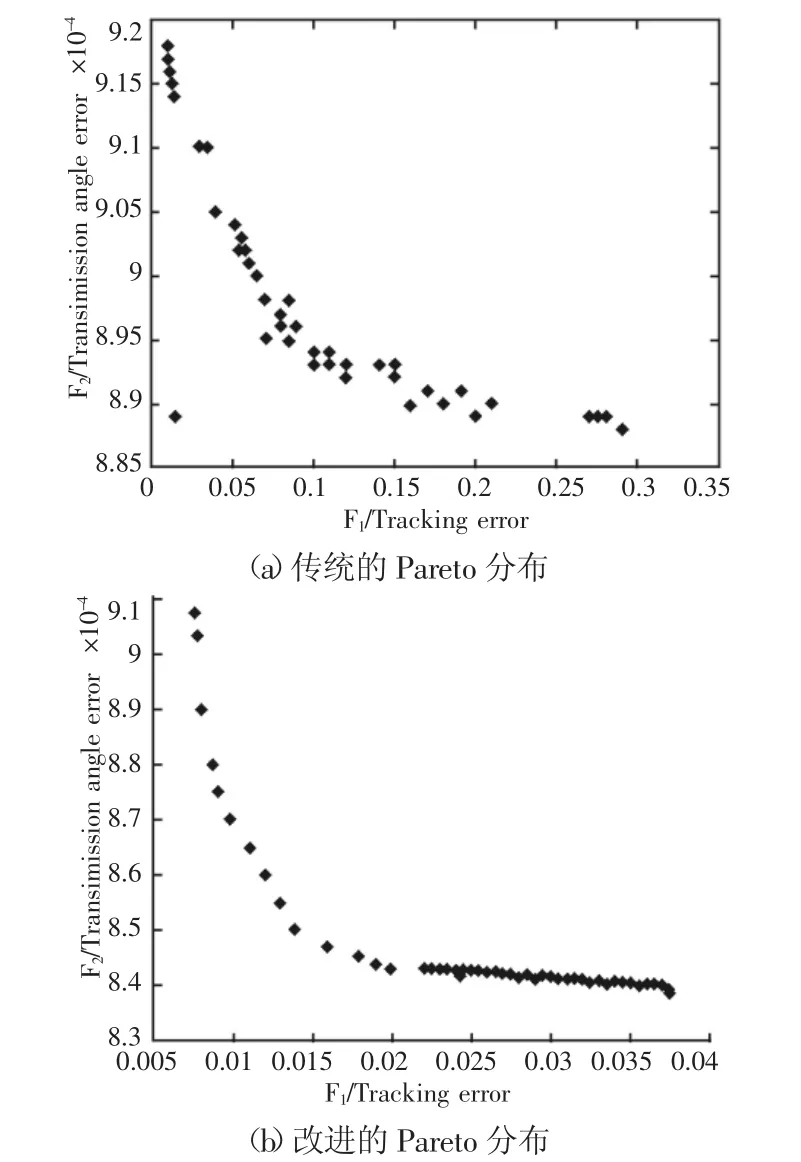
图4 Pareto最优解的分布情况Fig.4 The Distribution of Pareto Optimal Solutions

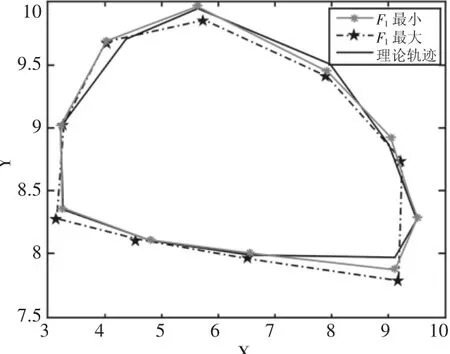
图5 传统轨迹图Fig.5 The Track Diagram of Traditional NSGAⅡ

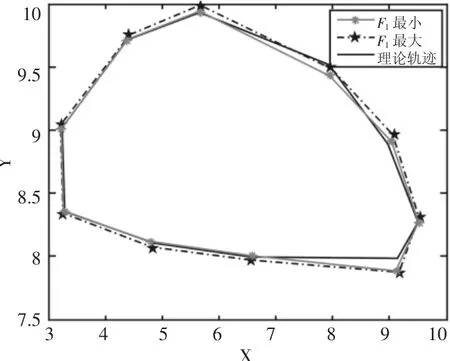
图6 改进轨迹图Fig.6 The Track Diagram of Improved NSGAⅡ

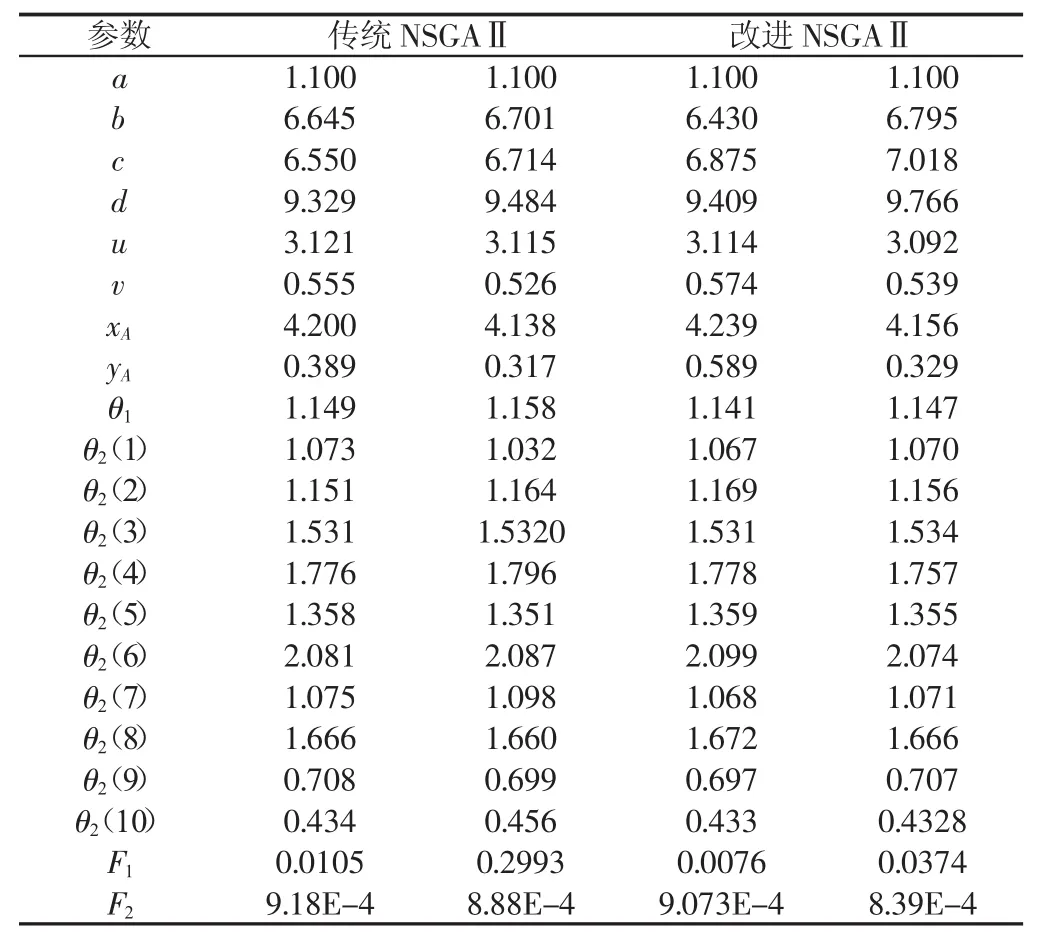
表1 Pareto解集中极值比较Tab.1 The Extreme Comparison of Pareto Solutions

4.2 最优Pareto解对比

Pareto解集中的每个解对于F1、F2都是相互冲突的，因此采用逼近理想解排序法从图4中的Pareto前沿选出两种算法各自的最优解进行比较，如表2所示，两种算法最优解的轨迹图，如图7所示。

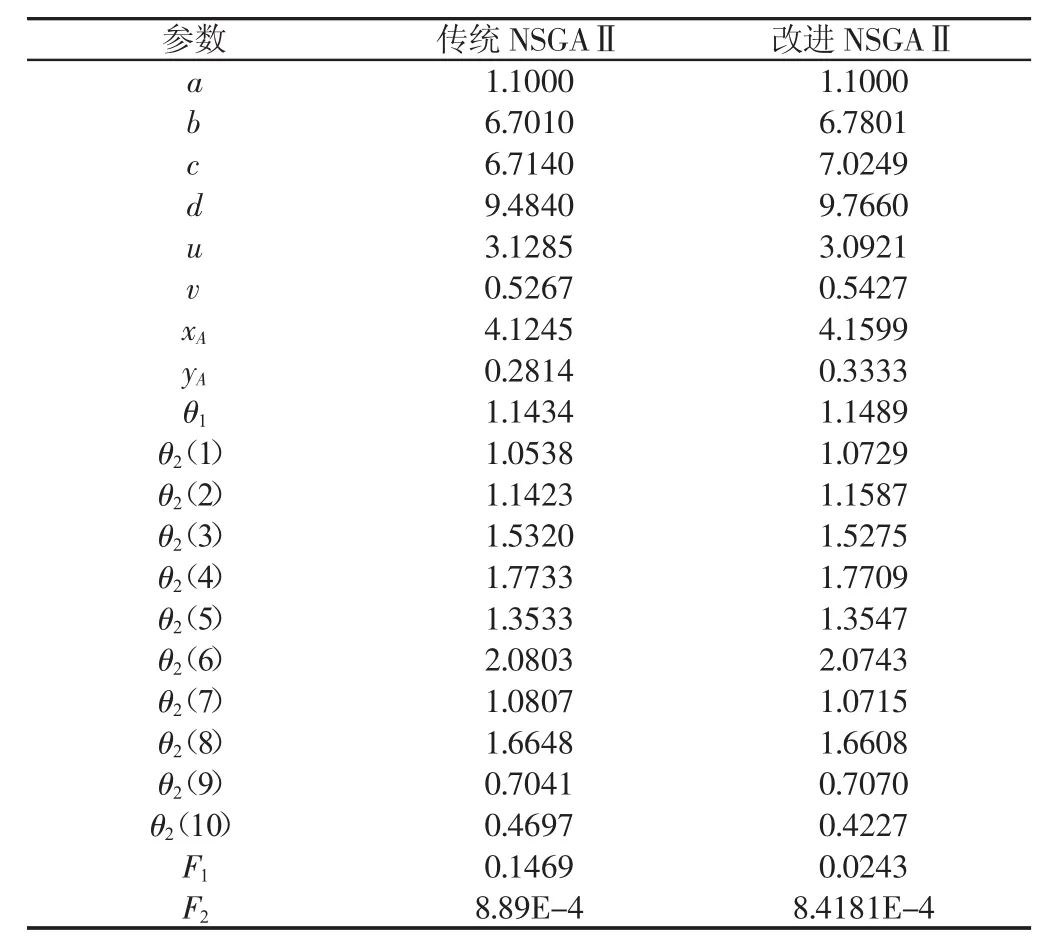
表2 Pareto解集的最优解比较Tab.2 The Optimal Solution Comparison of Pareto Solutions

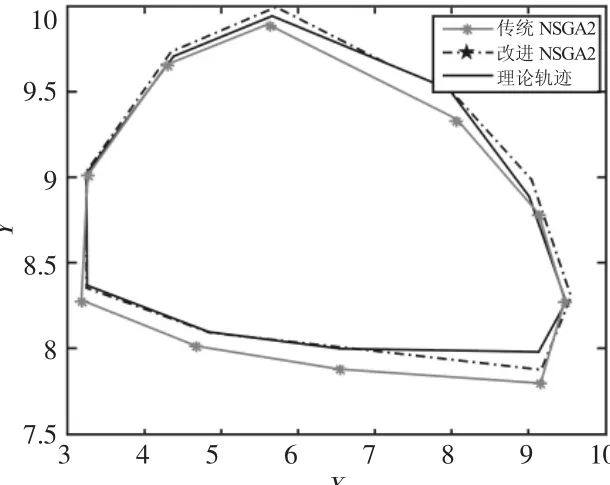
图7 最优解的轨迹对比图Fig.7 The Track Contrast Diagram of Optimal Solution

具体的实施过程为：

（1）归一化处理。将两种算法的F1、F2对应的值进行归一化，即：

式中：F1j、F2j—F1、F2目标函数得第 j个值。

（2）选出最优解。分别计算Pareto解集中的每个解与两个虚拟极端解的距离，距离越大代表此解越差，反之则为最优解，具体第k个解的距离dk为：

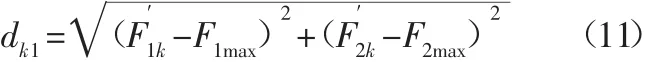
式中：dk1dk2—与两个极端解的距离。

对比实验结果表明，改进的算法比传统算法以及文献[6]的跟踪精度高，证明提出的改进算法具有较好的优越性。

5 结论

针对汽车发动机的重要零部件-活塞机构的运动性能进行了优化。提出以轨迹跟踪误差和传动角与直角的偏差为优化目标，采用改进的NSGAⅡ算法对活塞机构进行优化设计，结果表明所提出的改进算法可以用于活塞机构的多目标优化分析，并比传统的算法具有更好种群的多样性、搜索能力、更高的精度和更好的运动性能。

［1］熊建，顾宏.一种高可靠共轨柴油发动机电控单元［J］.大连理工大学学报，2016（1）：1-8.（Xiong Jian，Gu Hong.A highly reliable ECU of common rail diesel engine［J］.Journal of Dalian University of Technonlgy，2016（1）：1-8.）

［2］胡启国，周亨，罗天洪.大型矿车发动机橡胶悬置静、动态刚度特性研究［J］.机械设计与制造，2015（12）：213-215+220.（Hu Qi-guo，Zhou Heng，Luo Tian-hong.Analysis of static and dynamic characteristics of rubber mounts of large dump truck［J］.Machinery Design＆ Manufacture，2015（12）：213-215+220.）

［3］刘晓明，杨晓翔，韦铁平.发动机飞轮壳强度有限元分析［J］.机械设计与制造，2015（11）：239-242.（Liu Xiao-ming，Yang Xiao-xiang，Wei Tie-ping.Strength analysis of engine’s flywheel housing based on FEM［J］.Machinery Design ＆ Manufacture，2015（11）：239-242.）

［4］王果，卫瑞元，胡继雪.基于Pro/E的曲柄活塞机构的运动仿真分析［J］.苏州大学学报：工科版，2012（4）：66-70.（Wang Guo，Wei Rui-yuan，Hu Ji-xue.Analysis on motion simulation of the crank-piston mechanism based on Pro/E［J］.Journal of School Uninversity：Engineering Science Edition，2012（4）：66-70.）

［5］宇文志强.某新型柴油机曲轴连杆活塞机构动力学仿真分析［D］.东北大学，2011.（Yuwen Zhi-qiang.Dynamic simulation and analysis of crankshaft system in a new diesel engine［D］.Nourtheastern University，2011.）

［6］刘小月，木合塔尔·克力木，巨刚.基于ANSYS的曲柄摇杆机构的优化设计［J］.新疆大学学报：自然科学版，2015（2）：248-252.（Liu Xiao-yue，Muhetaer Kelimu，Ju Gang.Optimization design of crank rocker mechanism based on ANSYS［J］.Journal of Xinjiang University：Natural Science Edition，2015（2）：248-252.）

［7］李白雅，姜柏庄，龚明.基于PSO算法优化的机械臂轨迹规划研究［J］.信息技术，2014（9）：20-23+32.（Li Bai-ya，Jiang Bo-zuang，Gong Ming.Trajectory planning optimization of manipulator based on the PSO algorithm［J］.Information Technology，2014（9）：20-23+32.）

［8］陈鸿海，蒋增强，左乐.近亲变异NSGA-Ⅱ算法求解多目标柔性作业车间调度问题［J］.农业机械学报，2015（4）：344-350.（Chen Hong-hai，Jiang Zeng-qiang，Zuo Le.Multi-objective flexible jobshop scheduling problem based on NSGA-Ⅱwith Close relative variation［J］.Journal of Agricultural Machinery，2015（4）：344-350.）

［9］彭建刚，刘明周，张铭鑫.基于改进非支配排序的云模型进化多目标柔性作业车间调度［J］.机械工程学报，2014（12）：198-205.（Peng Jian-gang，Liu Ming-zhou，Zhang Ming-xin.Cloud model evolutionary multi-objective flexible job-shop scheduling based on improved non-dominated sorting［J］.Journal of Mechnical Engineering，2014（12）：198-205.）

［10］陈可嘉，周晓敏.多目标置换流水车间调度的改进食物链算法［J］.中国机械工程，2015（3）：348-353+360.（Chen Ke-jia，Zhou Xiao-min.Improved food chain algorithm for mutiobjective permutation flow shop scheduling［J］.China Mechanical Engineering，2015（3）：348-353+360.）

［11］王南，刘庆阳，周莎莎.基于Isight平台NSGA-Ⅱ方法的3-PRS并联机构多目标优化［J］.机械设计与制造，2015（12）：198-201.（Wang Nan，Liu Qing-yang，Zhou Sha-sha.Multi-objective optimization of 3-PRS parallel mechanism based on NSGA-Ⅱmethod of isight platform［J］.Machinery Design＆Manufacture，2015（12）：198-201.）

［12］周红妮，冯樱，胡群.多目标遗传算法NSGA-Ⅱ在某双前桥转向机构优化设计中的应用［J］.机械设计与制造，2015（11）：140-143.（Zhou Hong-ni，Peng Yin，Hu Qun.Application of multi-objective genetic algorithm NSGA-II in optimal design on a dual-front-axle steering mechanism［J］.Machinery Design＆Manufacture，2015（11）：140-143.）

［13］K.J.Waldron，G.L.Kinzel，Kinematics，Dynamics，and Design of Machinery［M］.2nd edition John Wiley&Sons Inc，2004.

［14］DEB K，PARTAP A，AGARWAL S.A fast and elitist multi-objective genetic algorithm：NSGA-Ⅱ［J］.IEEE Transactionson Evolutionary Computation，2002，6（22）：182-197.