汽车变速箱换挡比例电磁阀的磁场仿真研究

潘运平，吴仕凡，余先谋

（武汉理工大学 机电工程学院，湖北 武汉 430070）

1 引言

随着自动变速箱的日渐普及，双离合（DCT）变速箱以其换挡时间短、动力损失小、油耗低等优势在自动变速箱中脱颖而出，受到汽车公司的青睐。而比例电磁阀是DCT变速箱中的关键零部件，能够通过控制阀口开度来控制油压，实现换挡功能[1]。其静态电磁力特性和动态电流特性是电磁阀的两个重要特性，分别影响变速箱的换挡精度和开启时间。因此，对电磁阀的电磁力特性和电流特性研究具有重要意义。

目前，对于比例电磁阀的研究，文献[2-3]分析了隔磁环位置和角度、衔铁长度等结构参数对静态电磁力特性的影响，但并未就其动态特性进行讨论；文献[4-6]分析了不同线圈匝数等参数对电磁阀动态特性的影响，缺少对静态特性的分析；文献[7]通过分析隔磁角、衔铁长度等结构参数对电磁阀静态和动态特性的影响，研制出新型可变气门电磁阀，然而未详细探讨隔磁环位置、衔铁厚度等因素的影响。针对比例电磁阀在DCT变速箱上的性能要求以及综合考虑上述文献研究的不足之处，建立DCT换挡比例电磁阀的数学模型，利用AnsoftMaxwell对线圈匝数、隔磁槽位置、动铁芯厚度等重要参数进行仿真分析，研究其对静态电磁力特性和动态电流特性的影响。

2 原理分析

2.1 电磁阀结构及工作原理

DCT换挡比例电磁阀的结构图，如图1所示。其电磁部分由线圈、线圈骨架、静铁芯、动铁芯、外壳、垫圈构成。具体材料及参数，如表1、表2所示。

图1 电磁阀结构图Fig.1 Structure of Solenoid Valve

表1 电磁阀各部件材料Tab.1 Solenoid Valve Elements’Materials

表2 电磁阀相关参数Tab.2 Parameters of Solenoid Valve

2.2 理想电磁阀电磁力特性曲线

电磁阀在工作过程中阀芯受到弹簧力Fk、液压力Fl、摩擦阻力Ff以及来自于动铁芯的推力Ft，而推力Ft主要来自于动铁芯所受的电磁力Fm并与其近似相等，由此可以列出阀芯到达平衡位置时的方程：

电磁铁所受电磁吸力[8]：

由毕奥-萨伐尔定律[9]：

式中：φ—磁通量；B—磁感应强度；μ0—真空磁导率；S—磁路截面积；B—载流导线产生的磁场强度；μ0—真空磁导率；l—导线长度；I—通过导线的电流；er—电流元矢量。

因为在变速箱换挡时电流大小会发生相应的变化，由式（2）、式（3）可知，电磁力Fm的大小也会随之而变，此时阀芯会因为受力不平衡而开始运动并在弹簧的作用下运动至下一个平衡点，该平衡点即对应待换挡位所要求的阀口开度。在达到平衡之前，弹簧力Fx、液压力Fl会不断地变化直到与电磁力Fm相平衡（阀芯在运动时所受的摩擦阻力变化不大，故无须考虑），而阀芯在运动时也会引起动铁芯工作气隙的变化，如果工作气隙对电磁力Fm大小产生较大影响，则会使Fm产生较大波动，这必然导致阀芯运动到平衡点的位置产生较大偏差，阀口开度大小就会受到影响，出油口的压力大小便会发生波动，进而无法准确对应换挡油路，降低换挡精度。理想电磁阀的电磁力随工作气隙变化特性的曲线[5]，如图2所示。区域Ⅱ为工作行程区，此区域内电磁力变化越平稳，则其受工作气隙变化的影响就越小，换挡精度就越高。

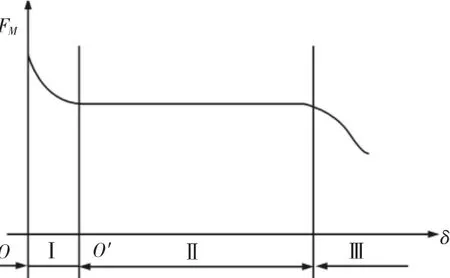
图2 理想电磁阀的电磁力特性曲线Fig.2 Ideal Electromagnetic Force Property Curve of Solenoid Valve

2.3 典型电流特性曲线

典型电流变化曲线[6]，如图3所示。图中：t0—动铁芯开始运动的时刻，称之为触动点；t1—电磁阀完全开启的时刻，称之为开启点。

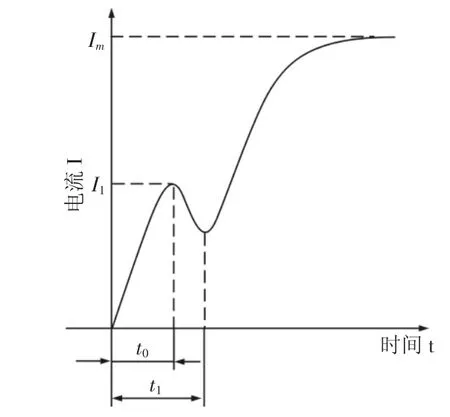
图3 典型电流特性曲线Fig.3 Typical Current Property Curve

3 有限元建模及仿真

3.1 静态磁场分析3.1.1有限元建模

宏观电磁场的有限元分析主要是基于麦克斯韦方程组，其在恒定磁场下的微分形式[8]如下：▽×H=J；▽×B=0 （4）（5）式中：H—磁场强度；B—磁感应强度；J—电流密度。

此外，磁场边值问题的求解，还需依据媒质的成分方程，对于各向同性媒质，其成分方程为：B=μH （6）式中：μ—磁导率

式（8）即为矢量磁位A所表示的磁场微分方程。因为铁芯材料为工业纯铁，属于铁磁媒质，故μ≠常数[9]。根据矢量分析有：

由于电磁阀结构为轴对称，故可将其简化为圆柱坐标系下的二维轴对称模型[10]，则式（10）可以转化为：

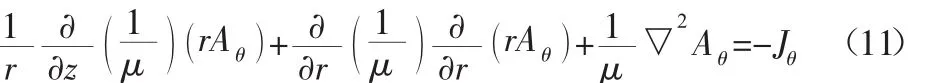
设该圆柱坐标系平面上的轴对称恒定磁场域为D，在非线性媒质中，Aθ满足泊松方程边值问题，即：

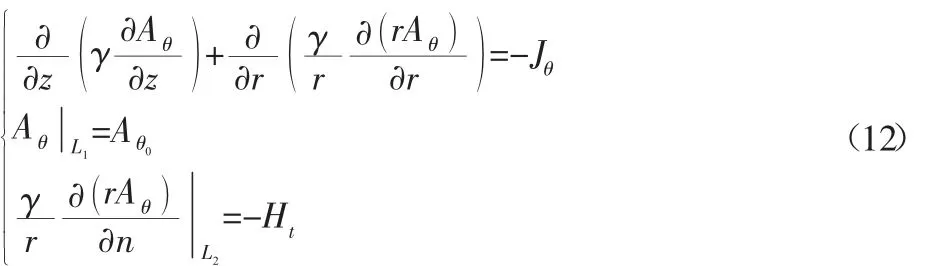
将式（12）导出有限元方程组，在式（12）中的第二式两端乘上 r，并令 γ′=，则式（12）变为：

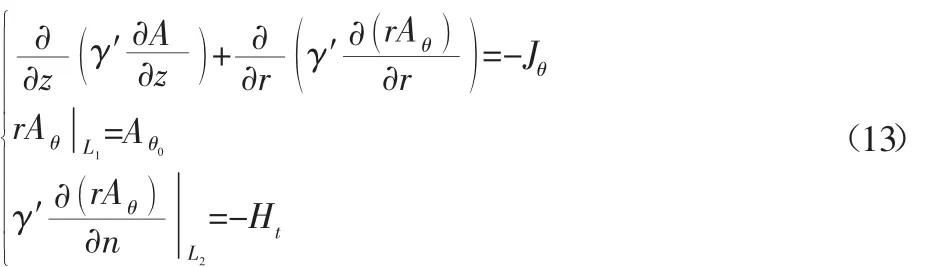
这时，将rAθ作为求解变量，转化为等价变分问题，在第二类边界条件（Neumann边界）下对应的泛函为：

式中：u=rAθ；

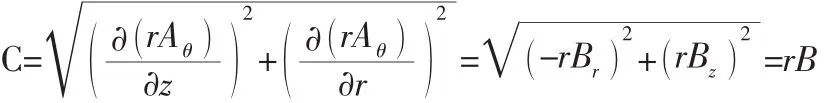
接下来对域进行剖分和插值，把泛函的变分问题转化为多元函数求极值的问题，从而得到电磁场定解问题的数值解。在计算出各节点磁位值后，结合虚功原理，得到铁芯受到的电磁力[11]，此处不再详述。依据上述理论在Ansoft Maxwell中实现仿真。由于重点研究对象为电磁阀的电磁部分，故在圆柱坐标系下建立简化后的电磁阀二维模型，如图4所示。并按照表1、表2所给的电磁阀实际结构参数和材料设置其属性，求解区域的边界条件设置为Ballon（Neumann边界为系统默认，故无需手动设置），网格划分按默认设置。为分析线圈匝数、隔磁槽位置、动铁芯厚度对电磁力特性的影响，分别将这三个参数设为变量，进行变参数仿真求解。

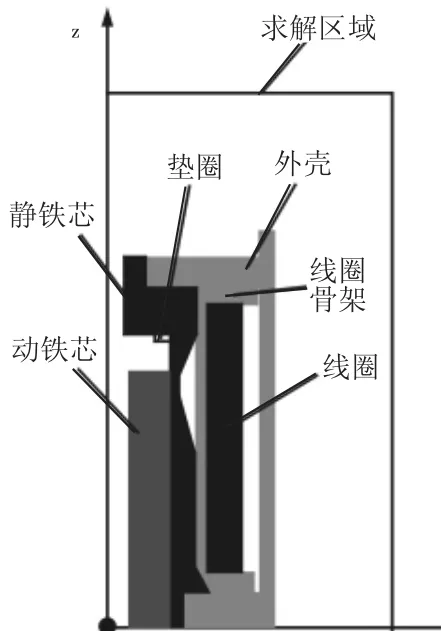
图4 电磁阀二维仿真模型Fig.4 2D Simulation Model of Solenoid Valve

3.1.2 线圈匝数对电磁力特性的影响

隔磁槽位置、动铁芯厚度不变，仅变化线圈匝数，变化范围为［112，1012］，步长为100。仿真得出不同线圈匝数下的电磁力特性曲线，如图5所示。从仿真结果可以看出，随着线圈匝数的增大，电磁力特性曲线的工作行程区由平稳逐渐变得凸起，线圈匝数在［212，615［时最平稳，最接近理想曲线。而当线圈匝数小于212时，电磁力过小而无法驱使动铁芯运动。

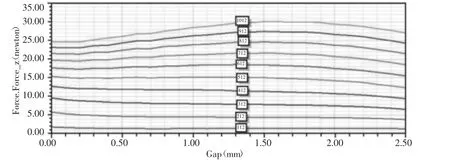
图5 不同线圈匝数下的电磁力特性曲线Fig.5 Electromagnetic Force Property Curve with Different Number of Turns

3.1.3 隔磁槽位置对电磁力特性的影响

线圈匝数不变、动铁芯厚度不变，仅变化隔磁槽位置，变化范围设置为以原位置向z轴负向平移3mm处为起点，再向正向平移6mm，步长为1mm。仿真得出不同隔磁槽位置的电磁力特性曲线，如图6所示。

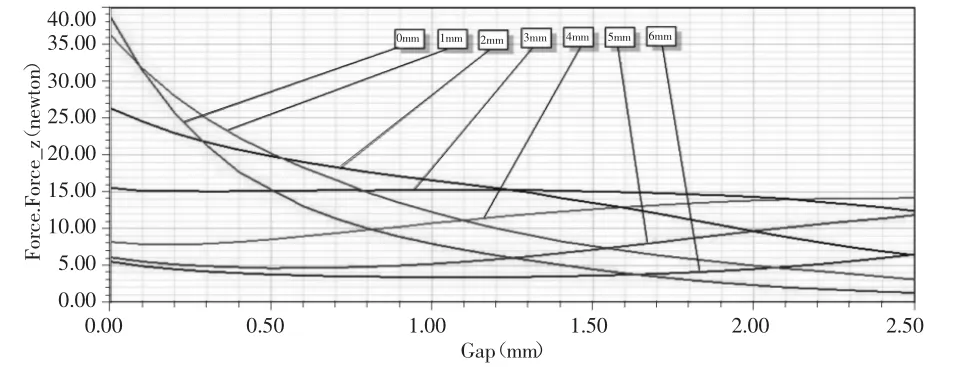
图6 不同隔磁槽位置的电磁力特性曲线Fig.6 Electromagnetic Force Property Curve with Different Positions of Isolation Groove

3.1.4 动铁芯厚度对电磁力特性的影响

线圈匝数、隔磁槽位置不变，仅变化动铁芯厚度，变化范围为［2.65，3.65］，步长为0.1（单位：mm）。仿真得出不同动铁芯厚度下的电磁力特性曲线，如图7所示。随着动铁芯厚度的增加，电磁力特性曲线的工作行程区由下垂到平稳再到上翘，其中厚度为［2.55，3.05］的范围内最平稳，最接近理想曲线。Band模型，如图8所示。

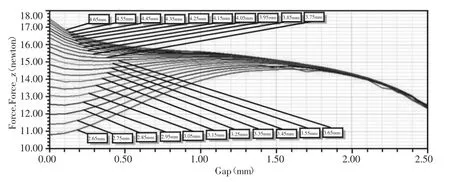
图7 不同动铁芯厚度下的电磁力特性曲线Fig.7 Electromagnetic Force Property Curve with Different Thicknesses of Core

3.2 动态磁场仿真分析

3.2.1 有限元建模

式中：U—驱动电压；i—线圈电流；R—线圈电阻；φ—通过动铁芯的磁通量总和。

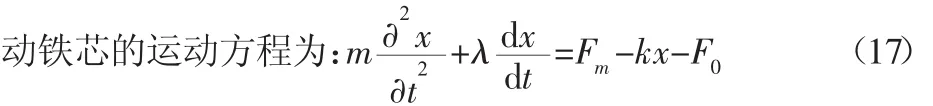
式中：m—动铁芯质量；λ—阻尼系数；x—动铁芯位移；k—弹簧刚度；F0—弹簧预紧力。

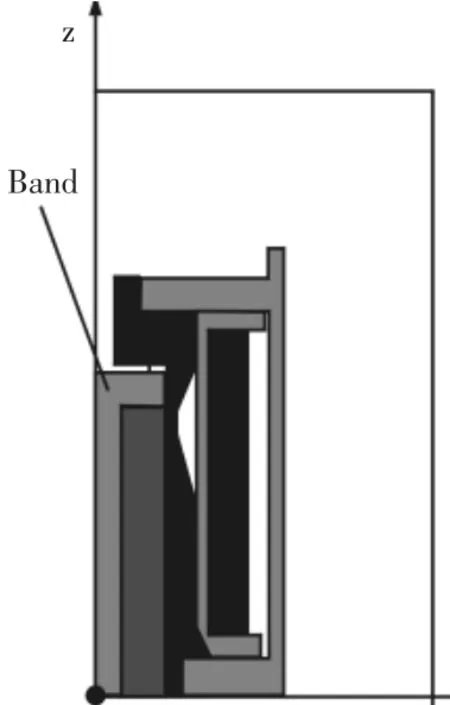
图8 Band模型Fig.8 Model of Band

3.2.2 线圈匝数对电流特性的影响

仿真得到不同线圈匝数下的电流特性曲线，如图9所示。在线圈匝数逐渐增大的过程中，电磁阀的触动点t0的时刻逐渐增大，而开启点t1呈先减小后增大的趋势且在212匝时最小。但是，当线圈匝数过小时，可能会因产生的电磁力过小，动铁芯无法运动至与静铁芯吸合。

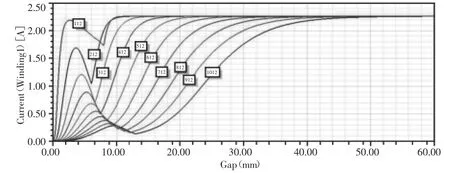
图9 不同线圈匝数下的电流特性曲线Fig.9 Current Property Curve with Different Number of Turns

3.2.3 隔磁槽位置对电流特性的影响

不同隔磁槽位置时的电流特性曲线仿真结果，如图11所示。从图中可以看到，隔磁槽平移距离由0mm增至6mm的过程中，t0和t1先减小后增大，在3mm处最小，即动铁芯开始运动的时间和电磁阀的开启时间最短。

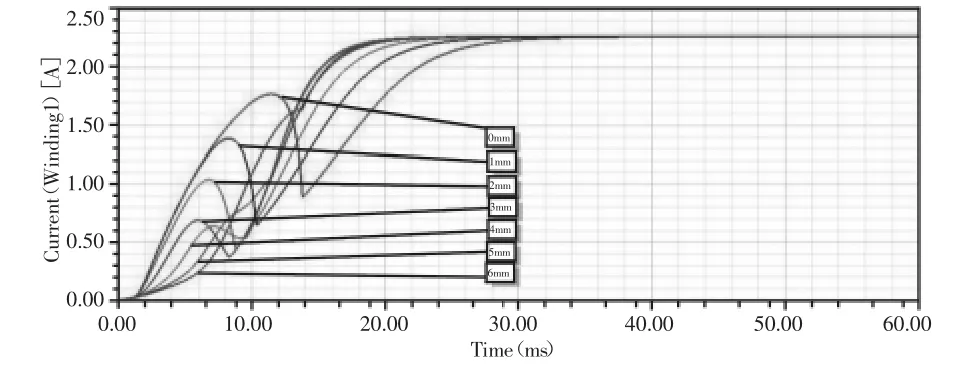
图10 不同隔磁槽位置的电流特性曲线Fig.10 Current Property Curve with Different Positions of Isolation Groove

3.2.4 动铁芯厚度对电流特性的影响

不同动铁芯厚度下的电流特性曲线仿真结果，如图11所示。由图11可知，虽然各电流特性曲线在t1时刻后的增长速率有略微不同，但是触动点t0和开启点t1的时刻基本相同。也就是说，动铁芯厚度不是电磁阀的开启时间主要影响因素。

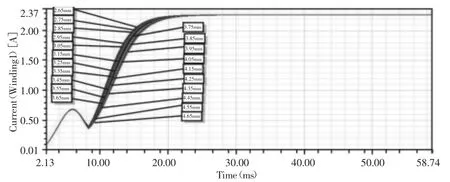
图11 不同动铁芯厚度下的电流特性曲线Fig.11 Current Property Curve with Different Thicknesses of Core

4 总结

（a）线圈匝数在［212，615］的区间内，电磁力特性曲线最平稳，最接近理想曲线，换挡精度最高。随着线圈匝数的增大，由电流特性曲线反映的电磁阀开启时间先减小后增大，在匝数为212时最小。由于在仿真时忽略了铁芯所受的阻尼力，因此在实际中匝数应稍微选大些。（b）隔磁槽位置由z轴负向向正向平移的过程中，电磁力特性曲线的工作行程区呈下垂-平稳-上翘的变化趋势，在3mm处最平稳，换挡精度最高。电流特性曲线所反映的电磁阀开启时间呈先减小后增大的变化趋势，在3mm处最小。（c）随着动铁芯厚度的增加，电磁力特性曲线的工作行程区由下垂到平稳再到上翘，其中厚度为［2.55，3.05］的范围内最平稳，换挡精度最高，考虑到材料成本，厚度可以尽量选小值。而动铁芯厚度对电磁阀开启时间的影响不大。

［1］刘林林.自动变速箱换挡电磁阀检测系统的设计与实现［D］.武汉理工大学，2012.（Liu Lin-lin.Design and Implementation of Testing System for Automatic Transmission Shif Solenoid Valve［D］.Wuhan University of Technology，2012.）

［2］柯明纯，赵建斌，闫念华.一种新型直动式比例电磁铁静态特性研究［J］.机电设备，2008，25（5）：14-17.（Ke Ming-chun，Zhao Jian-bin，Yan Nian-hua.Study on Static CharacteristicofaNewTypeofDirectlyProportional Solenoid［J］.Mechanical and Electrical Equipment，2008，25（5）：14-17.）

［3］胡燕平，张瀚.隔磁环参数对直流电磁铁电磁吸力影响研究［J］.液压与气动，2016（6）：46-49.（Hu Yan-ping，Zhang Han.Study on the Magnetic Force of the Solenoid about Isolating Ring’s Parameter［J］.Chinese Hydraulics&Pneumatics，2016（6）：46-49.）

［4］张榛.电磁阀动态响应特性的有限元仿真与优化设计［J］.空间控制技术与应用，2008（5）：53-56.（Zhang Zhen.FEA Simulation of Dynamic Response of Solenoid Valve and Its Optimal Design［J］.Aerospace Control and Application，2008（5）：53-56.）

［5］吴萌，熊庆辉，王浚哲.电磁阀开启过程动态响应特性有限元仿真研究［J］.长春理工大学学报：自然科学版，2015（2）：117-120.（Wu Meng，Xiong Qing-hui，Wang Jun-zhe.Finite Element Simulation Research on the Dynamic Response Characteristics in the Opening Process of Solenoid Valve［J］.Journal of Changchun University of Science and Technology：（Natural Science Edition，2015（2）：117-120.）

［6］范立云，刘鹏，马修真.柴油机电控单体泵高速电磁阀动态响应特性的影响因素分析［J］.内燃机工程，2014，35（4）：114-118.（Fan Li-yun，Liu Peng，Ma Xiu-zhen.Analysis on Factors Influencing Dynamic Response Characteristics of High-Speed Solenoid Valve for Diesel Engine Electron-Controlled Unit Pump［J］.Chinese Internal Combustion Engine Engineering，2014，35（4）：114-118.）

［7］谢英俊，娄相芽，金波.电液可变气门高速开关阀用电磁铁设计与研究［J］.工程设计学报，2010，17（2）：138-145.（Xie Ying-jun，Lou Xiang-ya，Jin Bo.Design and Study on High-Speed on/off Valve in Electro-Hydraulic Variable Valve System［J］.Journal of Engineering Design，2010，17（2）：138-145.）

［8］李泉凤.电磁场数值计算与电磁铁设计［M］.北京：清华大学出版社，2002．（Li Feng-quan.Numerical Calculation of Electromagnetic Fields and Design of Electromagnets［M］.Beijing：Tsinghua University Press，2002.）

［9］王泽忠，全玉生，卢斌先.工程电磁场［M］.北京：清华大学出版社，2011.（Wang Ze-zhong，Quan Yu-sheng，Lu Bin-xian.Engineering Electromagnetic Fields［M］.Beijing：Qinghua University Press，2011.）

［10］巩宪锋，马颖丹.井下涡轮发电机磁力传动机构的耦合磁场分析［J］.机械设计与制造，2014（2）：59-62.（Gong Xian-feng，Ma Ying-dan.Analysis of the Coupling Magnetic Field of the Magnetic Transmission Mechanism with Downhole Turbine Generator［J］.Machinery Design and Manufacture，2014（2）：59-62.）

［11］谢德馨，杨仕友.工程电磁场数值分析与综合［M］.北京：机械工业出版社，2008.（Xie De-xin，Yang Shi-you.Numerical analysis and synthesis of EngineeringElectromagneticFields［M］.Beijing：ChinaMachinePress，2008.）

［12］刘国强，赵凌志，蒋继娅.Ansoft工程电磁场有限元分析［M］.北京：电子工业出版社，2005.（Liu Guo-qiang，Zhao Ling-zhi，Jiang Ji-ya.Ansoft-based finite element analysis of engineering electromagnetic field［M］.Beijing：Electronics Industry Press，2005.）

［13］张功晖，黎志航，周志鸿.基于Maxwell方程的电磁阀开启过程动态特性仿真研究［J］.液压气动与密封，2010（11）：22-25.（Zhang Gong-hui，Li Zhi-hang，Zhou Zhi-hong.Simulation Research of Dynamic Character of Solenoid Valve’s Opening Process Based on Maxwell Equation［M］.Hydraulics Pneumatics&Seals，2010（11）：22-25.）