核极化的多核LSSVM及其在分类中的应用

刘文婧，陈肖洁

（内蒙古科技大学 机械工程学院，内蒙古 包头 014010）

1 引言

支持向量机（support vector machine，SVM）[1]是基于结构风险最小化，以统计学习理论为基础。SVM善于处理小样本、高维和非线性等问题。然而，SVM的最优分类超平面参数的获取是通过求解计算量复杂的二次规划，为减小SVM的计算花销，文献[2]提出了最小二乘支持向量机（leastsquaressupportvectormachine，LSSVM）。LSSVM的优势是求解一组线性方程组来得到最优分类面参数，极大地减少了计算复杂度。近年来，为增强决策函数的可理解性和可解释性，以便获取更优的泛化性能，多核学习（multiple kernel learning，MKL）[3]吸引了广大研究者们的眼眸。多核学习，顾名思义，就是多个基本核函数依据某种规则组合成新的核函数进行学习。在MKL框架下，通常需要考虑的问题是如何确定多个基本核函数的权系数（组合系数）问题。目前，关于多核权系数的求解问题，依分类器为划分标准，有如下两种方法：

（1）以SVM为分类器的MKL模型，多核权系数的求解方法有：采用核排列思想[4]和核极化思想[5]，即利用核排列或核极化确定每个基本核函数的权系数，无须反复训练SVM分类器，计算高效；文献[6]提出的局部多核学习，文献[7]提出的SimpleMKL算法，权系数的优化需要多次训练SVM分类器，计算量较大；

（2）以LSSVM为分类器的MKL模型[8-9]，循环迭代LSSVM分类器进行权系数优化。为了最小化计算开销，我们采用方法（1）中独立于分类器的核极化来确定多核的权系数和选用方法（2）的LSSVM为分类器。因此，将LSSVM、多核学习与核极化结合起来考虑，解决了盲目地选择核函数的问题，提出一种基于核极化的多核LSSVM算法模型，并将该算法模型应用于二分类和多分类中以观察所提出算法的有效性。

2 最小二乘支持向量机

二分类时，给定一组样本个数为L的训练集｛xk，yk｝∈Rn×｛+1，-1｝，在非线性分类的情形下，通过核函数的隐式定义 k（xi，yj）=（φ（xi），φ（yj）），φ（xi）：Rn→Rs，将样本数据从输入 n 维空间映射到更高维的S空间，目的是在高维的S空间中以线性的方式解决输入n空间的非线性分类问题。综合考虑函数复杂度和分类允许误差，二分类问题的数学语言可表述如下：

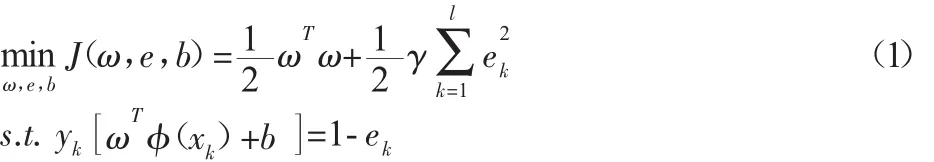
式中：γ—正则化参数；ei—松弛变量；b—偏置量。

构建Lagrange方程求解式（1）：

L（ω，e，b，α）=J（ω，e，b）-

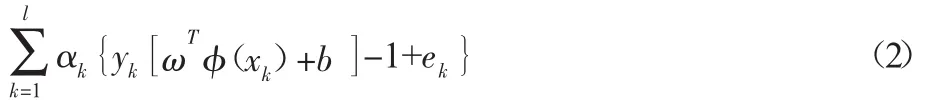
式（2），由 Karush-Kuhn-Tucker（KKT）条件可得：

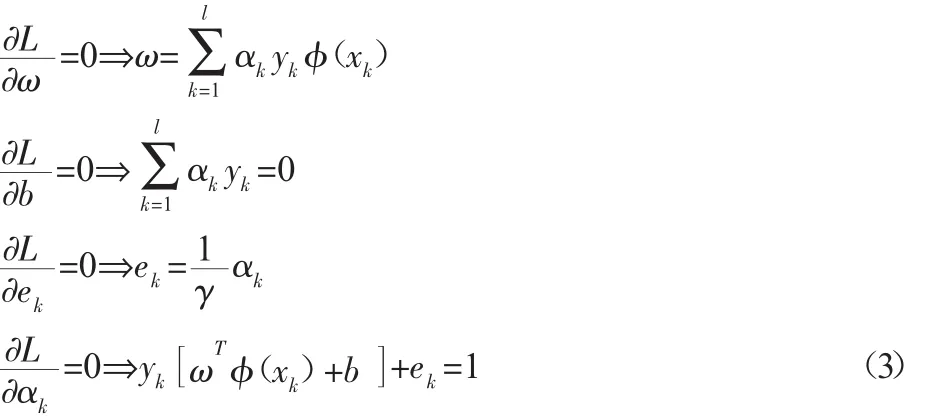
整理式（3），可得一组线性方程组，如下所示：

式中：Y=（y1，…，yl）T；Ωij=yiyjk（xi，xj）；I—与 Ω 同阶的单位矩阵；I1=（1，…，1）T的全 1 列矩阵，与 Ω 同行；拉格朗日乘子Y=（α1，…，αl）T。

通过解方程式（4），解得b和α，对未来输入样本x，LSSVM的输出决策函数为：

多分类时，目前，在实际应用中，多分类问题的求解方法主要有两种，一种为一次性多目标优化方法，另一种为将多分类问题转化为二分类问题。所谓一次性多目标优化，就是将所有的优化参数在一次的运算中均获得最优解，在求解过程中，由于变量数目多导致运算复杂，且最终的预测精度也不尽如意。第二种方法便于理解和实现，因此，我们将多分类问题转化为多个二分类问题进行多分类的求解，具体转化方式有一对多和一对一，前者易造成样本数据的失衡，为了使样本数据保持平衡，选用一对一方式。

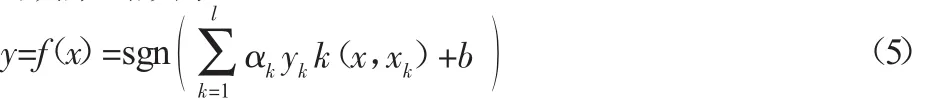
3 多核最小二乘支持向量机

多核最小二乘支持向量机（least squares support vector machinewithmultiplekernels，MK_LSSVM）算法的核心理念就是将M个类型不同的或类型相同参数不同的基本核函数k1，…，km进行线性的或非线性的加权组合，构造新的核函数，并用于LSSVM分类器的学习和预测。根据多核学习MKL[3，9]的原理，MK_LSSVM的决策函数为：

式中：μi—第i个基本核函数的权系数；M—基本核函数的总个数。

基于结构风险最小化原则，MK_LSSVM的原始优化问题表述为：

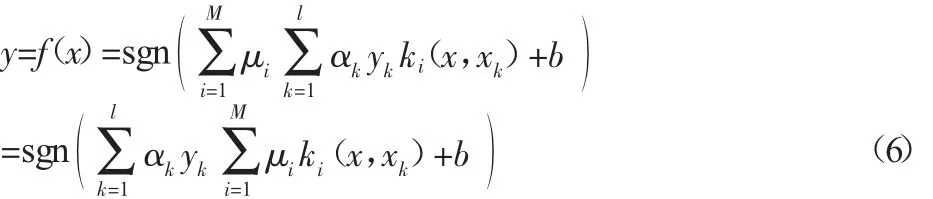
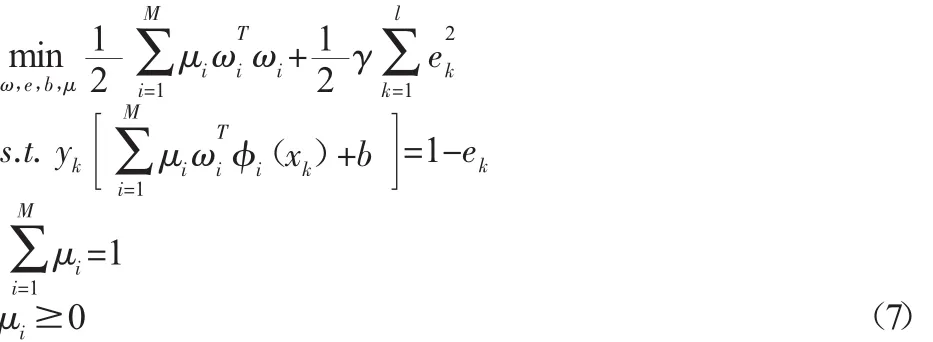
式（7），构建拉格朗日函数进行求解：

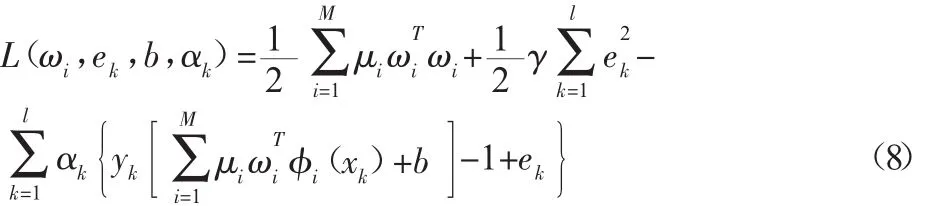
由KKT条件，分别对式（8）的各参数ωi，ek，b，αk求偏导，可得：

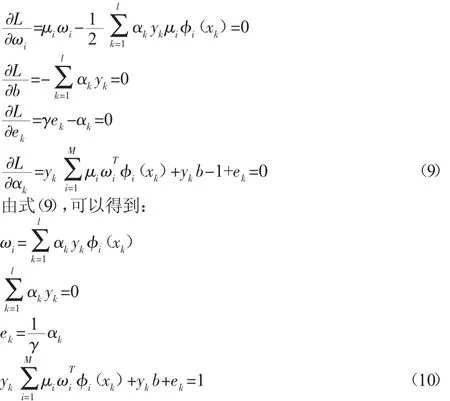
将式（10）整理为矩阵的形式如下：

Ωij=y—第 k 个核函数的权系数，其 μi值的确定，我们采用独立于分类器算法的核度量标准—核极化。

4 核极化的MK_LSSVM

4.1 核极化

2005 年，文献[10]提出了核极化（kernel polarization，KP）的概念，并给出了其定义式为：

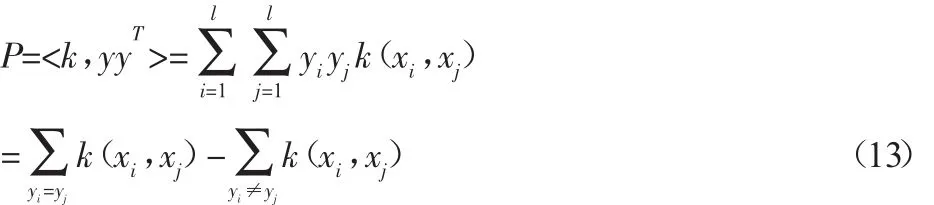
式中：k—核矩阵；

yyT—理想核矩阵。

Baram指出P的几何意义为当同类样本点相互靠近，异类样本点相互远离时，P值越大。在MKL框架下，可以这样理解，当某一核函数对样本正确分类的贡献率越大时，该核函数相对应的P值越大。因此，我们可以利用每一基本核函数的核极化值的大小来确定其权系数的大小，即

4.2 核函数

目前，使用广泛的基本核函数有：高斯核、多项式核、线性核等。我们选用全局性核函数—多项式核和局部性核函数—高斯核作为多核组合的基本核函数，高斯核和多项式核的表达式为：

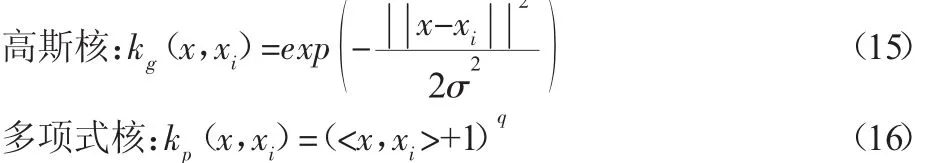
为了减小不同核函数之间的差异性，我们对核函数进行球形标准化处理，具体公式为：

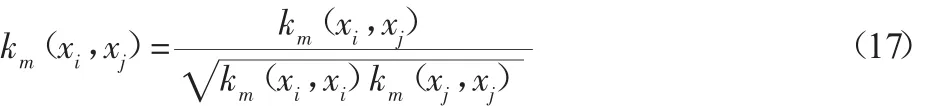
4.3 核极化的MK_LSSVM算法步骤

Step 1：二分类时，样本类别为｛+1，-1｝；多分类时，按一对一方式，将多分类转化为多个二分类；Step 2：选择基本核函数：高斯核和多项式核，并设置相应的核参数值σ和q；Step 3：基本核函数的标准化处理（见式（17））；Step 4：计算每个基本核函数的核极化值Pi，并按式（14）确定核函数的权系数μi；Step5：建立MK_LSSVM分类器算法模型，由式（12）确定a和b；Step 6：MK_LSSVM模型预测，根据式（6）预测新输入的样本x的类别。

5 实例仿真

为了验证所提的基于核极化的MK_LSSVM算法模型的有效性，我们从UCI标准数据库中选取6组数据集，分别为Breast、Heart、Banknote、Wine、Iris和 Glass，前三个为二分类数据集，后三个为多分类数据集，数据集的基本属性，如表1所示。

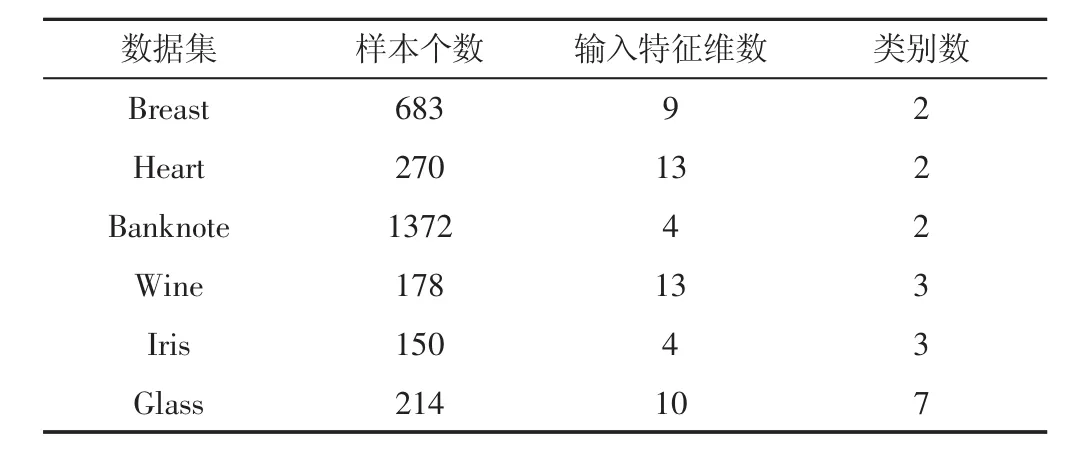
表1 试验的数据集简介Tab.1 The Data Set of Experiments

Breast为二分类，包含良性（Benign）和恶性（Malignant）两类，数据集的全称为WisconsinBreastCancerDatabase。Breast数据原有样本699个，因缺失16个样本数据，故实验中采用的样本为683个，每个样本含有9个输入特征Heart数据集二分类，包含270个样本，每个样本含有13个特征分量，具体特征属性为：年龄、性别、胸部疼痛类型、静息血压值、血清类固醇、空腹血糖值、静息心电图、最大心率值、运动性心绞痛、抑郁症、运动斜率、血管数和病患类型。Banknote为钞票数据集，二元分类问题（0为真钞，1为假钞），共含有的观察值1372个，4个连续的输入特征变量，分别为：小波变换图像、小波偏斜变换图像、小波峰度变换图像和图像熵。BanknoteDataset是依据给定钞票的特征预测是钞票的真假。Iris是IrisPlantsDatabase的简称，包含150个样本观察值，每个样本含有4个属性特征：萼片长度、花瓣长度、萼片宽度、花瓣宽度。3 类 setosa、versicolor、virginica，每个类的观察值均等，均为50个样本。WineRecognitionData数据集，多分类。Wine数据完整，无缺失，大小为178×13：样本数为178个，每个样本的输入特征为13个。数据来源自意大利同一地区三类不同品种酒的大量研究和分析。在数据“wine.data”中，178行，行代表酒的样本，其中，第1类：59个样本，第2类：71个样本，第3类：48个样本，即共有178个样本；14列，第一列：类标志属性，标记为“1”，“2”，“3”等三类；第2列至第14列为样本输入特征值。

试验前，所有样本数据集均经过平均值为0，方差为1的数据预处理，即

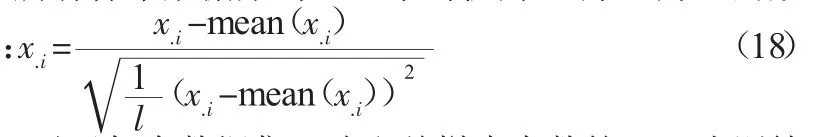
试验时，对于每个数据集，选取总样本个数的50%为训练集，剩余样本为测试集。按照第四部分的4.3的算法步骤，选取高斯核和多项式核作为组合多核的基本核函数，核参数分别取σ＝2、σ＝3 和 q＝2、q＝3。为证明所提算法的正确性，具体的 MK_LSSVM算法形式有：（1）高斯核（σ＝2）和多项式核（q＝3）组合的多核，简记为 MK_LSSVM_g2+p3；（2）高斯核（σ＝2）、多项式核（q＝3）和多项式核（q＝2）组合的多核，简记为 MK_LSSVM_g2+p3+p2；（3）高斯核（σ＝2）、多项式核（q＝2）和高斯核（σ＝3）组合的多核，简记为MK_LSSVM_g2+p3+g3。

采用的对比试验方法有：

（1）经典的5-折交叉验证的SVM，用台湾大学林智仁编写的工具箱Libsvm实现，选用高斯核，并C和高斯参数范围均为，［2-5，25］迭代步长为；（2）LSSVM 模型，选用高斯核，其核参数，记为LSSVM_g2；（3）基于核排列的多核SVM算法，选用高斯核（σ＝2）和多项式核（q＝3），即 MK_AlignmentSVM_g2+p3；（4）局部多核学习的SVM算法，即MK_LocalizedSVM_g2+p3；（5）广义化的多核 SVM 算法，即 MK_GeneralizedSVM_g2+p3；（6）GroupLasso多核SVM算法，即 MK_GroupLassoSVM_g2+p3；（7）Simple多核 SVM算法，即MK_SimpleSVM_g2+p3；（8）核极化的多核SVM算法，即MK_PolarizationSVM_g2+p3。

为了体现实验算法的客观性，选用分类准确率为算法评价指标，其中，为分类正确的样本个数，为总预测的样本个数。为了体现算法中公正性，我们采用10次独立试验的平均值。所有算法的试验结果，如表2所示。

表2中的粗体数值表示在该试验参数下最好的结果值，观察表2的试验结果，我们可以知道，就分类准确率而言，数据集Breast和Glass分别在算法MK_LSSVM_g2+p3和MK_LSSVM_g2+p3+p2上取得了最优的结果；数据集Banknote和Iris同样在所提出的MK_LSSVM算法上取得最优的分类准确率；在Heart和Wine数据集上，传统经典的5折SVM得到了最好的分类结果，所提出的MK_LSSVM的结果仅次于SVM。综上所述，试验结果说明了所提出的基于核极化的多核最小二乘算法是有效性。

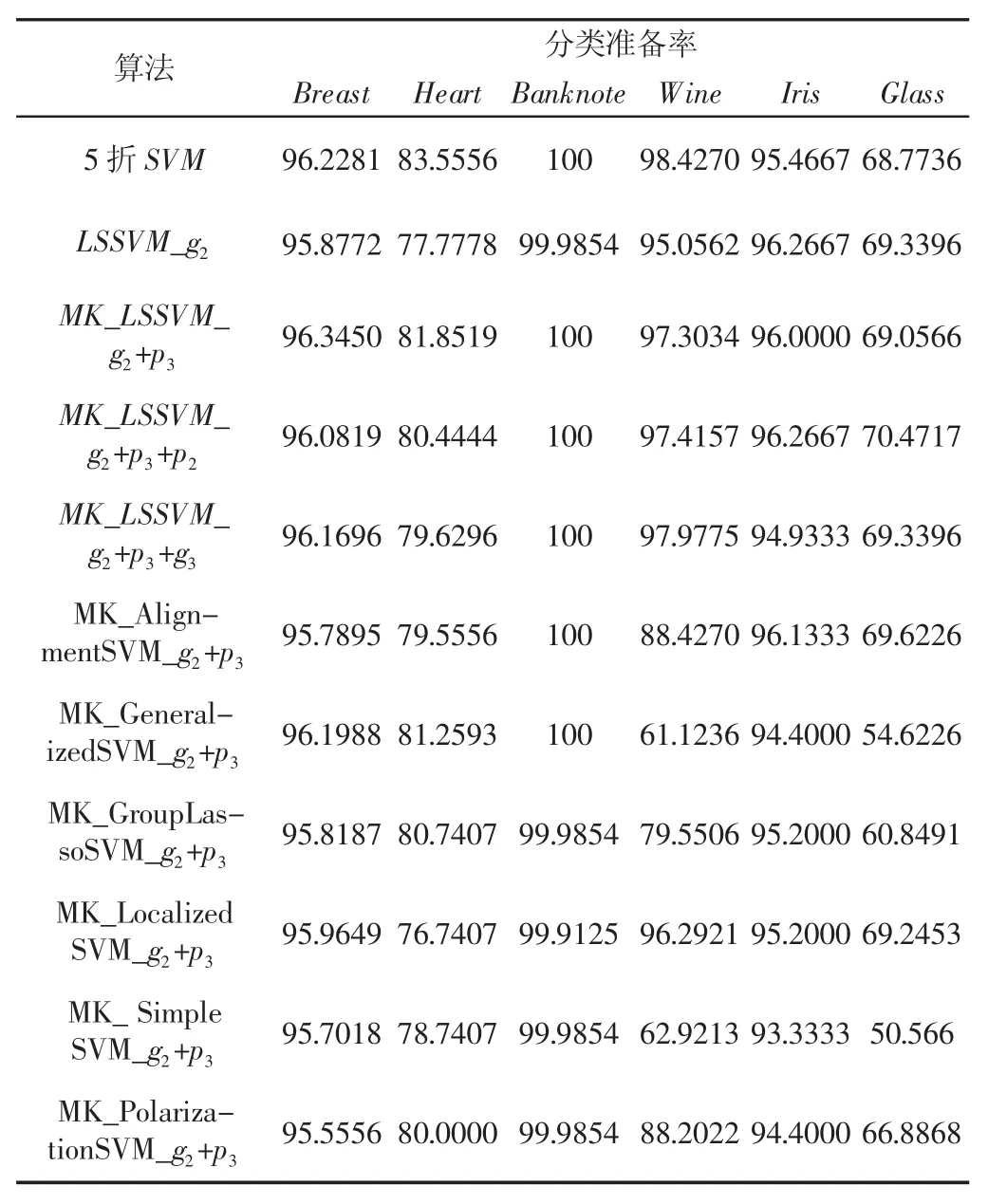
表2 试验结果Tab.2 The Results of Experiments

6 结语

在多核学习原理的指导下，引入了核极化，提出了基于核极化的多核最小二乘支持向量机算法模型，解决了LSSVM核函数选择盲目性的问题。UCI数据集上的试验结果表明MK_LSSVM算法的有效性。

［1］Vapnik V N.The Nature of Statistical Learning Theory［M］.New York：Springer Verlag，1995.

［2］Suykens J A K，Vandewalle J.Least squares support vector machines classifiers［J］.Neural Processing Letters，1999，9（3）：293-300.

［3］Mehmet Gonen，Ethem Alpaydin.Multiple kernel learning algorithms［J］.Journal of Machine Learning Research，2011（12）：2211-2268.

［4］He Junfeng，Chang Shih-Fu，Xie Lexing.Fast kernel learning for spatial pyramid matching［C］.In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition，2008.

［5］Wang Tinghua，Zhao Dongyan，Feng Yansong.Two-stage multiple kernel learning with multiclass kernel polarization［J］.Knowledge-Based Systems，2013，48（2）：10-16.

［6］Mehmet Gonen，Ethem Alpaydin.Localized multiple kernel learning［C］.In Proceedings of the 25th International Conference on Machine Learning，2008.

［7］Rakotomamonjy A，Bach F R，Canu S.SimpleMKL［J］.Journal of Machine Learning Research，2008（9）：2491-2521.

［8］Jian L，Xia Z，Liang X.Design of a multiple kernel learning algorithm for LS-SVM by convex programming［J］.Neural Networks，2011，24（5）：476-483.

［9］Chen X，Guo N，Ma Y.More efficient sparse multi-kernel based least square support vector machine［C］.Communications and Information Processing，Berlin：Springer-Heidelberg，2012：70-78.

［10］Baram Y.Learnning by kernel polarization［J］.Neural Computation，2005，17（6）：1264-1275.