基于节点属性的重叠社区发现算法改进*
王梦迪,付顺顺
(中国人民公安大学 信息技术与网络安全学院,北京 100038)
0 引 言
随着复杂系统科学和信息技术的不断发展,人们发现了越来越多的复杂网络。这些网络中,通常以节点表示个体,边表示个体间关系[1]。大量研究表明,在复杂网络中存在着一定的社区结构,它们具有相似的功能或属性,如社会网络中的家庭﹑朋友,蛋白质网络中的相似功能团等。社区发现的目标就是从无标记的网络中发现这样的节点组合。目前,在信息网络中,发现其中的社区结构,对用户进行正确的舆论引导,营造健康的网络环境,维护国家安全稳定[2];在犯罪嫌疑人的信息网络中,通过社区发现可以发现隐藏犯罪份子以及团伙的组织架构,给破案提供助益[3];在商业方面,社区发现可用于个性化商品推荐[4]。早期网络社区的研究主要基于“弱连接优势理论”,使得研究人员认为网络中的集群是由一些“信息虚线”连接而成,从而提出以图分割﹑模块度和中介中心性为基础的模型,即通过移除能使节点集间相互隔离的边来划分社区[5-7]。上述模型的基础是每个节点只能属于一个社区。但真实的社区之间存在一定程度的重叠,即一个节点可以属于多个社区。基于该思想,提出了派系过滤算法[8]﹑边聚类LC算法[9]﹑标签传播算法[10]和混合隶属度随机块模型[11]等。然而,大部分算法由于设定社区可重叠,可能使社区内部边比外部边少,从而导致非重叠区域的密度大于重叠区域这一不合理现象。
为了解决该问题,Jaewon通过改变以往社区发现算法中非重叠部分的链接密度高于重叠部分隐形假设,提出了社区隶属模型(Community-Affiliation Graph Model,AGM)[12]。通过该模型不仅能有效解决上述不合理现象,而且能准确识别重叠社区划分情况。然而,该算法主要存在以下两点不足。一方面,在MCMC采样阶段,判定采样结果是否能被接的过程中,仅考虑一个节点的隶属改变之后相关社区的概率似然值的改变程度,没有考虑该节点自身的节点属性对社区的隶属情况影响。另一方面,在计算社区似然值时运用的社区节点间生成边的概率仅考虑社区所提供的概率,没有引入节点间相似性对生成边的影响[13]。针对上述问题,本文在原有的MCMC采样过程中引入节点隶属影响,同时在计算节点间生成边概率时引入节点间相似性,以实现准确高效的社区识别。
1 基于社区隶属模型AGM的重叠社区发现算法
基于社区隶属模型AGM的社区发现算法是一种基于MCMC采样算法的社区发现算法,核心概念定义如下[12]。
定义1:首先假定影响节点之间建立连接的主要因素是节点所属的社区生成边的概率P,则节点u﹑v之间生成一条边的概率为:其中u﹑v属于节点集V,k∈Cuv表示节点u﹑v同时所属的社区。

定义2:基于定义1,当给定一个无向图G(V,E)时,则图G的似然函数为:
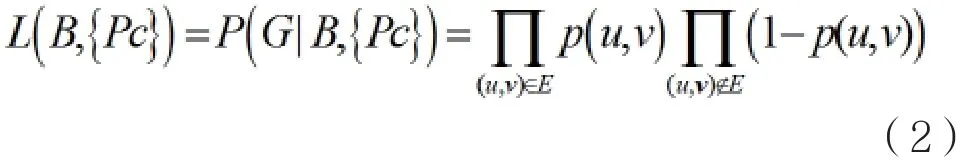
其中:B表示节点与社区之间关系的社区隶属图,常用形式为B(V,C,M)。如图1所示,V表示网络中所有节点的集合,C表示所有社区的集合,M表示社区与节点之间的关系集合。{Pc}表示社区内部节点之间生成边的概率。

图1 社区隶属关系
定义3:更新{Pc}时,保持社区隶属图B不变,则:

定义4:采用MCMC采样方法,对社区隶属图B(V,C,M)随机做出删除﹑增加和交换中的一种生成新图B'(V ',C ',M '),并以概率min(1,L(B',{Pc})/L(B,{Pc}))来决定是否接受该次变换。其中,删除表示随机的选择有隶属关系的节点u与社区C对(u,C)∈M,并将之从M中删除;增加表示随机选择无隶属关系的节点u与社区C对(u,C)∉M,将其增加到M中;交换表示随机的选择两个社区C1﹑C2和一个节点u,(u,C1)∈M,(u,C2)∉M,将(u,C1)从M中移除,(u,C2)添加到M中,如图2所示。

图2 MCMC过程
基于社区隶属模型AGM的社区发现算法的核心思想:首先给定复杂网络G(V,E),然后通过最优邻居节点法随机初始化社区隶属图B(V,C,M),最后采用MCMC方法对隶属图B(V,C,M)进行不断变换。当社区隶属图B对应的似然函数值最大时,得到的节点与社区之间的对应情况就是社区划分结果。
基于社区隶属模型AGM的社区发现算法进行实际应用时主要存在以下问题:MCMC采样阶段,判定采样结果是否能被接的过程中,仅考虑一个节点的隶属改变之后相关社区的概率似然值的改变程度,没有考虑该节点自身的节点属性对社区隶属情况的影响;在计算社区似然值时运用的社区节点间生成边的概率pc仅考虑社区所提供的概率,没有引入节点间相似性对生成边的影响。
2 基于改进MCMC方法的重叠社区发现算法
基于上述分析,提出了在原有的MCMC采样过程中引入节点隶属影响,同时在计算节点间生成边概率时引入节点间相似性,以实现准确高效的社区识别。
2.1 节点相似度构建
在复杂网络中,节点间相似性不仅与该节点的属性相关,还与该节点所处的局部网络环境相关。本文计算节点间相似度的方法是采用同邻居算法(Common Neighbors)。它是局部信息中最简单的相似性算法,表示的是若两个节点连接的相同节点数越多,则这两个节点相似程度越高。CN算法概念为:对于网络中的任一节点u,定义u的邻居节点集为φ(u),那么两个节点u和v的节点相似性Suv就定义为它们的共同邻居节点数量比上两个节点的全部邻节点数量[13],即:

相应地,式(1)改进为:

相应地,式(2)改进为:
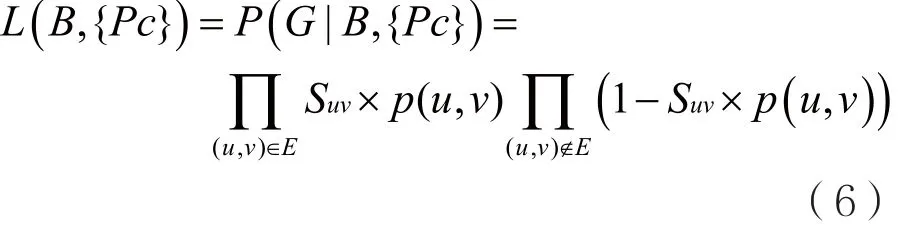
相应地,式(3)改进如下:
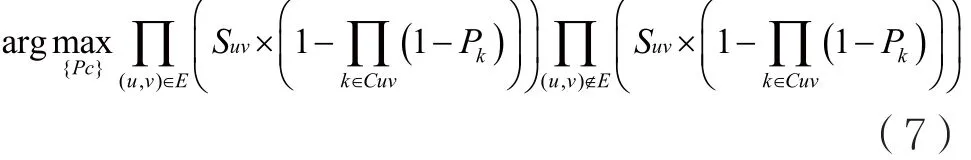
2.2 节点影响力构建
当某一节点的多个邻居节点属于该社区时,则可以认为该节点在社区的重要程度可能性越大,同时属于该社区的可能性越高。节点u与社区C之间的影响情况可表示为:

其中φ(u)表示u的邻居节点,C表示社区C包含的节点,|C|表示社区C包含的节点个数。
基于改进MCMC方法的重叠社区算法详细步骤如下:
输入:复杂网络G(V,E),最大迭代次数maxIter
For i=1 to maxIter do
使用STMCMC方法,在社区隶属图前一状态Bi中采样,获得新状态Bi+1

3 实验结果与分析
3.1 算法的评估指标
在基于AGM模型的社区发现算法中,用准确发现社区数U﹑平衡误差率BER和F1分数作为指标来评估算法[3,14]。假定算法发现的社区集为则准确发现社区数U﹑平衡误差率BER和F1分数的公式分别为:

3.2 实验数据
为了测试改进后的算法性能,利用斯坦福大学提供的四种真实世界网络数据[13]——amaon商品关系网络﹑DBLP科学合著网络﹑Youtube用户关注网络和LiveJournal社交网络进行社区发现实验。每种网络的数据规模如表1所示。
由于斯坦福提供的数据的社区结构已知,为了提高效率,从每个数据集中随机抽出50﹑100﹑150﹑200﹑300﹑500﹑1000个社区用做测试,抽取的数据包括社区成员节点以及与该社区成员相连接的其他节点。当然,为了保证这种实验方式的合理性﹑科学性,首先要求随机抽取,其次保证所抽节点集的节点度符合幂率分布,最后基于文献[15]可知,当社区个数达到1000时,各项实验指标会趋于稳定。具体地,所抽数据包含的节点个数及边数如表2所示。

表2 实验抽取数据
3.3 实验结果与分析
鉴于MCMC方法的随机性,最终选择结果为选取的每组数据进行50次运算后的平均值。
从图3﹑图4可以看出,算法在DBLP科学合著网络和Amaon商品关系网络中具有相似背景或者功用等,能导致社区节点之间联系紧密的网络社区划分效果较为优异。同时可以得出,在DBLP科学合著网络中,改进算法的性能比原算法提高约14%;在Amazon商品关系网络中,改进算法性能也提高的将近10%。从图6可以看出,算法在LiveJournal社交网络中也能做出有效的社区划分,并且算法改进后各项评估指标也较改进之前提高了9%左右。但是,从图5来看,改进前与改进后的算法在Youtube社区内部之间联系不太紧密的网络中,社区划分效果都不明显。综上所述,此类算法能很好地适用于社区节点之间联系紧密的网络中,且改进后的算法明显提高了社区发现的精确性和可靠性。
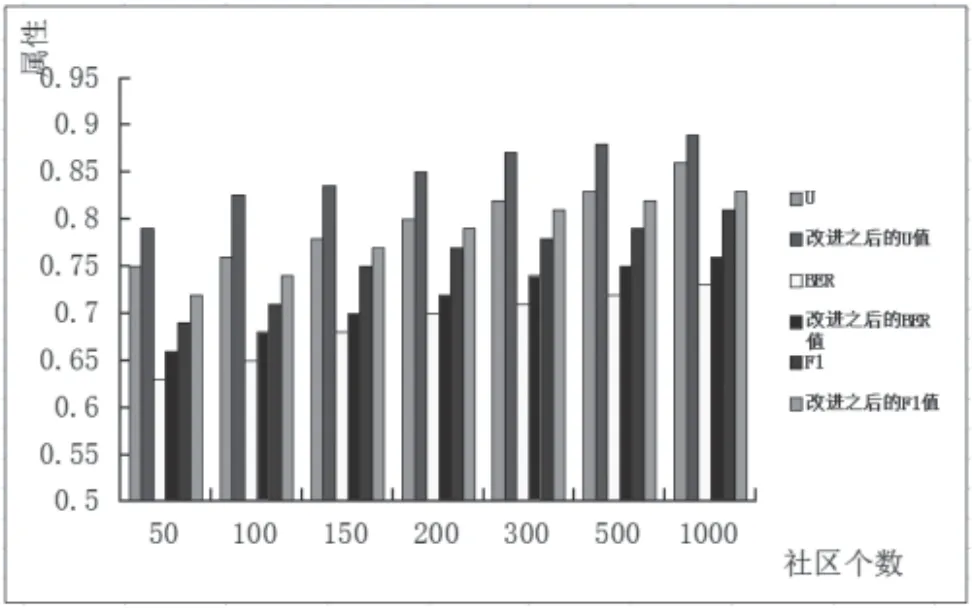
图3 在Amazon商品网络中的相关实验数据

图4 在DBLP科学合著网络中的相关实验数据

图5 在Youtube用户关注网络中的相关实验数据
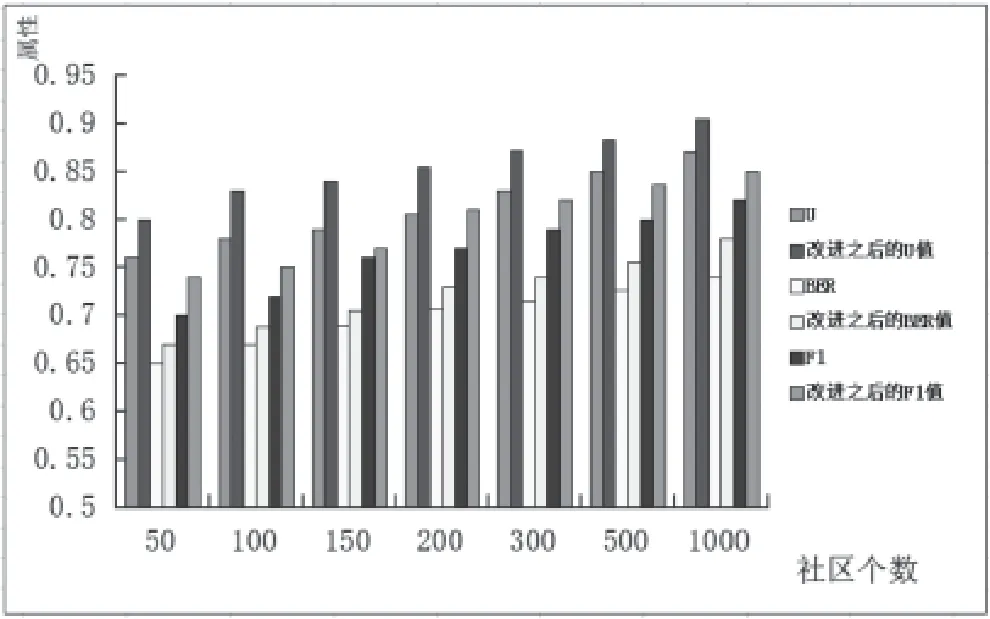
图6 在LiveJournal社交网络中的相关实验数据
4 结 语
本文分析基于AGM模型的社区发现算法的特点和不足,考虑节点相似性和影响力对生成边的影响,经过理论分析和在真实数据集上的测试可以得出结论,改进后的算法可以明显提高社区发现的精确性和可靠性。下一步,将更多考虑MCMC采样的优化方案,并考虑引入MapReduce﹑MPI等并行计算框架,以期实现算法的并行化。
[1] 程学旗,沈华伟.复杂网络的社区结构[J].复杂系统与复杂性科学,2011,8(01):57-70.
CHENG Xue-qi,SHEN Hua-wei.Community Structure in Complex Network[J].Science Technology of Complex Systems and Complexity,2011,8(01):57-70.
[2] 李玉翔.基于网络社区的用户兴趣建模与推荐技术研究[D].郑州:解放军信息工程大学,2013.
LI Yu-xiang.Research on User Interest Modeling and Recommendation Technology Based on Internet Community[D].Zhengzhou:PLA Information Engineering University,2013.
[3] 刘岩,顾益军,张大瀚.基于节点相似度的个人网络社交圈发现算法改进研究[J].网络安全技术与应用,2016(09):49-52.
LIU Yan,GU Yi-jun,ZHANG Da-han.Research on Improvement of Social Network Discovery Algorithm Based on Node Similarity[J].Network Security Technology and Application,2016(09):49-52.
[4] 陈晶,万云.社交网络中基于模块度最大化的标签传播算法的研究[J].通信学报,2017,38(02):25-33.
CHEN Jing,WAN Yun.Study on Tag Propagation Algorithm Based on Modularity Maximization in Social Networks[J].Journal of Communication,2017,38(02):25-33.
[5] Fortunato S.Community Detection in Graphs[J].Physics Reports,2010,486(03-05):75-174
[6] 顾益军,解易,张培晶.面向有组织犯罪分析的人际关系网络节点重要性评价研究[J].中国人民公安大学学报:自然科学版,2013(04):66-68.
GU Yi-jun,XIE Yi,ZHANG Pei-jing.Study on the Importance of Network Node of Human Relationship Network for Organized Crime Analysis[J].Journal of Chinese People's Public Security University: Natural Science Edition,2013(04):66-68.
[7] 顾益军,夏天.融合LDA与Text Rank的关键词抽取研究[J].现代图书情报技术,2014(07/08):41-47.
GU Yi-jun,XIA Tian.Keywords Extraction Using Fusion LDA and Text Rank[J].New Technology of Library and Information Service,2014(07/08):41-47.
[8] Gergely Palla,Imre Derényi,Illés Farkas,et al.Uncovering the Overlapping Community Structure of Complex Networks in Nature and Society[J].Nature,2005(435):814-818.
[9] Ahn Y Y,Bagrow J P,Lehmann S.Link Communities Reveal Multiscale Complexity in Networks[J].Nature,2010,466(7307):761.
[10] 张俊丽,常艳丽,师文.标签传播算法理论及其应用研究综述[J].计算机应用研究,2013,30(01):21-25.
ZHANG Jun-li,CHANG Yan-li,SHI Wen.A Review of Tag Propagation Algorithms and Their Applications[J].Application Research of Computers,2013,30(01):21-25.
[11] 柴变芳,贾彩燕,于剑.基于统计推理的社区发现模型综述[J].计算机科学,2012,39(08):1-7.
CHAI Bian-fang,JIA Cai-yan,YU Jian.A Survey of Community Discovery Models Based on Statistical Reasoning[J].Computer Science,2012,39(08):1-7.
[12] Yang J,Leskovec J.Community-Affiliation Graph Model for Overlapping Network Community Detection[C].IEEE International Conference on Data Mining,2012:1170-1175.
[13] 东昱晓,柯庆,吴斌.基于节点相似性的链接预测[J].计算机科学,2011,38(07):162-164.
DONG Yu-xiao,KE Qing,WU Bin.Link Prediction Based on Node Similarity[J].Computer Science,2011,38(07):162-164.
[14] Yang J,Leskovec J.Defining and Evaluating Network Communities Based on Ground-Truth[C].IEEE International Conference on Data Mining,Computer Society,2012:745-754.
[15] Yang J,Leskovec J.Overlapping Communities Explain Core-Periphery Organization of Networks[J].Proceedings of the IEEE,2014,102(12):1892-1902.

