基于超限学习机的通信网络弹性预测方法*

郑小禄，黄 宁，徐 侃

（北京航空航天大学 可靠性与系统工程学院，北京 100191）

0 引 言

网络容错策略能够使网络在遭受故障时，通过主动或被动的容错机制抵御故障，保证网络的可靠性[1-3]。为了保证系统的容错能力达到最佳，通常根据网络的分层特性，在不同层面上部署多个容错机制，形成混合容错策略来提升网络的容错能力，从而保证网络的可靠性[4]。对于网络容错能力的评价，目前主要通过对网络弹性的定性和定量评估来实现[5]。网络弹性定义为，网络在遭受攻击或失效后，网络可靠性恢复到正常状态的能力。因此，考虑容错策略的前提下，评估和预测网络的弹性，是网络设计阶段容错设计面临的重要问题。

为了评估和预测网络弹性，相关学者进行了大量研究，其中大部分研究集中在网络弹性评估方面。关于网络弹性的评估研究，主要是基于模型的弹性评估。根据S. Hosseini等学者[6]对网络弹性评估的方法分类，按照不同的容错机理，可以将弹性评估分为基于结构和拓扑的弹性评估和基于性能的弹性评估。其中，基于结构和拓扑的弹性评估主要通过对网络物理层拓扑具有的鲁棒性和容侵性进行建模，然后基于模型分析网络弹性。例如，A. Sydney等学者[7]基于复杂网络理论，提出了通过网络拓扑自然连通度来衡量网络结构的弹性；进一步地，M. J. F. Alenazi等学者[8]提出了利用网络“谱测度”来衡量网络结构弹性，同时证明谱测度优于其他连通性参数，更能表征网络结构所具有的弹性。基于网络性能的弹性评估研究主要是对网络运行状态参数如时延﹑丢包率等，根据状态空间法等方式进行建模，进而基于模型对网络弹性进行评估。D.Zhang等学者[9]在此基础上考虑移动因素对网络弹性的影响；J. P. Rohrer等学者[10]在考虑网络逻辑层协议的基础上，提出了网络弹性是物理层拓扑容错和逻辑层容错协议共同影响的结果。网络弹性的预测相对于网络弹性的评估，是网络弹性领域新兴的热点，主要思路仍然是基于网络运行参数和设计参数，通过对网络弹性进行建模，以这些参数和网络弹性水平之间的映射关系预测网络弹性[11-15]。目前，比较具有代表性的研究是J.Gao和Barabási A L[13]提出的基于“模式”的预测方法。该方法基于复杂网络理论，通过抽象出网络控制相关的结构参数和网络状态参数的映射，将网络多维动态模型抽象为一维模型，从而形成与弹性相关的模式，进而通过模式预测网络弹性。

综上所述，目前网络弹性预测研究大多是延续弹性评估的研究成果，利用模型驱动方法，以模式分类﹑状态空间方法等，基于已有的网络结构等设计参数预测网络弹性。然而，网络作为一种复杂的对象，呈现出动态性和耦合性特征。因而，在混合容错策略内部也存在这种耦合影响关系。现有的弹性预测方法仅仅能通过单一的容错策略进行预测，如在具有某种容错拓扑结构下，通过容错拓扑的结构参数来预测网络弹性，而基于逻辑层或基于多层混合容错策略的弹性预测，由于缺乏对逻辑层容错策略的定量分析和建模研究，导致当前的弹性预测方法不能支持考虑多种容错机制耦合下的弹性预测。对于网络弹性预测领域，由还原论思想导致的问题，本文从整体论思路出发，提出了一种基于数据驱动的﹑基于机器学习和弹性理论相结合的弹性预测方法。在对网络容错策略进行量化建模分析的基础上，利用机器学习方法在非线性系统模式识别和线性拟合领域所具有的优势[16]，采用超限学习机这一新兴的高效机器学习算法[17]预测网络弹性，不仅全面考虑了不同层面容错策略对整网弹性的影响，而且能够直观反映不同容错策略下网络的弹性变化趋势，为进一步研究混合容错策略耦合对系统可靠性的影响打下了理论基础。

1 网络容错策略模型构建

根据网络分层理论的定义，网络的应用和具有的功能是基于网络物理层和逻辑层的路由等传输协议实现的。路由协议作为规定网络上数据传输的路径准则，直接影响网络功能和应用的正常运行。而路由协议所产生的路由表，则是在下层物理层连通路径的基础上建立的。在宏观时间尺度上，网络的物理层以及由物理层之上路由协议等逻辑规则产生的逻辑层，各自在结构和空间维度上随着时间变化呈现出时空的动态性特征[14]。基于此，本文为了描述这种网络的时空动态特性，构建了网络时空动态模型。

1.1 网络时空动态模型

网络时空动态模型是为了描述网络逻辑层和物理层的时空动态特征，进而可以在此网络模型基础上对部署在这两个层面的混合网络容错策略进行建模。综上所述，网络时空动态模型由两部分组成：由物理连接构建的拓扑物理层和由路由等协议构建的逻辑层。

在此模型上，物理层的连通性变化有可能是由

该模型通过计算节点对(u,v)之间存在链路的概率来得到。其中，β、α∈(0,1]是模型调节参数，α表示长链路和短链路的比例，α越大，长链路越多；β表示链路的密度，β越大，链路密度越大。d(u,v)表示节点对(u,v)之间的欧氏距离，L是任意两个节点之间的最大欧式距离。

（2）逻辑层模型。同样，为了便于描述和定义逻辑层的时空动态特性，本文定义逻辑层如下：逻辑层可以被考虑成一个有向图G=(V,E )，其中V代表网络节点的集合，|V |代表网络节点的个数，对于u∈V，表征了一条节点u和v之间的有效物理路径，记为e；而(u,v)表示了u和v之间的逻辑连接，记为e(u,e)。E={e|u∈V,v∈V}为网络中逻辑层有效边的集合，有效边的个数记为|E|。定义一个函数W：E→R+,W(e)表示e的权值，记为w(u,v)。如果w(u,v)为+∞，说明e是断开的。集合V在这里定义为v1到vn的路径；对于，vk-1是vk所在路径上的下行节点；对于vi∈v,vj∈v,Path(vi,vj)表示源节点为vi﹑目的节点为vj的物理路径集合，vi∈v,vj∈v,path(vi,vj)为同样OD节点对逻辑连接的集合，f( path(vi,vj))表示对路径path(vi,vj)的评价函数。因此，对于从vi到vj的数据包的传输过程，这里建立有效传输的过程就是其寻找最优路path*(vi,vj)的过程，即为寻找评价函数最优化的过程，定义如下：于节点移动造成的，如MANET网络﹑移动蜂窝通信网络等具有移动特征的网络，节点具有强移动特征。因此，由于节点的移动特征和节点发射功率半径的约束，网络的物理拓扑呈现时空动态性。相应地，为了实现数据有效传输，路由协议会更新路由表，因此在逻辑层也呈现出时空动态性。此外，对于有线网络和无线网络，网络节点和链路的失效也是导致网络物理层和逻辑层呈现时空特征的原因。

为了构建网络动态模型，本文引入以下定义。

（1）物理层模型。基于网络物理层的时空动态性特征，可以借鉴已有的随机图模型来构建物理层网络模型。如Gilbert graphs﹑Waxman graphs和Gabriel graphs等模型[8]，通常被用来对无线网络的物理拓扑进行建模。这里为了更好地体现物理层容错策略的特征，选取Waxman模型[18]作为物理层网络模型：

满足于：

物理层可以通过waxman模型得到，逻辑层由相应的路由策略得到最优路径。由于节点失效或节点移动导致的物理层变化会对逻辑层路由选择造成影响，从而改变了逻辑层的节点连接情况。至此，能够反映网络时空特征的网络模型建立完毕，下一步可以在这个基础上开展网络容错策略建模的研究。

1.2 容错策略模型

对应于网络时空动态模型，网络的容错策略模型由两部分构成：物理层容错策略模型和逻辑层容错策略模型。

1.2.1 物理层容错策略模型

从网络科学的角度来看，网络结构或拓扑特征能够反映网络一些运行时的行为特性。前文中已经提到，复杂网络的相关研究证明，网络的拓扑特性可以决定网络的鲁棒性和生存性。因此，与这两种特性有紧密关系的网络弹性，也可以由网络结构相关参数来表征。这也是网络弹性评估方法中，基于网络结构和拓扑方法的依据[6]。通过文献调研，有很多网络鲁棒性相关的参数可以用来表征网络弹性，如前文提到的谱测度﹑自然连通度等。然而，这些参数都没有考虑对数据包传输的影响，仅仅是从连通性的角度对网络弹性做评价。例如，在相同的连通性下，高聚类系数网络中节点聚集密度更大，比低聚类系数网络的传输性能要好。基于这种情况，近年有学者提出了“流鲁棒性”的概念[10]，即以端对端连通节点数量作为对物理层弹性的测量。此外，有研究证明，该参数要优于自然连通度﹑谱测度等参数[19]。因此，对于物理层容错策略模型，本文结合“流鲁棒性”理论构建了物理层容错策略模型，并提出了物理层弹性参数phyFR：

其中，G=(n,l )表示有n个节点l条边的网络，{Componenti;1＜i＜k}为G中连通子团的节点个数。|n|是指网络中的节点数目。

1.2.2 逻辑层容错策略模型

逻辑层容错策略的实质是建立维护多条容错链路。当一条链路上的网络构件受到损坏时，能够快速切换到另外一条逻辑链路或尽可能快地重新发现并维护一条新的逻辑链路。基于这种思想，本文将这种逻辑容错策略特有的路径多样化特征抽象为逻辑层容错策略的模型，并提出相应的逻辑层弹性参数LFT：

其中，D(Pk)定义为路径多样化函数，源节点s，目的节点d，path P是连接两个节点的路由，记为P=L∪N，L和N分别是path所经过的链路和节点的集合。|P|表示path P所有节点（除起点和终点外）和链路个数的和。该多样化函数最早被用来分析美国通信主干网的传输层弹性[20]，基本思想是根据path（由物理层﹑数据链路层和网络层决定）的个数来衡量一对OD对之间传输的可靠度。这里举例说明逻辑层容错策略的计算方法，如图1所示。

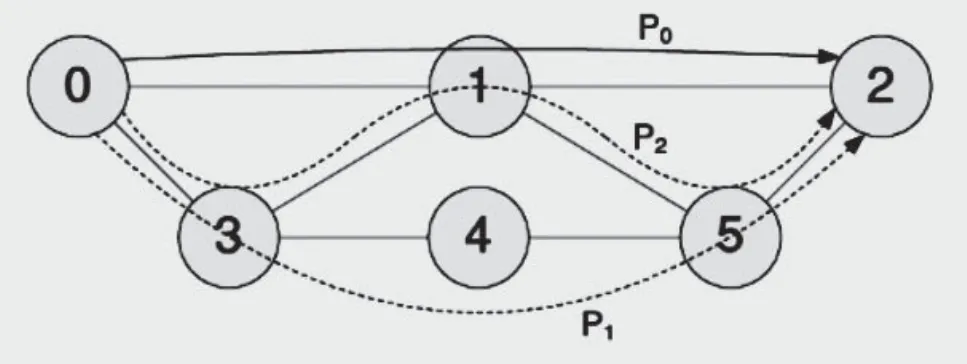
图1 某种基于多路径的逻辑层容错策略

图1是一种通过建立多条逻辑路径(P0,P1,P2)的逻辑容错策略，则此时计算过程简述如下：

在完成以上容错策略模型建模的基础上，需要根据模型定义，生成用于弹性预测的训练集和测试集数据。这部分工作依赖于对整网自下而上的仿真。相对于当前的内模型仿真算法，该模型在基于离散事件仿真器的网络仿真平台上的实现，主要体现在对协议栈层的抽象化二次开发。通过对路由协议进行参数化抽象，在容错机制层面上对多种协议进行仿真建模。然后，根据量化的容错策略模型收集需要的数据作为下一步预测算法的训练集和测试集。以目前通用的开源网络仿真平台NS3为例，数据生成和收集在NS3平台上的算法实现如图2所示。网络设计要素部分，配置文件是平台的输入部分，包含网络拓扑（邻接矩阵）﹑数据传输速率和数据加载速率。输入平台后，该部分在路由策略子模块基础上，实现实时对网络逻辑层空间特征参数的收集，遍历输入拓扑的所有接口，并遍历节点进而判断节点是否有路由功能，生成路由表。此外，根据逻辑容错策略模型的定义，对逻辑容错策略参数进行计算并输出，完成训练数据与测试数据的收集。

2 基于超限学习机的网络弹性预测模型

在完成网络容错策略模型的基础上，本文可以根据模型中定义的参数，从网络运行数据中提取相应的结构化数据，利用网络弹性预测模型对网络弹性进行预测。文献[13]提到，当前描述系统弹性的数学方法是用一个一维的非线性动力学方程去逼近复杂系统的行为：

其中，f(β, x)代表系统的弹性，参数β代表捕捉的环境变化条件。进一步地，一个由N个组件组成的网络，其节点状态集为x=(x1,…,xN)T，服从下述耦合非线性方程：

非线性函数F(xi)和G(xi,xj)代表了控制系统组件的动态规则，权值矩阵Aij反映了组件间的相互关系。适当选择函数F(xi)和G(xi,xj)，式（13）可以用来对很多系统进行建模，从而得到他们的弹性。而机器学习作为一种优秀的逼近方法，在弹性预测领域无疑是一种比较理想的选择。其中，f (aix+bi)可以从数据层面，结合激活函数和偏执，用来表征数据反映的系统动态规则。与式（13）中的F(xi)和G(xi,xj)作用相似，经过训练的输出权值矩阵β^可以用来表征Aij。

因此，关于网络弹性预测模型，本文利用超限学习机（ELM）构建网络弹性预测模型。超限学习机作为近些年来开始流行的机器学习方法，是一种前馈单隐层神经网络模型。相对于其他机器学习方法，它具有速度快﹑泛化能力强等优势[17]。因此，本文选取超限学习机作为预测模型的基础。

2.1 基于超限学习机预测模型的定义

图3为一个典型的超限学习机模型，(a,b)为隐藏节点的输入权重和偏置（阈值），训练样本集为(x,T )（对应于一组训练样本）。

其中，x表示训练样本的自变量，即可以对应于容错策略模型中各种能表征弹性的网络设计相关参数（phyFR和LFT等），以及和网络各类设计或配置参数，如拓扑结构﹑移动模式﹑流量模型等。t表示因变量，可以对应网络实际运行的水平，即对应于弹性值中能够代表网络运行能力的参数，如数据包传递成功率﹑丢包率﹑时延等。隐层映射函数（激活函数）表示为f(x)。这里，为了保证激活函数连续可微，选用sigmoid函数原因在下文中解释。输出权重表示为β，隐层的节点个数为L，oi表示为网络的学习误差，则该神经网络以损失函数表达为：

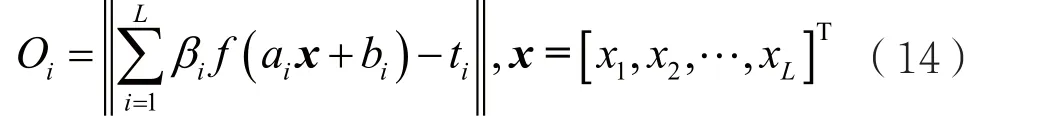
设隐层的输出矩阵为H，期望输出为T，则有：

因此，可得到：

其中：β=[β1,β2,…,βL]T，T=[t1,t2,…,tL]T。

图3 超限学习机模型结构

当学习误差为0时，即认为超限学习机具有了最好的学习能力。此时，Hβ=T，其中H为已知部分（输入权重，偏置，训练样本自变量），T亦为已知部分（训练样本因变量），则用超限学习机学习的过程就是根据Hβ=T得到β的过程。

然而，通常情况下，隐层节点数（随机得到的）要远小于训练样本数，此时矩阵为奇异矩阵不可逆。因此，该过程转化为求解输出权重β的最小二乘值

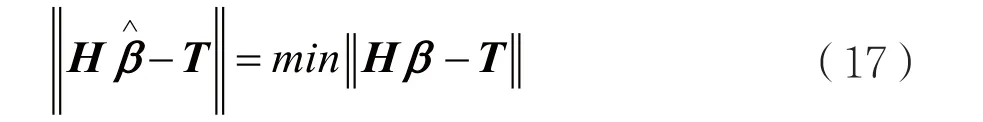
对应地，广义逆矩阵可用于求解奇异矩阵的逆矩阵。若H非奇异时，广义逆矩阵等价于H-1。若用H+表示H的广义逆矩阵，则β^的计算公式为若H+为H的Moore-Penrose广义逆矩阵，则可证得所得的解值最小且唯一。

训练中，输出权重β通过迭代不断优化，因此整个ELM网络的学习过程可以定义为：

需要注意的是，极限学习机相对于其他基于神经网络的机器学习算法，在效率上具有绝对优势。原因是：根据插值定理和普通极限定理[21]，当前馈神经网络（Single-Hidden Layer Feedforward Neural Network，SLFN）的隐层映射函数满足无限可微时，其学习能力与输入权重﹑阈值（偏置）等参数的选取没有相关性，仅仅跟当前的网络结构相关。因此，相对于其他方法，在激活函数选择为连续可微函数的前提下，超限学习机输入层权值a和偏置b可以从Rn和R空间的任何区间内，根据任意连续的概率分布随机生成，仅需要迭代训练输出层权值即可。

2.2 基于超限学习机的网络弹性预测算法

基于以上预测模型的定义，可以通过以下方法对网络弹性进行预测。

（1）在输入权重和阈值（偏置）的权值范围内随机为L个节点生成输入权重和阈值：(ai,bi),i=1,2,…,L，同时选定连续可微的函数作为激活函数。这里除了可以选择Sigmoid函数，还可以选择径向基函数（RBF）作为激活函数，从而使极限学习机在处理高维数据时避免过拟合现象。在本文的算法设计中，基于极限学习机理论对算法做了改良。在第一步初始化构建SLFN网络时，不仅可以指定隐层节点的个数，而且可以随机为隐层节点指定不同的激活函数，以此提高整个学习算法的泛化能力。

（2）实际应用中，可以选取隐藏层混合激活函数为：

其中：

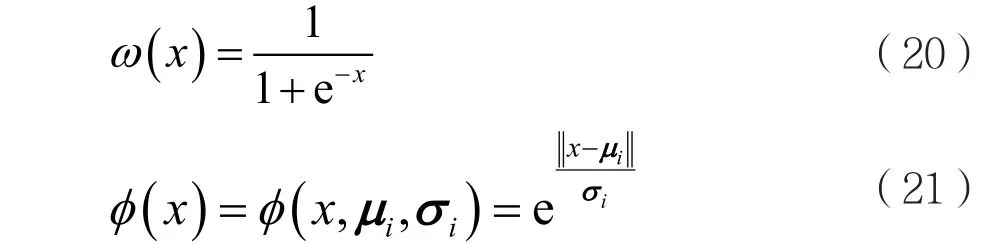
（3）根据式（22）计算隐层输出矩阵H：

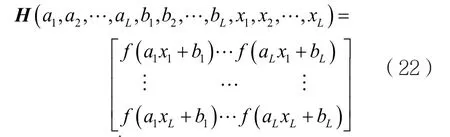
这样就可以将此过程简化为简单的线性变换过程。至此，基于超限学习机的预测模型和方法建立，本质是通过大量的训练样本训练模型，寻求β^的过程。一旦可以得到最优的β^值，就可以根据训练好的输出权值矩阵和激活函数，对任意输入的和网络设计的有关参数做网络弹性的预测。下面将通过一个简单的案例验证本方法的有效性。

3 案例验证及讨论

为了更好地体现网络的时空动态特性，研究在这种特性下网络容错策略对网络弹性的影响。这里以移动自组织网络（Mobile Ad hoc NETwork，MANET）为对象构建案例。

案例介绍：文献[10]设定了一个较为贴近现实使用剖面的案例用来对比各种弹性评价方法的优劣，因此本文的案例设定基于该文献的启发，设置如表1所示。

基于AODV路由算法和时空动态网络模型，在NS3仿真平台上对该案例进行实现，运行结果如图4﹑图5所示。

表1 仿真设置

图4 失效节点为0时逻辑层连通性

图5 失效节点为20时逻辑层连通性

仿真时，改变Waxman模型的α和β参数，随着网络失效节点增加，网络物理层的弹性变化如表2所示。

从表2可以看出，在相同逻辑层设定下，不同的物理层参数设置，网络呈现出不同的容错能力。因此，网络物理层参数和逻辑层容错参数之间存在线性或非线性关系，可以用机器学习的方法对这种关系进行数据驱动的启发式建模，从而达到预测的目的。然而，本文的目的是建立网络容错策略和网络弹性水平之间的映射关系模型，从而基于这个模型实现对网络弹性预测的目的。因此，进一步地，本文扩展了仿真实验的场景，增加网络的规模到1000个节点，并引入DSR协议作为和AODV协议的对比，全面讨论逻辑层和物理层容错策略参数和网络弹性水平的关系，结果如表3所示。

表2 仿真结果（phyFR）

表3 扩充的对比仿真实验设置

仿真仍然在NS3平台上实现并运行，在加入了DSR协议作为对比后，两种协议在逻辑层容错策略的能力如图6所示。

图6 AODV协议和DSR协议在不同失效节点比例下的容错能力（LFT）

图6纵坐标代表逻辑层的容错能力，横坐标代表有效节点的比例。其中上方的散点表AODV协议的容错能力，下方散点表示DSR协议表示容错能力。可以看出，不同的逻辑容错策略，在相同的网络结构下，容错策略和整网的弹性水平之间存在线性或非线性关系。因此，本文可以借助机器学习方法，在已知容错策略部署方案的情况下，对整网的弹性做出预测。仿真试验生成的训练样本如表4所示。

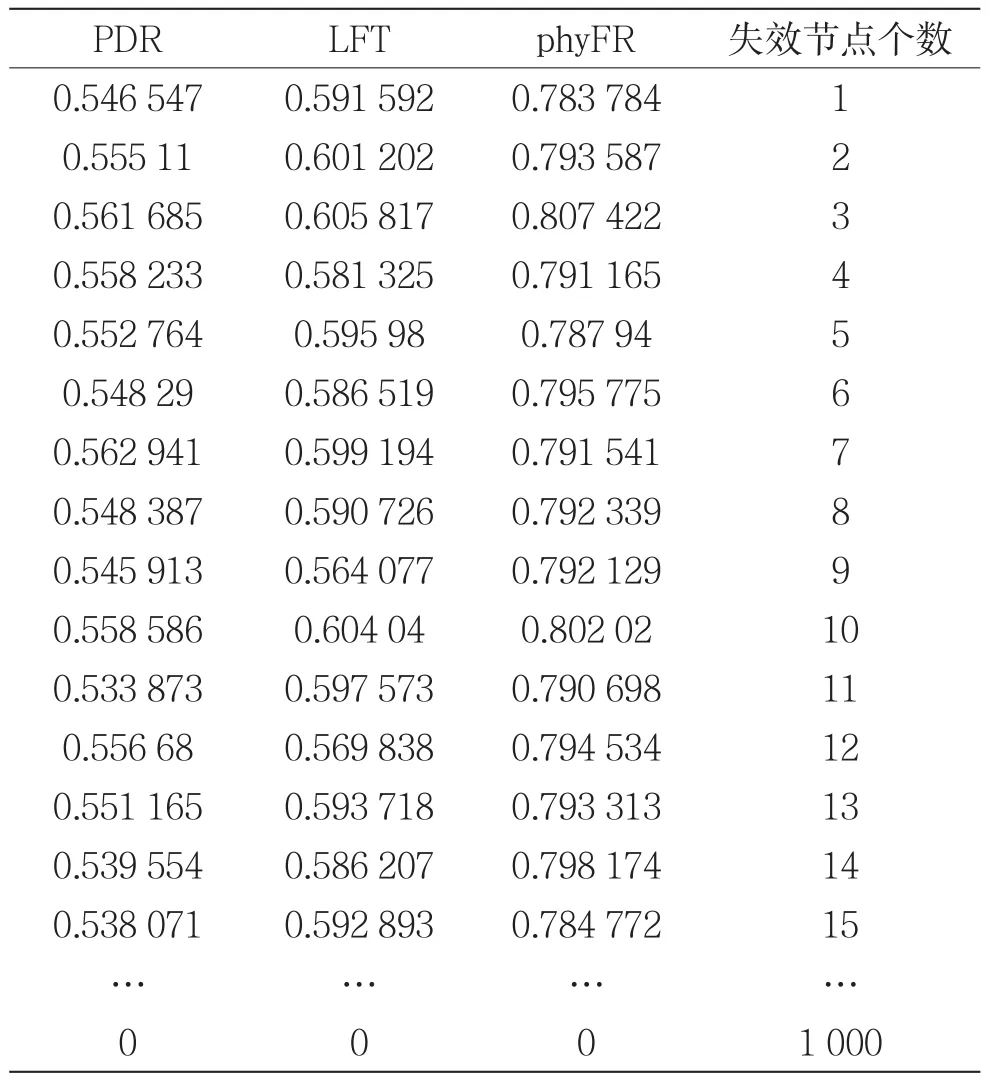
表4 仿真试验生成的训练样本

表4是根据网络时空动态模型和容错策略模型，在NS3上根据表3的配置生成的用于训练超限学习机的样本数据。在初始化步骤，本文借用python平台sklearn包中的train_test_split()方法，将原始结构化数据按照比例随机分割为训练集和测试集，这里采用30%的测试集比例进行交叉验证。

在得到训练数据后，可以对模型进行训练，从而得到一个良好的弹性预测模型。通过训练得到的模型精度可以满足预测需要：训练集准确率达到97.07%，交叉验证中测试集准确率达到96.43%。从结果可以看出，本文提出的方法在通过容错策略预测网络弹性方面具有较高的准确性。

在得到预测模型的基础上，进一步可以尝试根据单容错策略因素对整网的弹性水平进行预测分析，以期通过单容错机制对整网弹性的影响分析和多容错机制耦合影响下对整网弹性影响进行对比。从以上结果不难看出，网络弹性是多种容错策略共同作用的结果，容错策略间的互相耦合影响因素也会对整网的弹性造成影响。这一发现可以对网络设计阶段的容错设计提供支持：考虑容错策略间的耦合因素，将有助于选择更合理的容错策略组合，从而最大程度提升网络的可靠性。

4 结 语

本文结合网络弹性理论和极限学习机，提出了对网络弹性进行预测的方法。经实验验证表明：

（1）基于网络时空动态特征建立起的容错策略模型，可以有效描述和量化网络不同层面容错策略的容错能力；

（2）提出的基于机器学习的弹性预测方法可以通过容错策略量化参数准确预测网络弹性，准确率达到96%以上；

（3）通过对实验结果的初步分析，从数据层面可以得出，网络弹性是多个容错策略互相耦合作用的结果，多个容错策略内部的互相影响也会对整网弹性产生影响。

[1] Al-Kuwaiti M,Kyriakopoulos N,Hussein S.A Comparative Analysis of Network Dependability,Faulttolerance, Reliability,Security,and Survivability[J].IEEE Communications Surveys Tutorials,2009(02):106-124.

[2] Chen I R,Speer A P,Eltoweissy M.Adaptive Fault-Tolerant QoS Control Algorithms for Maximizing System Lifetime of Query-Based Wireless Sensor Networks[J].IEEE Transactions on Dependable and Secure Computing,2011(03):161-176.

[3] Zheng Z,Lyu M R.Selecting an Optimal Fault Tolerance Strategy for Reliable Service-Oriented Systems with Local and Global Constraints[J].IEEE Transactions on Computers,2015(01):219-232.

[4] Zhou A,Liu M,Li Z,et al.Cross-layer Design with Optimal Dynamic Gateway Selection for Wireless Mesh Networks[J].Computer Communications,2015(01):69-79.

[5] JSterbenz J P G.Redundancy,Diversity,and Vonnectivity to Achieve Multilevel Network Resilience,Survivability,and Disruption Tolerance Invited Paper[J].Telecommun Syst,2014(05):17-31.

[6] Hosseini S,Barker K,Ramirez-Marquez J E.A Review of Definitions and Measures of System Resilience[J].Reliability Engineering & System Safety,2016(01):47-61.

[7] Sydney A,Scoglio C,Gruenbacher D.Optimizing Algebraic Connectivity by Edge Rewiring[J].Applied Mathematics and Computation,2013(01):5465-5479.

[8] Alenazi M J F,Sterbenz J P G.Evaluation and Improvement of Network Resilience against Attacks Using Graph Spectral Metrics[J].Resilience Week(RWS),2015(2015):1-6.

[9] Zhang D,Sterbenz J P G.Measuring the Resilience of Mobile Ad Hoc Networks with Human Walk Patterns[C].2015 7th International Workshop on Reliable Networks Design and Modeling(RNDM),2015:161-168.

[10] Rohrer J P,Jabbar A,Sterbenz J P G.Path Diversification for Future Internet End-to-End Resilience and Survivability[J].Telecommun Syst.,2013(08):49-67.

[11] James D,Babu J J,Joseph S S.Literature Survey on Establishing Wireless Sensor Networks Using Otway Rees Protocol[J].International Journal of Emerging Trends in Science and Technology,2015(02):1815-1818.

[12] Rong B,Sun S,Kadoch M.Traffic Prediction for Reliable and Resilient Video Communications Over Multi-Location WMNs[J].J Netw Syst Manage,2016(06):516-533.

[13] Gao J,Barzel B,Barabási A L.Universal Resilience Patterns in Complex Networks[J].Nature,2016(02):307-312.

[14] Chen Y,Yang H.Sparse Modeling and Recursive Prediction of Space-Time Dynamics in Stochastic Sensor Networks[J].IEEE Transactions on Automation Science and Engineering,2016(01):215-226.

[15] Alenazi M G F,Sterbenz J P G.Evaluation and Comparison of Several Graph Robustness Metrics to Improve Network Resilience[C].2015 7th International Workshop on Reliable Networks Design and Modeling(RNDM),2015:7-13.

[16] Das R,Wales D J.Machine Learning Prediction for Classification of Outcomes in Local Minimisation[J].Chemical Physics Letters,2017(01):158-164.

[17] Huang G B.What are Extreme Learning Machines?Filling the Gap Between Frank Rosen blatt’s Dream and John von Neumann’s Puzzle[J].Cogn Comput,2015(06):263-278.

[18] Waxman B M.Routing of Multipoint Connections[J].IEEE Journal on Selected Areas in Communications,1988(12):1617-1622.

[19] Alenazi M J F,Sterbenz J P G.Comprehensive Comparison and Accuracy of Graph Metrics in Predicting Network Resilience[C].Design of Reliable Communication Networks(DRCN),2015:157-164.

[20] Ip W H,Wang D.Resilience Evaluation Approach of Transportation Networks[C].International Joint Conference on Computational Sciences and Optimization,2009:618-622.

[21] Tamura S,Tateishi M.Capabilities of a Fourlayered Feed forward Neural Network:Four Layers Versus Three[J].IEEE Transactions on Neural Networks,1997(03):251-255.