供水隧道围岩弹性抗力参数研究

(抚顺县投资审计中心， 辽宁 抚顺 113006)

岩石弹性抗力系数以及围岩质量分级，是对隧道工程影响较大的两个因素[1]，对隧道衬砌的设计起着决定性作用[2]。衬砌受到竖直方向压力后，围岩对衬砌产生反方向力的作用，而该反力反过来挤压衬砌，导致衬砌发生形变[3]。研究衬砌与围岩间力的作用，有利于对衬砌进行优化设计[4-5]。上世纪90年代，陈隽[6]等在不考虑横向裂隙不发育情况下，运用塑性理论及弹性理论，推导出具有通用价值的围岩抗力计算公式；方钱宝[7]等在前人理论研究的基础上，基于统一强度理论，对非均匀应力场下围岩的抗力系数进行了推导，引入地应力侧压力系数的概念，并通过试验发现围岩抗力系数在隧道的同一断面不同部位存在着差异性，最大限度地节约了成本；唐爱松[8]等对小浪底砂岩的动静弹性模量进行了分析研究，探讨了弹性模量与循环加荷间的关系，给出了小浪底砂岩的动静弹性模量关系式。本文基于相关理论研究，结合现场试验，对辽宁东部供水隧道实际工程中的围岩级别及弹性抗力系数进行相关性研究，并利用钻孔技术对相关岩石物理力学性质参数及波速值等进行物探测试，得到了不同岩性下塑性模量的试验值，确定了供水隧道围岩级别，最后通过对石英闪长岩和凝灰岩的变形模量及单位弹性抗力系数间关系的研究分析，得到了二者间线性关系，为今后相关工程的实施提供数值参考。

1 模型建立及相关物性试验

1.1 围岩抗力系数理论模型的建立

由胡克定律，可得围岩弹性塑性区交界面应力关系为

(1)

假设隧道围岩塑性区体积应变为零，即有εz=0，存在

(2)

而隧道塑性区围岩满足Mises屈服条件，假定υ=1/2，带入式(2)，即得塑性区本构方程为

(3)

塑性区变形为弹性变形与塑性变形之和，由弹塑性理论，可得：

(4)

求解极坐标下平面问题塑性理论物理方程，得到塑性区内塑性变形与弹性变形为

(5)

由此得到塑性衬砌与围岩接触处径向位移，并由文克尔假定求得围岩抗力系数的计算公式为

(6)

1.2 岩体力学性质试验

弹性波在岩体中传播时，会由于不同的岩体结构而对波速产生不同程度的削弱，利用岩体声波测试仪对波速进行测量，并综合考虑岩石的风化程度、构造以及时代等因素，得到的声波测试试验成果见表1。由表1数据可知，弹性波在石英闪长岩中的传播速度最大为5063m/s。

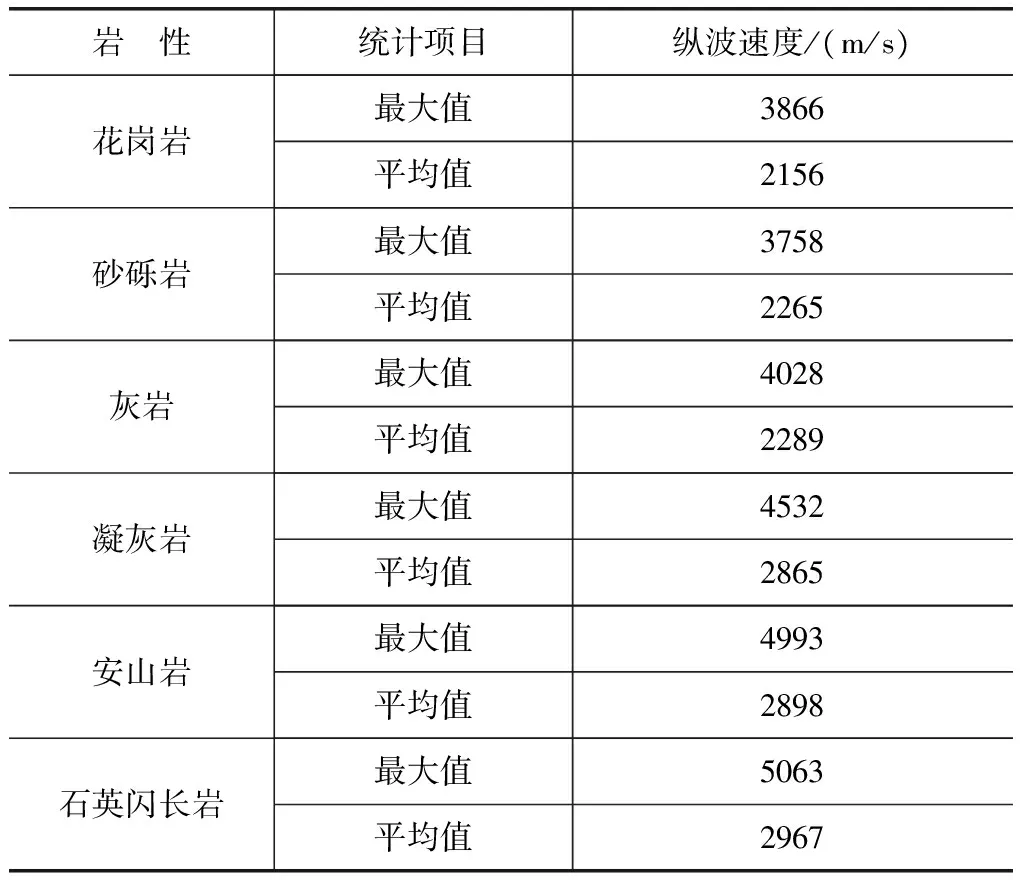
表1 声波测试试验成果

利用点荷载试验仪对岩体的点荷载强度进行测试，试验仪由外部加压油泵和圆台加荷装置构成，对不同岩性的试样进行测试，得到的点荷载测试试验成果见表2，由表2数据可知，凝灰岩的点荷载强度最大为221MPa。

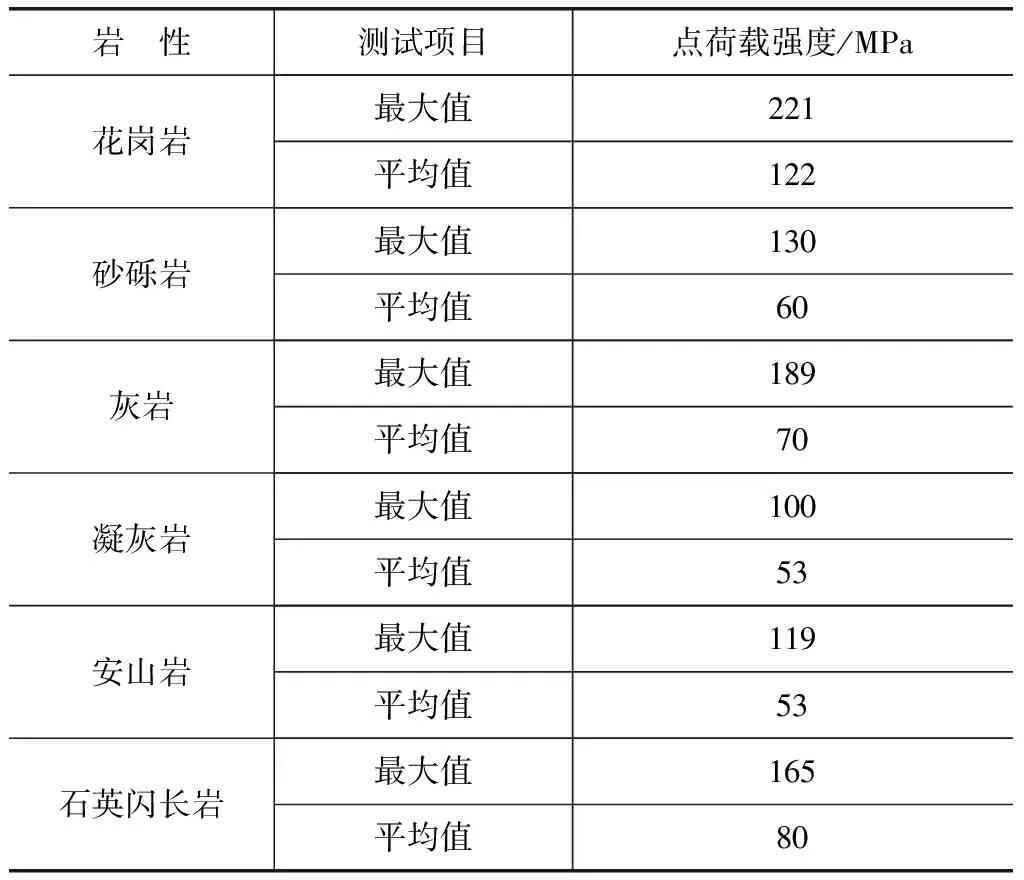
表2 点荷载测试试验成果

2 隧洞围岩分级

2.1 工程岩体质量分级方法

利用国标法确定岩体基本质量指标BQ值，选取相关修正因素，结合实际工程特点，确定各类工程岩体质量指标修正值，将岩体划分为5类(见表3)。

表3 岩体基本质量分级

围岩基本质量指标(BQ)确定的级别与基本质量定性特征存在差异时，首先确定岩体的基本质量级别，再根据公式BQ=100+3Rc+250kv计算岩体基本质量指标(BQ)，对其计算结果进行分类，可作为岩体级别。

2.2 隧洞围岩级别的确定

当受到高初始应力以及地下水的影响时，应对岩体的基本质量指标(BQ)进行相关性修正，并对其结果进行等级分类。利用公式[BQ]=BQ-100(K1+K2)计算岩体基本质量指标值，其中K1、K2分别为地下水修正系数与初始应力状态修正系数，其值见表4。

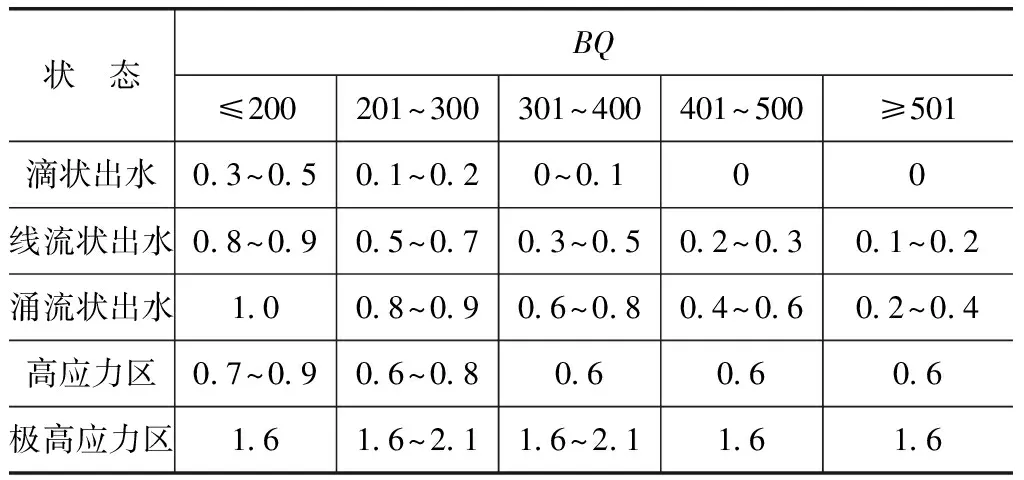
表4 地下水与初始应力状态影响修正值

对工程中涉及到的围岩进行分类，见表5。

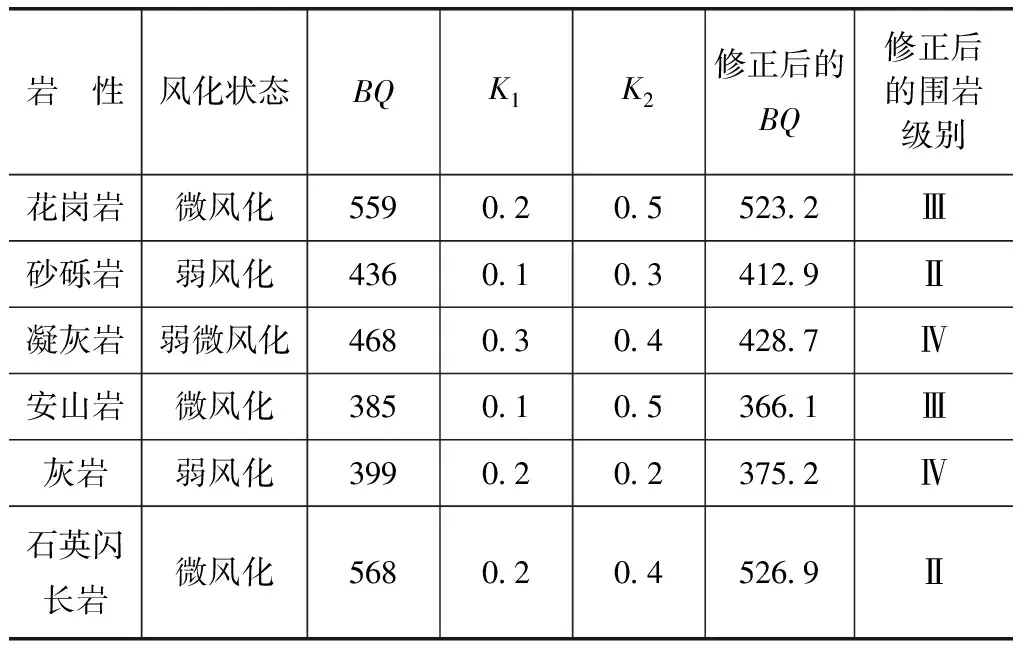
表5 隧道围岩分级

3 岩石弹性抗力系数研究

3.1 岩石弹性抗力系数试验方法

采用径向液压枕法作为岩石弹性抗力试验方法，除去岩体表面的松散岩块，模拟隧道在均匀内压下的受力状况(见图1)。利用柔性加压枕进行加压时，在混凝土条块间预留缝隙，以免由于混凝土条块相互作用引起变形。压力经加压枕一侧由混凝土传向隧道围岩，而另一侧则作用于刚性反力架，由径向压力值及围岩变形数值即可计算岩体的单位抗力系数。

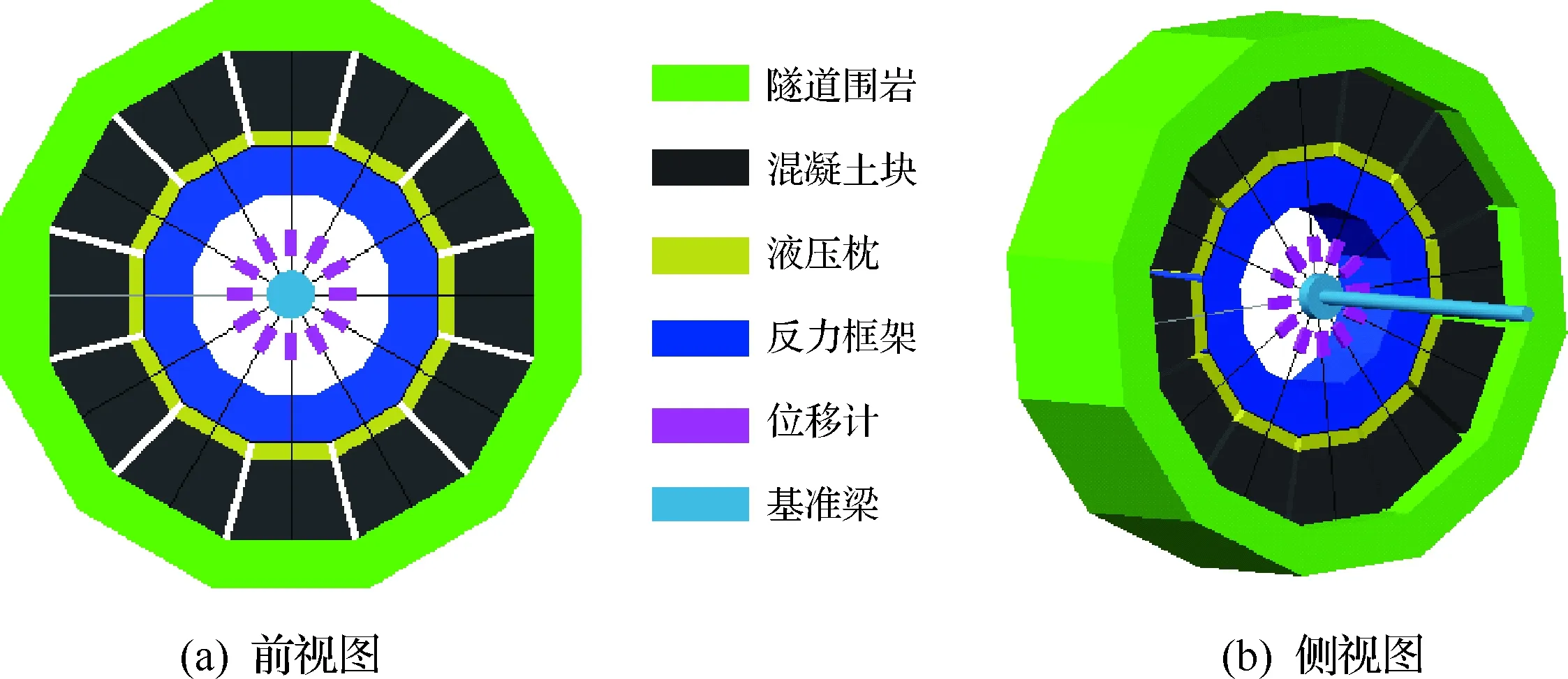
图1 径向液压枕法

3.2 试验成果分析

利用隧道岩石弹性抗力系数计算公式求得围岩单位弹性抗力系数K0，并对变形模量E0进行计算，相关计算公式为

(7)

式中k0——单位弹性抗力系数；

Φ——变形修正系数；

p——围岩表面所受单位应力,MPa/cm；

ΔR——围岩表面径向位移平均值,cm；

E0——变形模量；

u——岩石泊松比。

选取较为重要的凝灰岩与石英闪长岩作为试验测试的对象，在对凝灰岩进行分析研究时，测量隧道各部位在径向荷载作用下产生的径向变形值，对其结果进行绘制，见图2，由图2可知，第一测量断面和第二测量断面在径向压力作用下，实测围岩径向变形比第三测量断面大得多，第三测量断面围岩径向变形程度较小，说明各个测量断面间的岩性存在很大的差异，第二、第三测量断面的岩性要优于第一、第二测量断面。

图2 各测量断面径向变形分布曲线

凝灰岩在不同径向压力下的变形值、抗力系数和变形模量见表6，取泊松比μ=0.33，变形修正系数为0.86，隧道半径R=1.55m。由表6可知，随着径向压力值的增大，凝灰岩产生的变形值也随之增大，其单位抗力系数值越来越小。

石英闪长岩在径向压力下的变形值、抗力系数和变形模量见表7，泊松比μ=0.24，变形修正系数为0.778，由表7可知，石英闪长岩的单位抗力系数K0随着径向压力的变大而减小，形变值则随着压力增大而增大。

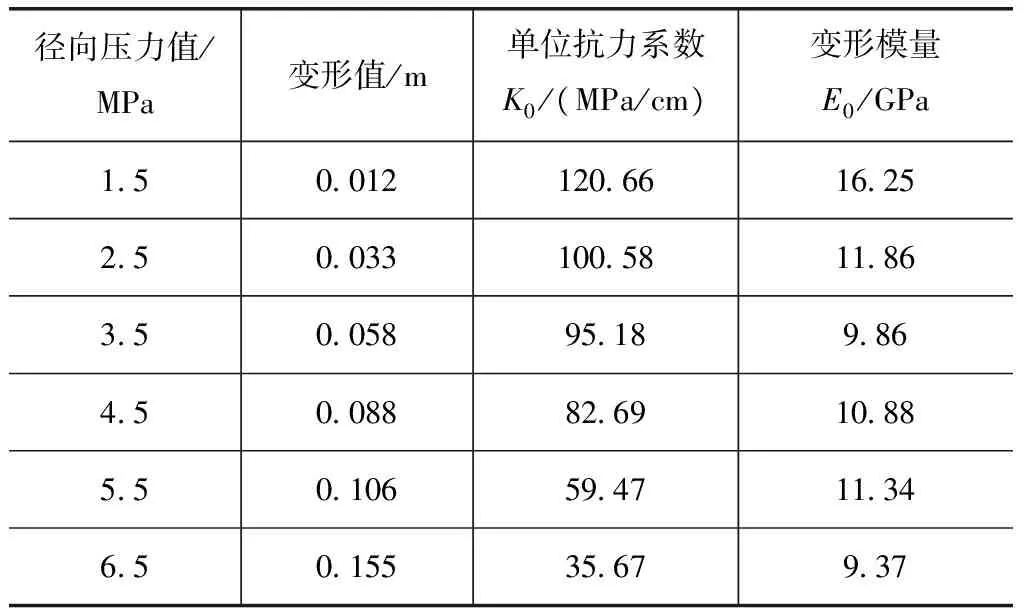
表6 不同径向压力下凝灰岩岩体变形模量E0和单位抗力系数K0

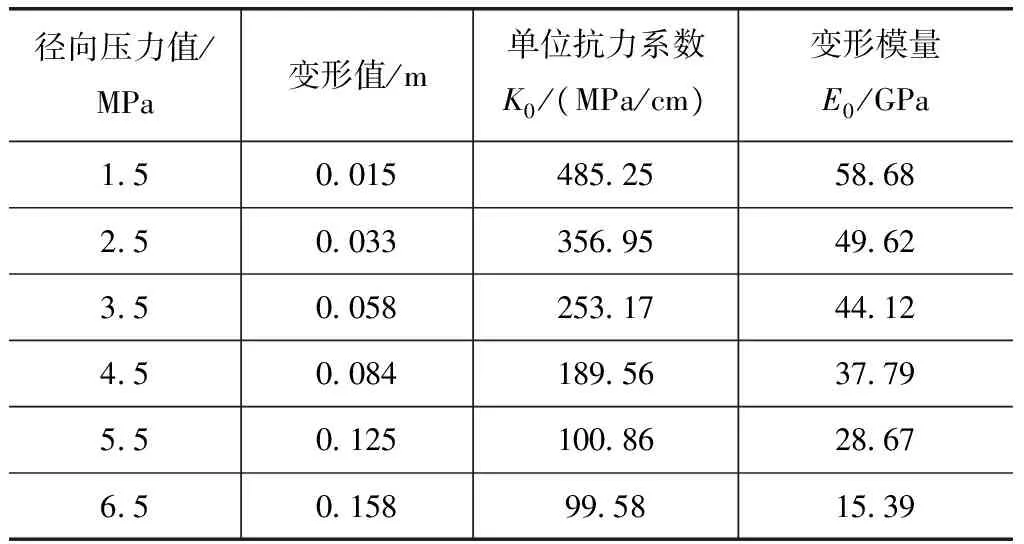
表7 不同径向压力下石灰闪长岩岩体变形模量E0和单位抗力系数K0

凝灰岩岩体的单位抗力系数范围为35.67～120.66MPa，变形模量范围为9.37～16.25GPa。石英闪长岩岩体的单位抗力系数范围为99.58～485.25MPa，变形模量范围为15.39～58.68GPa。图3为石英闪长岩与凝灰岩变形模量和单位弹性抗力系数关系，由图3可知，两种岩性下的变形模量与单位抗力系数间呈线性关系，二者单位抗力系数都随着变形模量的增大而增大，且石英闪长岩的变化率要大于凝灰岩。

图3 岩石变形模量与单位抗力系数关系

4 结 论

基于相关理论模型，结合大量室内岩石力学试验，对隧道围岩级别及岩石弹性抗力系数进行了计算分析，对弹性波在岩体中的传播速度及点荷载强度等做了测量，并对围岩分级的方法BQ法进行了详细阐述，提出了相应的岩体质量级别，最后通过对地下水与初始应力状态修正值的计算，明确了不同岩性岩石修正值的大小，得到了修正后的岩石分类。通过试验得到了凝灰岩与石英闪长岩的变形模量和单位弹性抗力系数，并对其相关性进行分析，得到了石英闪长岩与凝灰岩岩体单位弹性抗力系数与变形模量间的近似线性关系，并通过对比发现两种岩性岩石的单位弹性抗力系数均随着变形模量的变大而增大。

[1] 余世为,刘成禹.基于地震波法测定岩体弹性抗力系数[J].现代隧道技术,2017(1):68-73.

[2] 汪洪泉.超长水工隧洞TBM法开挖施工供电方法探讨[J].中国水能及电气化,2015(4):22-24.

[3] 焦景辉,赵宪女,薛兴祖.中部城市引松供水工程总干线围岩弹性抗力系数试验及参数选取[J].水利与建筑工程学报,2015(1):109-113.

[4] 马鹏,卢泳,陈文华,等.某水电站围岩弹性抗力系数试验研究[J].水利规划与设计,2014(2):81-83,10.

[5] 王芝银,袁鸿鹄,汪德云,等.基于量测位移的隧洞围岩弹性抗力系数反演方法[J].工程地质学报,2013(1):143-148.

[6] 陈隽,王琴,李杰.地下管线地震响应及土体弹性抗力系数研究[J].地下空间与工程学报,2012(3):499-504,607.

[7] 方钱宝,马建林,喻渝,等.大断面黄土隧道围岩弹性抗力系数、变形模量与压缩模量试验研究[J].岩石力学与工程学报,2009(S2):3932-3937.

[8] 唐爱松,李敦仁,钟作武,等.岩滩电站岩体弹性抗力系数试验研究[J].岩石力学与工程学报,2005(20):163-167.