电火花穿孔机群孔加工路径规划算法
夏蔚文,黄广炜,王军旗,赵万生
(上海交通大学机械与动力工程学院,机械系统与振动国家重点实验室,上海200240)
高速电火花小孔加工被普遍用于加工微小孔、群孔、斜孔、深孔等,在航空航天、模具制造等领域广泛使用[1]。在群孔加工时,电极从第一个孔开始,依次移动到下一个孔位放电加工,需频繁地在孔位之间移动,整个加工任务中累积的移动距离可达数米,累积的移动时间也十分可观,加工的整体效率往往会因为不当的路径规划而大幅降低。在电火花小孔加工机床数控编程时,大多数会通过DXF绘图文件保存图形和点位信息。CAM软件读取图中孔位信息后,经过路径规划处理,输出为G代码或其他格式加工代码用于加工。但在DXF文件格式中,实体的排列顺序由图元绘制的先后次序决定,如果整体图形复杂,或在绘制过程中出现反复修改,则加工次序与图中排列不一致,这是导致加工轨迹过长的重要原因之一。在机械钻孔加工中也存在类似的问题,一些学者进行了讨论。朱光宇提出一种基于粒子群优化算法的钻孔路径规划方法,具有全局收敛的特性[2-3]。刘晋飞针对蜂窝陶瓷模具钻孔加工问题,基于均匀分布理论开发了一套CAD/CAM系统,提高了轨迹生成效率[4]。陈恋芳提出了一种基于差分算法的群孔加工路径优化方法,同时考虑了钻孔加工中更换刀具的情况[5]。Abbas等针对矩形阵列群孔,使用蚁群优化算法获得了最优解[6]。
本文以有效和实用为原则,参考旅行商问题近似解法,考虑孔的相对距离或坐标,提出了几种群孔加工轨迹规划的方法,并集成到小孔电火花加工机床的CAM软件中。几种算法的比较测试结果表明,规划后的加工轨迹长度比未规划时显著减少,且各个算法的时间复杂度均可接受。
1 群孔路径规划问题的抽象
设孔数为n,构成集合V。在加工顺序中,任意两点可相邻且无先后限制。因此,集合V中可定义一个二元关系,表示两点在加工时相邻:

且A为对称关系。A、V构成无向完全图:

给每条边 a=(vi,vj)赋权为 w(vi,vj) ,代表任意两点间的距离,得到无向完全网络(G,w)。
群孔加工的最短路径规划要求在此无向网络中,以指定的节点为起点,搜索一条道路经过剩余所有节点一次且仅仅一次,不回到初始节点,且带权路径的长度最小。
此问题类似于旅行商问题 (Traveling Salesman Problem,TSP)。TSP要求在带权无向完全网络的众多Hamilton回路中寻找带权长度最短的一条。该问题在数学上属于非确定多项式 (Non-deterministic Polynomial,NP)完全问题,目前没有多项式时间复杂度的精确解法。在众多近似解法中,许多学者研究了遗传算法、模拟退火算法、神经网络算法、进化算法等[7]。
群孔加工路径规划问题与TSP的区别在于:①指定了起点;②不必返回起点,形成回路。因而群孔加工路径规划问题获得最优解仍非常困难,但仍可借鉴TSP近似算法达到良好的效果。下文将在第二节和第三节介绍两种TSP近似算法在群孔路径规划问题中的应用,并在第四节介绍基于坐标排序的路径规划算法。
2 最近邻法
最近邻法是指:从节点v1出发,找到其未被标记的最邻近的节点v2;再从v2出发,寻找最邻近节点v3;直到遍历所有节点,抵达vn,从而获得一条遍历各点的道路,其流程见图1。由于需计算任意两点间的距离,最近邻法的时间复杂度为 T(n)=O(n2)。
3 插入法
插入法的思路是:从节点v1出发,维护一个已标记的节点集合T,根据未标记节点到节点集合的距离,从中选取一点vj,插入已标记的节点集合中。
其流程可表述如下:所有节点构成无向完全图G=(V,E),|V|=n;vj表示第 j个节点; 每边的权为 w(vi,vj)。
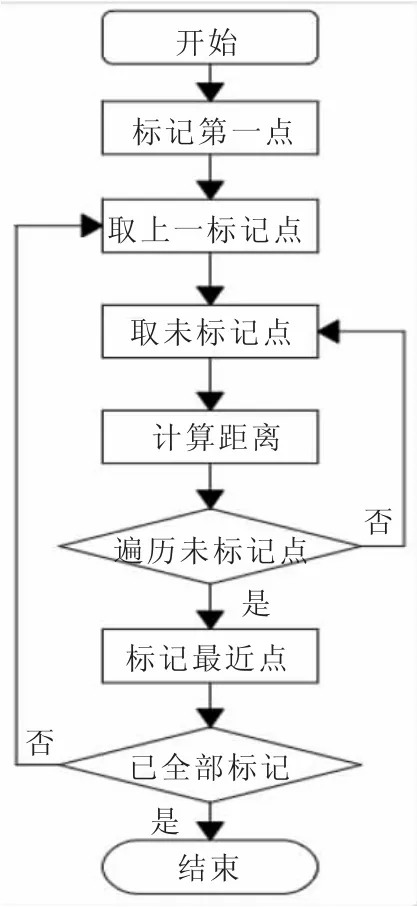
图1 最近邻规划法
(1)初始标记节点集合为T={v1},初始轨迹记为H=(v1)。
(2)在|T|<n 时循环。
(3)对所有 vi∈V-T,计算 vi到 T 的距离,为:
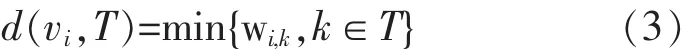
(4)选取待插入节点vj和插入位置t:
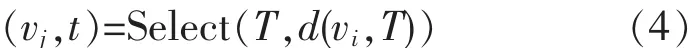
(5)插入集合T和轨迹H:
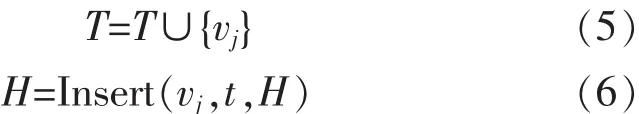
(6)结束。
依据选取插入点和插入方法的不同,插入法又可分为最近插入法和贪心插入法等。
插入法每次循环时,需计算、比较已标记节点中任意一点和未标记节点中任意一点之间的距离,总运算次数为:可得插入法的时间复杂度为 T(n)=O(n3)。
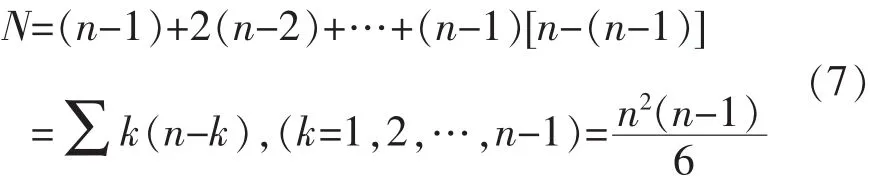
3.1 最近插入法
最近插入法选取未标记节点中距离当前标记节点集合T最近的节点:
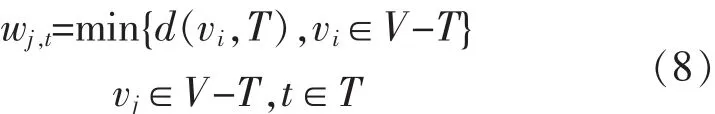
然后将选取的未标记节点插入t的后面。设H=(…t1,t,t2…),则插入后得到 H=(…t1,t,vj,t2…)。
3.2 贪心插入法
与最近插入法相同,贪心插入法选取未标记节点中距离当前旅行圈T最近的节点,再采用贪心策略插入当前轨迹 H。 设 H=(…t1,t,t2…),若:
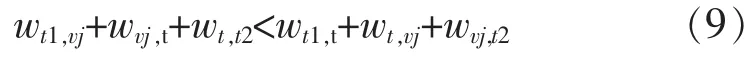
即:
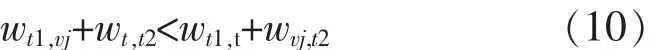
则将vj插入t的前面,否则插入t的后面。
由于轨迹中第一节点被指定为不可更改,如果t恰好为第一节点,则只能插入t的后面。
4 坐标排序规划法
考虑到群孔加工时的点位信息以各点坐标表示,对于群孔排列较密集且按阵列排布的情况,可不计算各点间距离,而是直接通过坐标排序来规划路径。坐标排序法的流程如下:
(1)以指定第一点为原点,将剩余各节点划分到四个象限中。落在坐标轴上的点,可按需划入相邻象限之一,可获得四个节点子集 V1、V2、V3、V4。
(2)V1中按各点x坐标升序排序,然后按x坐标分组。设定分组宽度,记为d,将x坐标位于[0,d),[d,2d)…的节点分别分组。设V1中最右侧节点的x坐标为xmax,则共得到[xmax/d]+1组,并以x升序从1开始编号。将编号为奇数的组中的节点,按y坐标升序排序;编号为偶数的组中的节点,按y坐标降序排序。
(3)V2、V3、V4中的节点按同样的分组宽度分组。各组中的节点也按y坐标排序。其中,V2中各组的排序方式与V1相同;V3、V4中的各组以x降序从1开始编号,且奇数组内按y坐标降序排序,偶数组内按y坐标升序排序。
(4)按 V1、V4、V3、V2的顺序,按各子集中的分组编号升序,将各组的节点添加到轨迹中。
在坐标排序法中,不需计算各点间的距离,只需将除第一点外的所有点分别按x和y进行排序,且使用快速排序算法。因此,坐标排序法的时间复杂度为 T(n)=O(nlogn)。
5 方法验证
上述方法被集成到基于LibreCAD开发的电火花穿孔机CAM软件中。实验选取2个群孔图形进行路径规划测试,第1个图形为图2所示的阵列,孔位分别位于圆心处,阵列中有10排10列共计100个单元、600个孔位;第2个图形为图3所示的多边形阵列,孔位位于顶点处,共有1632个孔位。
测试环境分别为PC机和嵌入式控制器,参数见表1。测试时,对相同的图形分别采用不同的算法进行规划,记录算法运行时间和最终获得的路径长度。针对每种环境中的每个图形,四种算法均运行五次,顺序随机,记录其运行的平均时间。将不同算法的运行时间进行比较,并将各算法得到的路径长度与未进行路径规划时的路径长度比较,得到的结果见表2~表5。可看出,采用坐标排序法的耗时最少,只需不到1 ms即可完成规划,但规划效果不如其他几种方法。该方法对于按阵列排列的图形(图2),在减少路径长度方面的效果较明显,但对于复杂图形(图3),其效果较差。采用最近邻法的耗时也少,且对于不同图形的规划效果都十分显著,可减少运动路径30%以上。
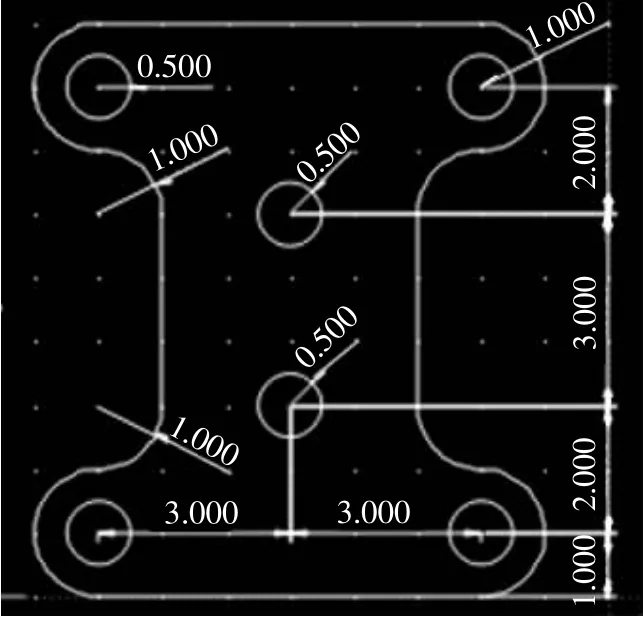
图2 测试图形1

图3 测试图形2

表1 测试环境
此外,两种插入法的耗时都较长。处理1632个点位图形时,在嵌入式控制器上的运行时间已超过16 s。根据各算法的时间复杂度分析,随着点位的增加,插入法的耗时会急剧增大,且其规划效果并没有显著优于最近邻法。因此,在四种规划算法中,最近邻法最为实用和有效,而在处理线性阵列图形时,使用坐标排序法也未尝不可。
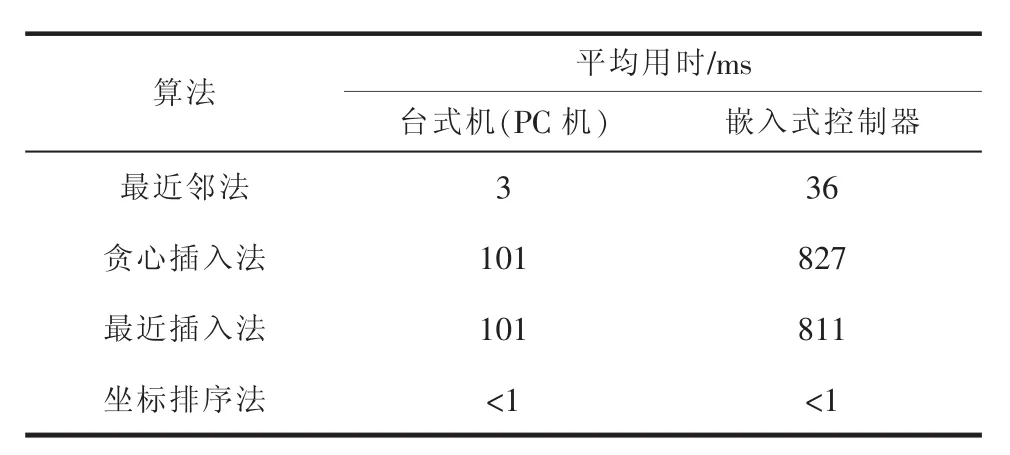
表2 图形1路径规划用时
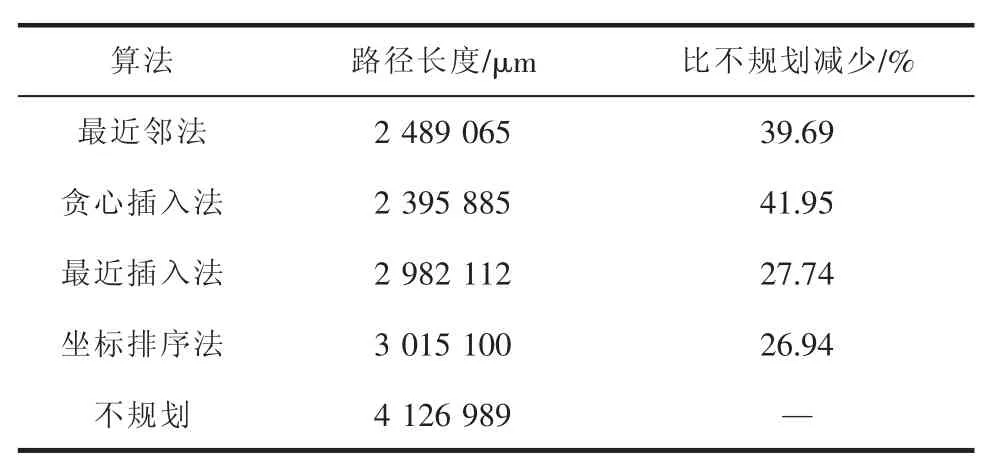
表3 图形1路径规划结果

表4 图形2路径规划用时
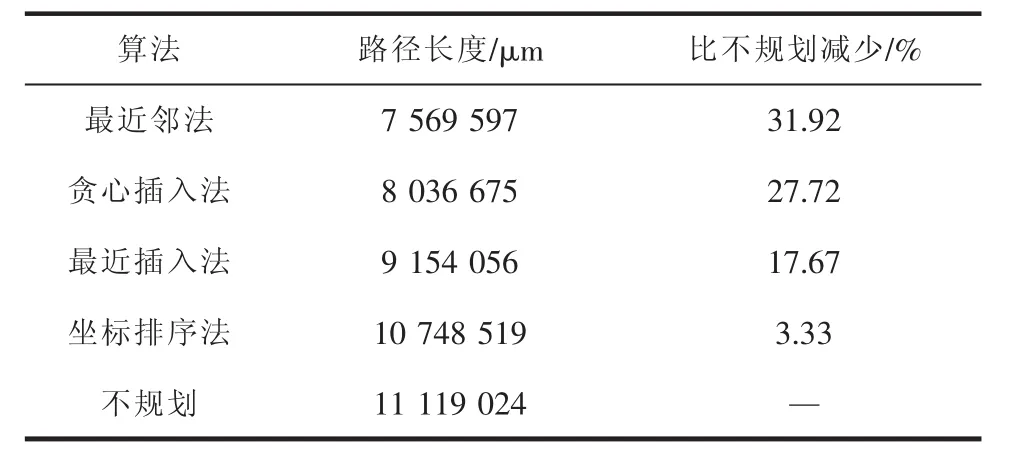
表5 图形2路径规划结果
6 结束语
针对电火花群孔加工时的路径规划问题,根据各点相对距离和坐标,参考TSP近似解法,提出了几种有效且实用的规划算法。通过在不同环境中针对不同加工图形的测试表明,几种算法均能比不规划时减少电极运动距离、提高整体效率,且算法运行时间均可接受,其中最近邻法运算耗时短,规划效果好,故最为实用。
[1] 赵万生,刘晋春.电火花加工技术[M].哈尔滨:哈尔滨工业大学出版社,2000.
[2] 朱光宇.面向钻削路径规划问题的微粒群优化算法研究[J].信息与控制,2008(1):103-107,112.
[3] ZHU G Y,ZHANG W B.Drilling path optimization by the particle swarm optimization algorithm with global convergence characteristics[J].International Journal of Production Research,2008,46(8):2299-2311.
[4] 刘晋飞,姚平喜.基于均布的群孔加工CAD/CAM系统的研究与开发[J].精密制造与自动化,2009(3):52-54.
[5] 陈恋芳.基于差分算法的群孔加工工艺优化 [D].福州:福州大学,2011.
[6] ABBAS A T,ALY M F,HAMZA K.Optimum drilling path planning for a rectangular matrix of holes using ant colony optimisation[J].International Journal of Production Research,2011,49(19):5877-5891.
[7] HOFFMAN K L,PADBERG M,RINALDI G.Traveling salesman problem [M].Encyclopedia ofOperations Research and Management Science.Springer US,2013:1573-1578.

