不同光线入射角度下超声速湍流边界层气动光学效应的实验研究∗

丁浩林 易仕和 朱杨柱 赵鑫海 何霖

1)(国防科技大学航天科学与工程学院,长沙 410073)2)(解放军63926部队,北京 100192)3)(解放军理工大学爆炸冲击防灾减灾国家重点实验室,南京 210007)(2017年7月11日收到;2017年8月22日收到修改稿)

1 引 言

高速流场可压缩性引起的气动光学效应对于发展(高)超声速飞行器机载光学探测系统影响很大,在数十年中引起了广泛的关注[1−3].在大多数气动光学效应的研究中,光程差(optical path difference,OPD)经常被用于表征气动光学效应的强弱程度.湍流边界层作为气动光学效应研究中最重要的内容之一,自20世纪50年代以来,由其引起的气动光学效应已经得到了较为深入的研究[4].湍流边界层气动光学效应的研究者主要采用两方面的技术实现对其气动光学效应的研究:数值仿真方法和实验测量方法.在发展初期,受到计算能力的限制,气动光学数值仿真主要采用雷诺应力平均(Reynolds averaged Navier Stokes,RANS)方法,只是此种方法无法有效反映流动中涡结构对气动光学效应的影响,应用范围有限.随着计算能力的不断进步,大涡模拟(large eddy simulation,LES)方法以及直接数值模拟方法逐渐得到推广,并且应用于气动光学效应研究中.Tromeur等[5,6]采用LES方法研究了亚声速(Ma=0.9)和超声速(Ma=2.3)湍流边界层的气动光学效应,亚声速湍流边界层的数值计算结果与实验数据在光学畸变幅值方面符合较好.Wang等[7]利用可压缩LES方法研究了亚声速(Ma=0.5)湍流边界层引起的气动光学效应,获取了较为详尽的密度脉动和波前统计数据,包括光程差空间均方根值OPDrms数据、空间和时间相干性以及频率谱信息.总体而言,当前计算能力仍然限制着高速条件下的气动光学研究.

在实验研究方面,Wyckham和Smits[8]利用二维Shack-Hartmann波前传感器测量了跨声速和高超声速边界层的气动光学波前.通过假设边界层内压力脉动可以忽略并且引入强雷诺比拟,提出了一种边界层气动光学效应相似律.Gordeyev等[9,10]利用Malley探针技术测量了马赫数在0.3—0.95之间的湍流边界层的气动光学效应,并且对Wyckham和Smits提出的气动光学相似律做出了进一步的验证和改进,这种相似律在后文中被用于校验本文气动光学畸变测量数据的可靠性.

最近几年,我们团队发展了一种利用基于纳米粒子的平面激光散射(nano-particle-based planar laser scattering,NPLS)技术进行流动密度场测量的方法.这种方法已经成功应用于测量超声速绕流和超声速边界层的密度场[11−13].由于其具有高时空分辨率的特点,可以清楚地测量精细的流场结构和时间演化过程.故这种技术可以给气动光学研究提供很大的便利[11,12,14,15].

本文旨在基于NPLS技术获取的超声速湍流边界层密度场结果,研究不同光线入射角度下超声速湍流边界层气动光学效应的异同及其内部机理.下面首先简要介绍实验装置、基于NPLS的密度场测量方法、研究对象、气动光学相关原理以及光线追迹方法;再对湍流边界层气动光学波前测量结果的可靠性进行验证,并对不同光线入射角度下超声速湍流边界层气动光学效应的异同及其物理内涵进行讨论分析.最后,总结当前研究取得的相关结论.

2 实验装置

2.1 超声速风洞

图1为本文实验所采用的KD-03低噪声超声速风洞结构示意图,风洞的运行方式为吸气式,气源采用经过干燥除尘的空气,风洞试验段的截面尺寸为100 mm(宽)×120 mm(高),侧面尺寸为250 mm(长)×120 mm(高),并安装有高质量的光学玻璃以满足实验测试的需要[16].

风洞运行具体参数如表1所列.

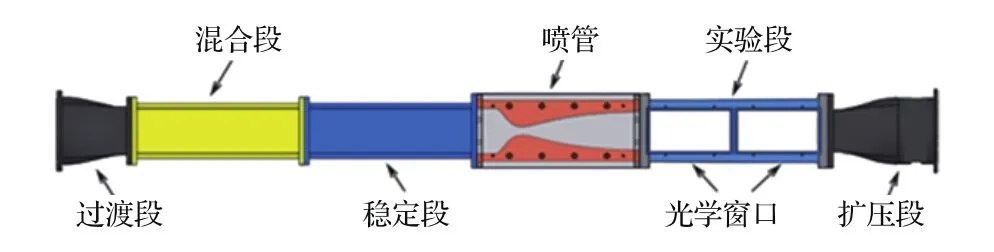
图1 KD-03超声速风洞结构示意图Fig.1.Schematic diagram of the KD-03 supersonic wind tunnel.

表1 风洞流场校测参数(1 atm=1.01325×105Pa)Table 1.Calibrated parameters of wind tunnel.

2.2 密度测量

采用基于NPLS技术的流场密度测量方法测量超声速湍流边界层的密度场.NPLS技术采用双腔Nd:YAG脉冲激光器作为光源,光线波长为532 nm,脉冲宽度为6 ns,片光单脉冲能量设置为250 mJ,片光最薄处厚度为0.5 mm,距离片光出光口500 mm.实验采用线传输的跨帧CCD相机成像,跨帧时间为5µs,获得原始图像大小为2048 pixel×2048 pixel,灰度级4096,拍摄帧频为5 Hz,曝光时间设置为5 ms,实际曝光时间由激光片光脉冲宽度决定,即6 ns,保证了流场测量结果的瞬时特性.纳米粒子在超声速流动中优异的跟随性能保证了其可以很好地反映流场的密度变化情况.在去除诸如背景、暗信号以及不均匀的片光强度等因素对NPLS测量的影响,可以构建NPLS图像灰度和当地流场密度之间的关系,并且利用斜激波校正的方法对获取的关系进行进一步的校正,最后,便可以定量测量超声速流场中某个特定截面的密度场[12,14,15].更多关于利用NPLS测量超声速流场密度的技术细节可以参考文献[11].

2.3 实验边界层

本文选取风洞喷管下游180 mm处的下壁面湍流边界层作为研究对象.此边界层在喷管上游就已经自然转捩为湍流,到达实验段时,边界层已经完全湍流化.图2为实验装置示意图,实验段下壁面安装的光学玻璃可以有效减小壁面反光对于测试结果的影响.x轴正方向定义为流动的方向,y轴正方向定义为垂直于风洞壁面向上的方向,利用右手定律建立如图2所示的正交坐标系.故可以定义x-y平面为流向平面,流动方向从左到右.

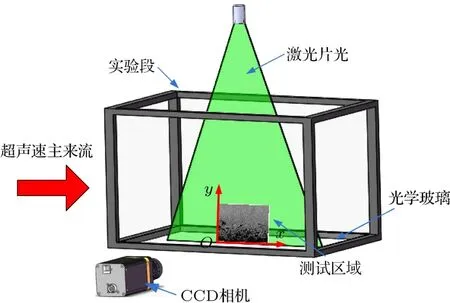
图2 实验装置示意图Fig.2.Schematic of experimental arrangement.

2.4 基本原理和光线追迹方法

基于Gladstone-Dale关系式,可以根据湍流边界层的密度场获取其对应的折射率场,即

这里n和ρ分别表示折射率和密度;KGD为Gladstone-Dale常数,在光线波长为532 nm,其值近似为2.22×10−4m3/kg.

光程(optical path length,OPL)表示为折射率n沿着光线传播路径L的积分,

在大多数情况下,OPD相比于OPL更为重要,OPD定义如下:

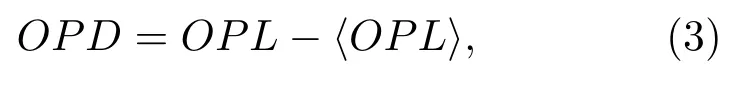
这里,尖括号表示孔径上的空间平均.OPD的空间均方根值OPDrms作为常用的气动光学效应强弱评价指标,应用十分广泛.

Jones和Bender[17]指出,如果光线波长小于湍流的最小尺度,光线追迹方法对于近场气动光学计算是有效的.图3为本文采用光线追迹方法计算的示意图,光线入射角度α可以被定义为光线入射方向和流动方向之间的夹角;Δx和Δy分别代表x轴和y轴的计算网格间距,更多关于计算细节的描述请见参考文献[1].

图3 二维平面光线追迹方法示意图Fig.3.Schematic of the ray-tracing method in the two-dimensional plane.

3 实验结果与分析

3.1 实验边界层波前测量有效性验证

图4所示为本文研究的超声速湍流边界层的瞬时密度结果,光线垂直入射时,可以获得如图5所示的OPD分布.实验测量范围为:x/δ≈0—2,y/δ≈0—1.5,边界层厚度δ=10.2 mm,图像空间分辨率为11.4µm/pixel.He和Gao利用Crocoo-Busemann关系式验证了实验获得的密度结果的有效性[13,14].

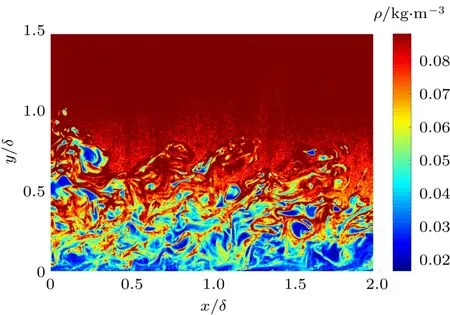
图4 (网刊彩色)NPLS技术获取的Ma=3.0湍流边界层瞬时密度场Fig.4.(color online)The instantaneous density fi eld of Ma=3.0 turbulent boundary layer obtained by NPLS.

图5 图4所示超声速湍流边界层对应的OPD(α=90°)Fig.5.OPD corresponding to the supersonic turbulent boundary layer shown in Fig.4(α =90°).

进一步分析之前,通过将实验测量的OPDrms与湍流边界层气动光学相似律的理论结果进行对比,检验实验测量结果的可靠性.这里采用由Wyckham和Smits[8]提出的OPDrms相似律,其可以表述为

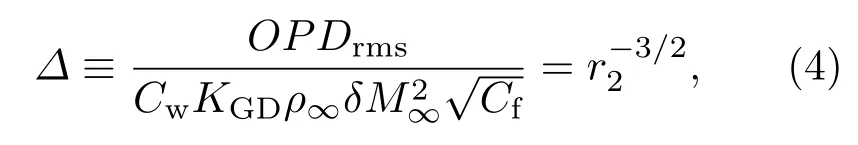
这里,Cf表示壁面摩阻系数;模型参数Cw=0.2;

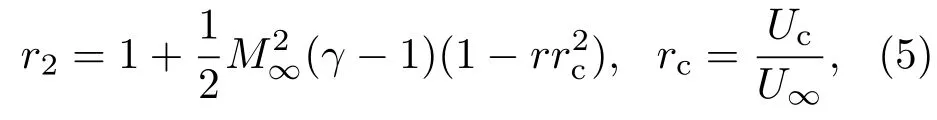
对于绝热壁面,γ=1.4为比热比,r=0.9表示恢复系数,Uc表示大尺度光学结构的对流速度.当使用相似律时,方程(4)左边项Δ由实验结果计算得到,右边项通过理论结果预测得到.利用Gordeyev等[9]的实验结果,对于亚声速边界层,rc=0.82,对于超声速边界层,rc=0.84.(4)式右边项在rc=0.82时其值为0.45,rc=0.84时其值为0.47.利用实验获得的100组OPDrms绘制如图6所示的箱体图,结果与气动光学相似律的理论计算结果符合良好.

图6 (网刊彩色)实验结果与理论结果的对比Fig.6.(color online)Comparison of experimental results with theoretical results.

3.2 光线入射角度对于气动光学效应的影响

在实际的应用中,通常无法保证光线总是垂直穿过流场区域.为了研究波前畸变与光线入射角度的关系,对不同光线入射角度下超声速湍流边界层的气动光学效应进行了研究.如图3所示,光线入射角α定义为光线入射方向和流动方向之间的夹角.当α＞90°时,光线倾斜着向上游入射;当α=90°时,光线垂直于边界层入射;当α＜90°时,光线倾斜着向下游入射.选择五种不同的入射角度α=60°,75°,90°,105°,120°进行研究,在每个角度下分别获取100组不同时刻的OPDrms.相关结果绘制成如图7所示的箱体图.从图7可以看出,气动光学畸变程度与光线入射方向密切相关,随着光线入射方向与壁面垂直方向之间角度的增大,气动光学效应逐渐恶化,并且基本关于壁面垂直方向(α=90°)对称分布.这种现象主要是由于当光线倾斜入射湍流边界层时,其在边界层中传输的距离增长,相比于垂直穿过增加了的名义传输距离,这也是导致光线倾斜入射湍流边界层时气动光学畸变加剧的主要原因.

图7 不同光线入射角下超声速湍流边界层OPDrms分布Fig.7.OPDrmsdistributions of supersonic turbulent boundary layer at different light incident angles.

如图8所示,不同光线入射角度下获取的不同时刻的OPDrms较好地满足正态分布的特点.然而,倾斜入射的光线积分路径增长,导致光线受到流场的干扰更为强烈.这种时间上的非定常性和空间上的非均匀性导致光线倾斜入射时对应的气动光学畸变在不同时刻的差异性增大,即分布曲线底部变宽,这实际上加大了气动光学效应校正的难度.所以,光线倾斜入射湍流边界层对应的气动光学效应一方面会随着倾斜角度的增加而变得更为严重,另一方面不同时刻获取的气动光学效应的差异性也会随之增加.这就需要在气动光学优化设计中尽量避免光线斜穿或者减小斜穿角度.

图8 (网刊彩色)不同光线入射角下超声速湍流边界层OPDrms概率分布图Fig.8.(color online)OPDrmsprobability distribution of supersonic turbulent boundary layer at different light incident angles.

从图7和图8可以发现,在光线入射方向与垂直壁面方向偏差相同角度时,光线倾斜向下游传输时湍流边界层的气动光学效应要强于光线倾斜向上游传输时对应的结果.为了进一步为深入地研究上述现象的内在机理,从最基本的气动光学联系方程出发,即

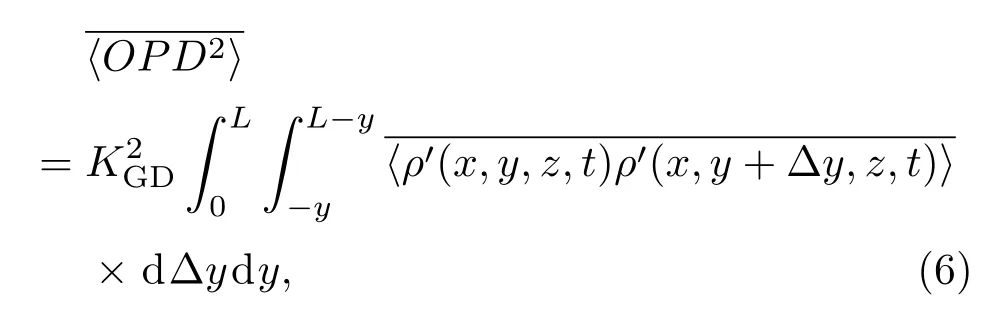
这里上划线表示时间平均,L表示光线在流场中的传输距离[18].

利用基于(3)式获取的OPD直接计算的均方根植OPDrms作为标准结果,并将其与基于密度脉动在光线传播方向上互相关结果积分((6)式)获取的结果进行对比,这里选取光线入射角α=90°,互相关计算参考点x坐标选取为孔径中心处,计算结果如图9所示.

在光束入射角度α=90°时,直接计算结果与基本方程计算结果符合得很好.从基本方程可知气动光学效应主要与光线在边界层内传输的距离以及沿光线传输方向密度脉动的互相关结果有关.如上文所述,光线入射角度的改变,明显地改变了光线在边界层内的传输距离,进而对不同入射角度条件下边界层的气动光学效应产生明显影响,这里不再赘述.然而,相对于垂直壁面方向相同偏角的情况下,光线向上游倾斜入射与向下游倾斜入射时光学畸变的差异性只可能通过密度脉动在光线传输路径上的互相关计算结果说明.本文直接在流向平面(x-y平面)对密度脉动进行空间两点相关性计算,以便可以获得任意入射角度(α=0°—180°)下的密度脉动互相关结果,密度脉动空间两点互相关系数可以表示为在此,我们选取互相关计算的流向尺寸和法向尺寸均为边界层厚度δ,并在湍流边界层内法向不同高度处的三个点进行密度脉动空间两点互相关计算,即(0.5δ,0.2δ),(0.5δ,0.5δ),(0.5δ,0.8δ),计算结果如图10所示.

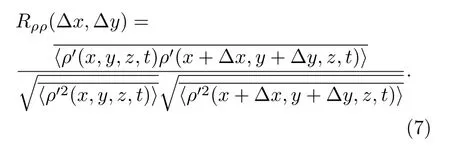
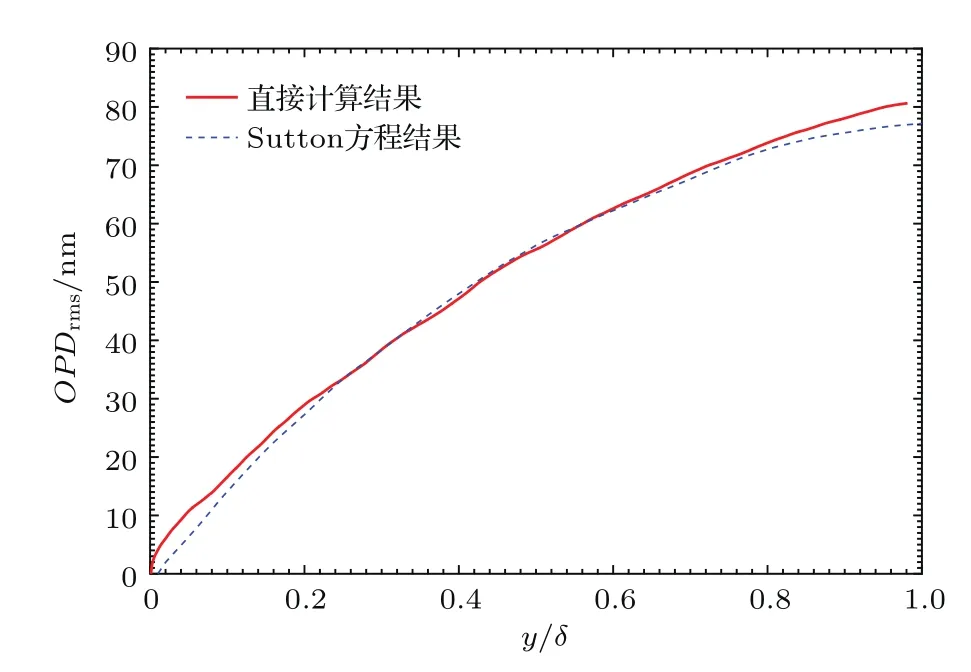
图9 (网刊彩色)直接计算OPDrms与气动光学联系方程计算OPDrms对比Fig.9.(color online)Comparison of OPDrmscalculated by direct integration and aero-optical linking equation.

图10中左图为获得的空间两点互相关系数云图,图10中右图为基于左图中系数Rρρ=0.5的等值线对应的坐标数据,利用最小二乘方法拟合得到的椭圆结果,对应的椭圆参数见表2,其中aside表示拟合椭圆长轴,bside表示拟合椭圆短轴,β表示拟合椭圆长轴与流向夹角,ε表示拟合椭圆偏心率.Smith和Dutton[19]的研究结果表明,利用此拟合椭圆参数可以在一定程度上表征流场中湍流结构的特征参数.

图10 (网刊彩色)不同位置处密度脉动空间两点互相关系数分布图 (左图为Rρρ分布图,右图为Rρρ=0.5等值线及椭圆拟合结果) (a)(0.5δ,0.2δ);(b)(0.5δ,0.5δ);(c)(0.5δ,0.8δ)Fig.10.(color online)Two-point correlations of density fl uctuations at different positions(left,distributions of Rρρ;right,contour line of Rρρ =0.5 and corresponding ellipse fi tting result):(a)(0.5δ,0.2δ);(b)(0.5δ,0.5δ);(c)(0.5δ,0.8δ).

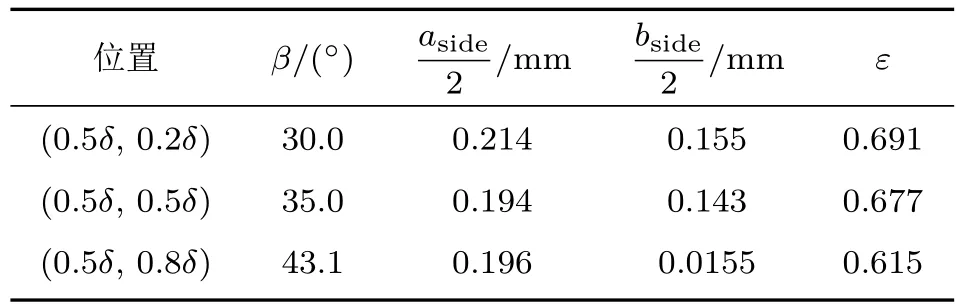
表2 不同位置处Rρρ=0.5等值线对应拟合椭圆参数Table 2.Parameters of fi tting ellipse corresponding to contour line of Rρρ =0.5 at different positions.

根据Smith和Dutton[19]的研究结果,拟合椭圆的长轴与流向的夹角即为当地流场拟序结构的平均倾斜角,半长轴大小表征了当地拟序结构的尺度.拟合椭圆结果表明湍流边界层内从内层到外层三个参考点处拟序结构的平均倾斜角依次为30.0°,35.0°和43.1°,即平均结构倾角沿垂直壁面方向不断增加,这与边界层内发卡涡的发展特点是一致的.当地拟序结构尺度在0.20 mm附近,利用Mani等[20]提出的气动光学有效尺度确定公式计算得到的气动光学效应有效涡尺度最小值约为0.18 mm,与本文采用的互相关方法确定的拟序结构尺度基本一致,这一方面说明了利用空间两点互相关方法可以作为可靠的光学有效尺度确定方法,另一方面说明了此尺度的涡会对气动光学效应产生明显的影响.与此同时,此尺度的拟序结构具有明显的各向异性特点,导致当光线倾斜向下游入射时,光线与流场中具有特征倾角的长细结构具有较多的一致性,体现为此方向上密度脉动互相关系数值较大,故导致了气动光学畸变的加重.与此相反,光线倾斜向上游入射时,其一致性较小,故气动光学畸变相对较弱.

4 结 论

采用NPLS技术测量了超声速(Ma=3.0)湍流边界层的密度分布,利用光线追迹方法获得OPD信息,对OPD测量结果的有效性进行验证,研究了光线入射角度对于超声速湍流边界层气动光学效应的影响.气动光学效应对光线入射角度的依赖性来自于光线在流场中传输路径的影响,而传输路径导致了光线在流场中传输距离以及对应密度脉动互相关结果的差异.光线倾斜入射导致其在流场中传输距离的增长,这种增长对于气动光学效应的恶化影响很大,使得相对于壁面垂直方向相同偏角下的气动光学效应具有较好的对称性.与此同时,光线入射方向与壁面垂直方向之间的夹角越大,气动光学效应越显著,而且不同时刻的差异性增加,气动光学效应校正的难度增加.超声速湍流边界层中大量具有特定方向的涡结构导致了湍流边界层气动光学效应的各向异性,当光线倾斜向下游入射时,光线传播方向与流场中的涡结构特征方向具有较好的一致性,体现为此方向上密度脉动互相关系数较大,故气动光学效应比较严重.而当光线倾斜向上游入射时,相关系数较小,故气动光学效应较弱.

[1]Guo G M,Liu H,Zhang B 2016Appl.Opt.55 4741

[2]Zhu Y Z,Yi S H,Chen Z,Ge Y,Wang X H,Fu J 2013Acta Phys.Sin.62 084219(in Chinese)[朱杨柱,易仕和,陈植,葛勇,王小虎,付佳2013物理学报62 084219]

[3]Ding H L,Yi S H,Fu J,Wu Y Y,Zhang F,Zhao X H 2017Infrared and Laser Engineering46 0211002(in Chinese)[丁浩林,易仕和,付佳,吴宇阳,张锋,赵鑫海2017红外与激光工程46 0211002]

[4]Liepman H W 1952Tech.Rep.SM-14397

[5]Tromeur E,Garnier E,Sagaut P,Basdevant C 2003J.Turbul.4 1

[6]Tromeur E,Garnier E,Sagaut P,Basdevant C 2006J.Turbul.7 1

[7]Wang K,Wang M 2012J.Fluid Mech.696 122

[8]Wyckham C M,Smits A 2009AIAA J.47 2158

[9]Gordeyev S,Smith A E,Cress J A,Jumper E J 2014J.Fluid Mech.740 214

[10]Jumper E J,Gordeyev S 2017Annu.Rev.Fluid Mech.49 419

[11]Yi S H,Tian L F,Zhao Y X,He L,Chen Z 2010Chin.Sci.Bull.55 3545

[12]Tian L F,Yi S H,ZhaoY X,He L,Cheng Z Y 2009Sci.Chin.Phys.Mech.Astron.52 1357

[13]He L,Yi S H,Lu X G 2017Acta Phys.Sin.66 024701(in Chinese)[何霖,易仕和,陆小革 2017物理学报 66 024701]

[14]Gao Q,Yi S H,Jiang Z F,He L,Zhao Y X 2012Opt.Express20 16494

[15]Gao Q,Yi S H,Jiang Z F,Zhao Y X,Xie W K 2012Chin.Phys.B21 064701

[16]Ding H L,Yi S H,Zhu Y Z,He L 2017Appl.Opt.56 7604

[17]Jones M I,Bender E E 200132nd AIAA Plasmadynamics and Lasers ConferenceAnaheim,USA,June 11–14,2001 p1

[18]Hugo R J,Jumper E J 2000Appl.Opt.39 4392

[19]Smith K M,Dutton J C 2001Phys.Fluids13 2076

[20]Mani A,Wang M,Moin P 2008J.Comput.Phys.227 9008