Non-Kolmogorov湍流大气中小尺度热晕效应线性理论∗

张鹏飞 乔春红 冯晓星 黄童 李南 范承玉 王英俭

(中国科学院安徽光学精密机械研究所,大气成分与光学重点实验室,合肥 230031)

(2017年5月16日收到;2017年7月24日收到修改稿)

1 引 言

高能激光在大气中传输,受到湍流效应及非线性热晕效应的影响,严重限制了激光的传输质量.对于大气湍流效应引起的光束抖动、漂移与扩展,使用自适应光学系统的实时补偿可以明显改善光束质量.然而对于非线性热晕效应的相位补偿,由于存在相位补偿的正反馈机制[1,2],在一定条件下会严重限制自适应光学系统对热晕效应的补偿能力.

当光束直径较小时,整束热晕成为限制非线性热晕效应相位补偿的主要因素;但对于大口径准直光束,当热晕主要集中于近口径位置时,整束热晕效应变得不再明显,媒质中不均匀源造成的光束振幅起伏和相位扰动成为影响高能激光湍流热晕传输的主要因素.扰动在非线性热晕效应的作用下逐渐放大,这种现象称为受激热瑞利散射(STRS)[1,2],在湍流介质中的放大现象也可以称为湍流热晕相互作用(TTBI)[3].当存在自适应光学系统补偿时,由于自适应光学系统与主激光之间的正反馈作用,使得这些扰动增长速率高于TTBI或STRS的增长速率,这种现象称为热晕补偿不稳定性(PCI)[4],这些小尺度扰动的发展程度最终确定了高能激光在大气中的传输效率.

小尺度热晕的研究主要集中于20世纪90年代,小尺度热晕线性理论主要建立于90年代末期,Briggs[5],Karr[3,4,6−8],Chambers[1,2]和Viecelli[1,2]等是主要贡献者.他们进行了大量的数值模拟及对比实验[5,8−11],验证了小尺度热晕线性理论的正确性,但是这些研究主要针对Kolmogorov谱大气湍流.实际的大气湍流不总是符合Kolmogorov谱的[12−15],大量的实验报道了湍流的non-Kolmogorov谱特征.激光在non-Kolmogorov湍流大气中传输特性[16−19]的研究也已有较多的进展,但对于non-Kolmogorov湍流与热晕效应相互作用的研究相对较少.本文对小尺度热晕理论进行了推广,使其能够应用于non-Kolmogorov湍流大气中.

2 理 论

在傍轴近似下,高能激光在大气中的传输方程[1−3]可以表示为

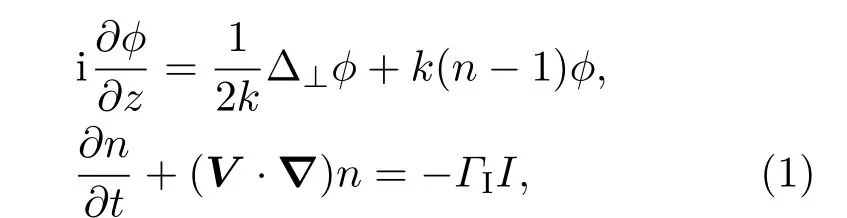
式中ϕ为光场函数,k为波矢,z为纵向坐标,n为折射率,Δ⊥为横向拉普拉斯算符,t为时间变量,I为路径上光强分布,V为大气风速,∇为梯度算符;ΓI=α|nT|/ρCP,α为吸收系数,ρ为空气密度,CP空气的定压比热容,nT为折射率随温度变化率.对方程(1)在拉氏、傅氏域求解可以得到

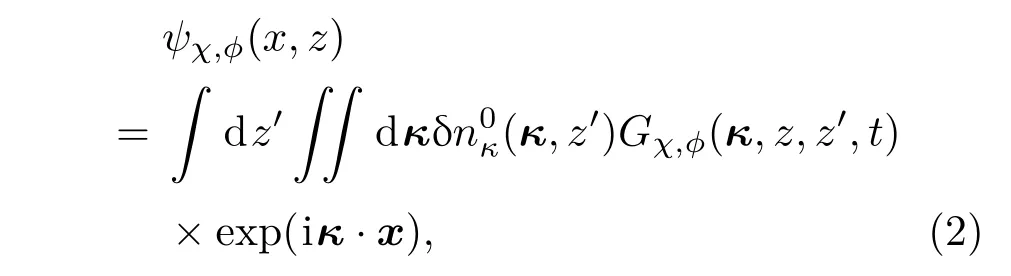
式中x为二维空域坐标,κ为二维频域坐标,表示传输路径上折射率扰动的初始分布,角标χ,ϕ分别对应于对数振幅及相位.对应的时域中对数振幅及相位扰动的格林函数可以表示为[3,4,20−25]

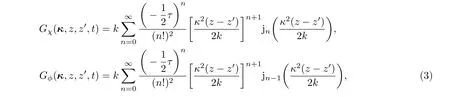
式中,τ=4k2ΓII0t/κ2,jn为n阶球贝塞尔函数.

在自适应光学系统闭环条件下,时域中对数振幅及相位扰动的格林函数[20−25]可以写为

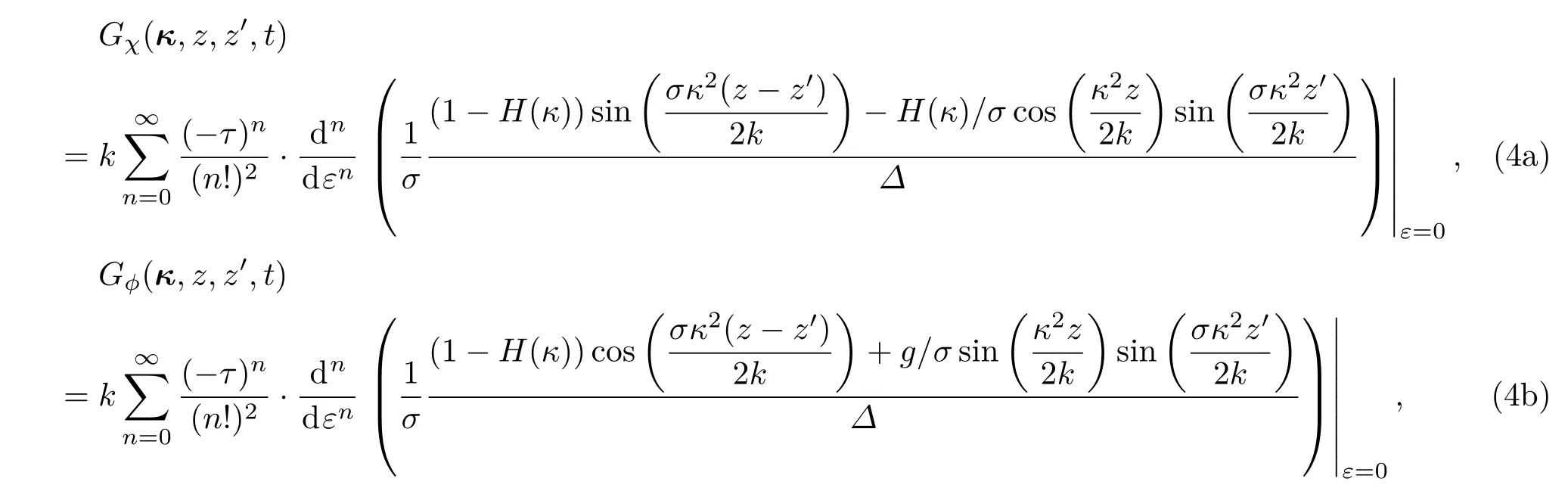
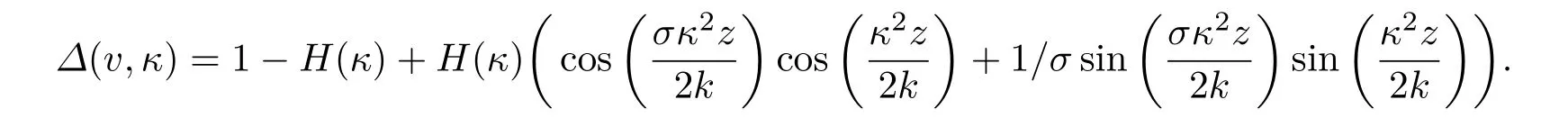
对非均匀路径上TTBI开闭环的格林函数可以通过Wentzel-Kramers-Brillouin[4]近似进行推广.利用自适应光学系统开环及闭环条件下的格林函数,对数振幅起伏及相位起伏的相关函数可以表示为

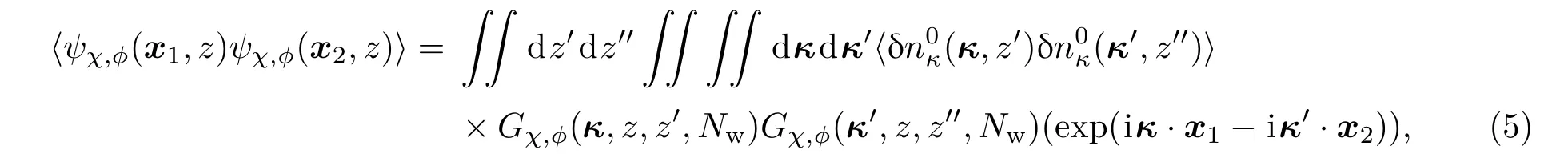
式中Nw=ΓIIkzt为热晕半径,表征一定时间内热晕引起的相位畸变的程度,单位为rad.对于平台光束,稳态时热晕半径Nw与热畸变参数ND的关系为湍流折射率的相关函数可以表示为[26,27]

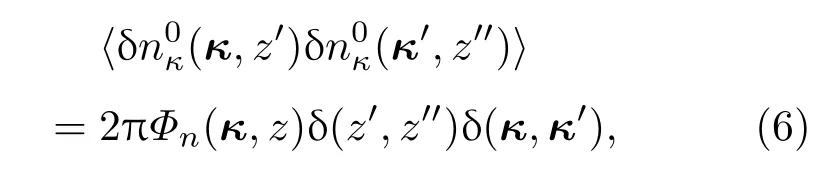
式中Φn为湍流折射率谱函数.将方程(6)代入方程(5),方程(5)可以化简为

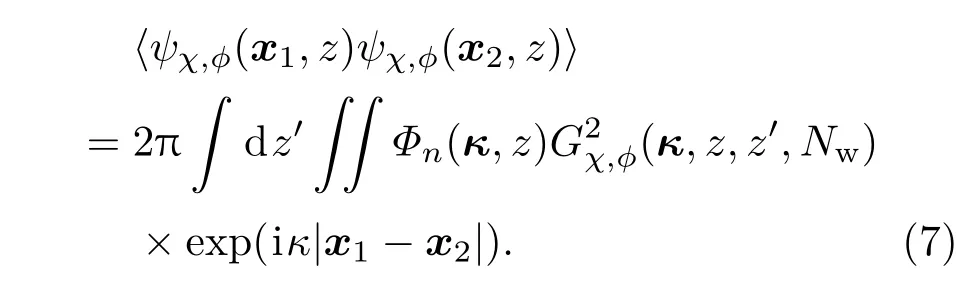
对于non-Kolmogorov湍流,谱函数[28−32]可以推广为一般的形式:

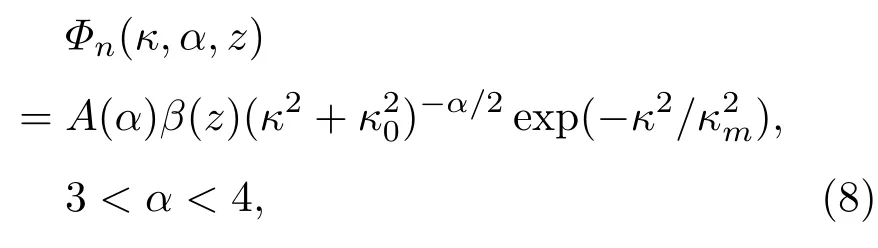
式中A(α)=Γ(α−1)cos(απ/2)/(4π2);β(z)为湍流的广义折射率结构常量,单位为m(3−α);κ0=2π/L0,κm=2π/l0,L0为湍流的外尺度,l0为湍流的内尺度,单位为m;α为湍流谱指数,当谱指数为11/3时对应于Kolmogorov湍流.为计算简便,一般忽略湍流的内外尺度影响.

平面波广义大气相干长度可以表示为[31,32]

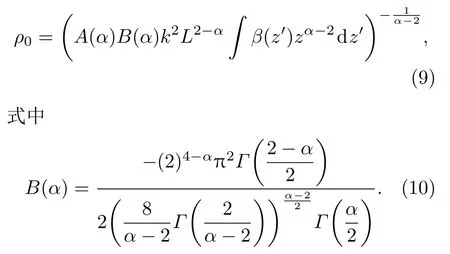
因此在忽略湍流内外尺度的条件下,对数振幅及相位起伏的结构函数可以表示为

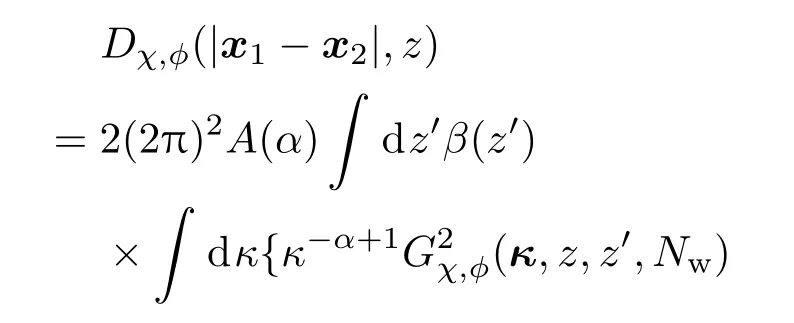
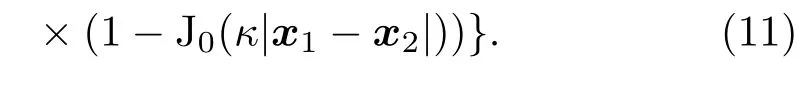
光场的结构函数可以表示为

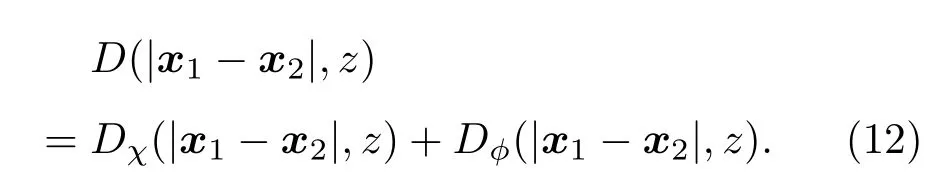
方程(12)是普遍适用的,只要确定了格林函数,那么光场的结构函数便确定了.下面对其分类讨论.

1)纯湍流效应下的结构函数

在仅考虑湍流效应的情况下,方程(3)和(4)可以得到简化,在自适应光学系统开环条件下,

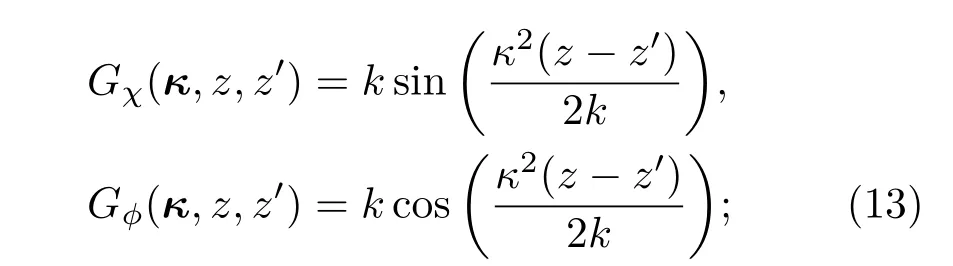
而在自适应光学系统闭环条件下

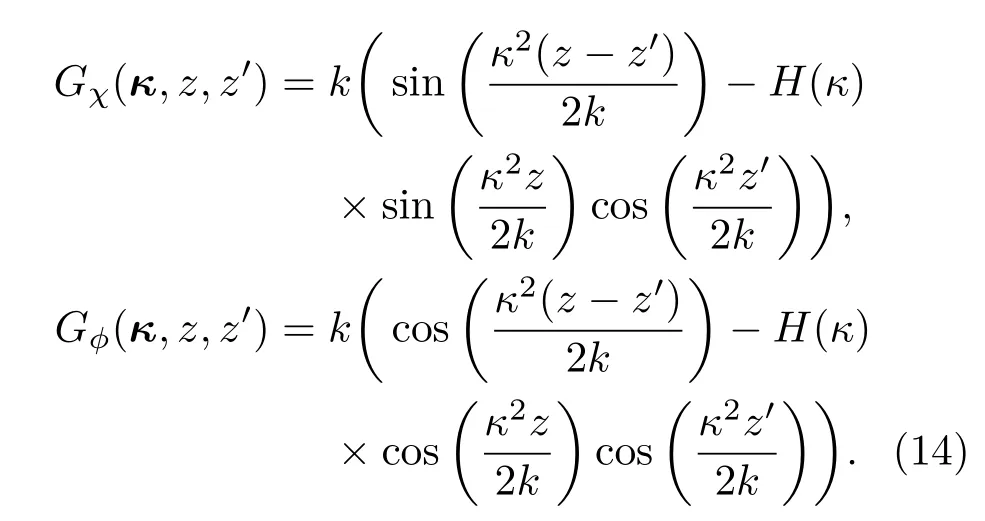
当自适应光学系统开环时,将自适应光学系统开环时的结构函数(13)代入方程(12),对应的结构函数可以表示为

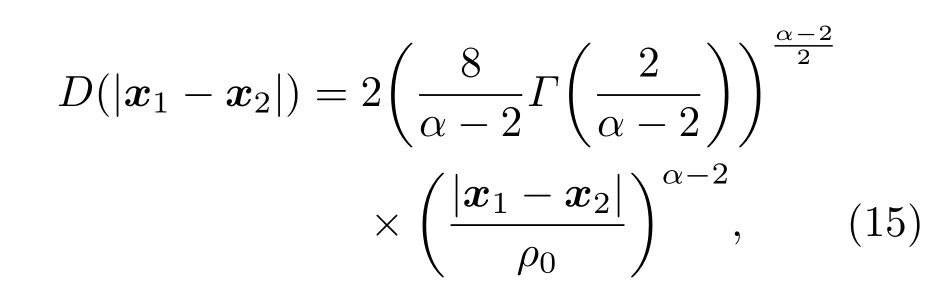
这与文献[31,32]中结构函数计算结果是一致的.

其中D0为发射系统孔径,λ为激光波长,NF为光束菲涅耳数,L为传输路径长度,NT为湍流菲涅耳数,κDM为变形镜的截止频率.一般认为变形镜的截止频率κDM与驱动器间距d之间满足κDM=2π/2d[33,34].通常使用驱动器菲涅耳数来表征小尺度热晕中自适应光学系统扰动源的尺度,其定义为Nd=d2/(λL)[33].

在均匀路径上将(14)式代入(12)式经坐标变换得

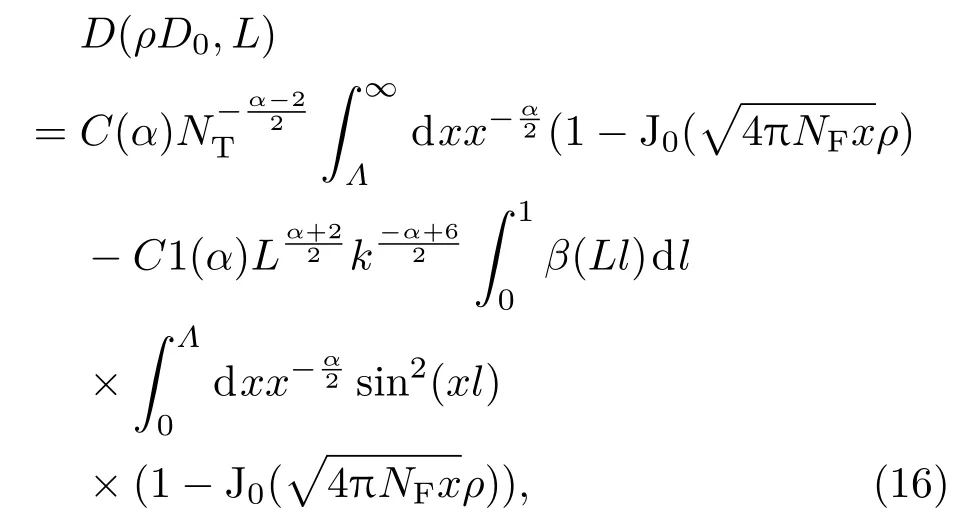
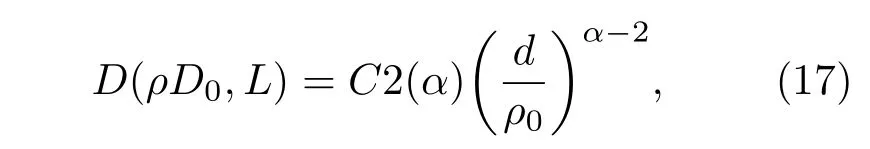
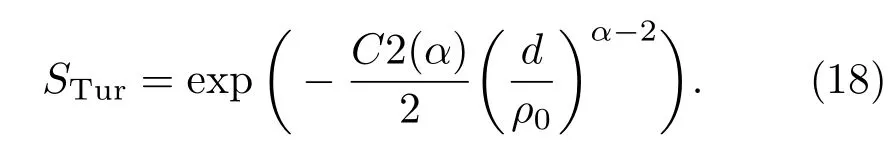
2)湍流热晕效应下的结构函数

同时考虑湍流、热晕效应,在开环条件下,对于大菲涅耳数光束而言,Strehl比会很快趋于0,因此不予考虑.湍流热晕效应闭环时,对数振幅起伏及相位起伏的结构函数可以将补偿的格林函数(4)式代入(12)式进行求解,然而对补偿后结构函数的积分进行数值计算时具有较强的奇异性,数值积分是比较复杂的.Enguehard和Hat fi eld[23,24]指出在驱动器菲涅耳数较大且热晕半径较低时,PCI对光束质量的影响变得不明显,闭环的结构函数可以用开环的格林函数在频率域滤波来实现.此方法容易得到解析的结果,因此,闭环的结构函数可以表示为

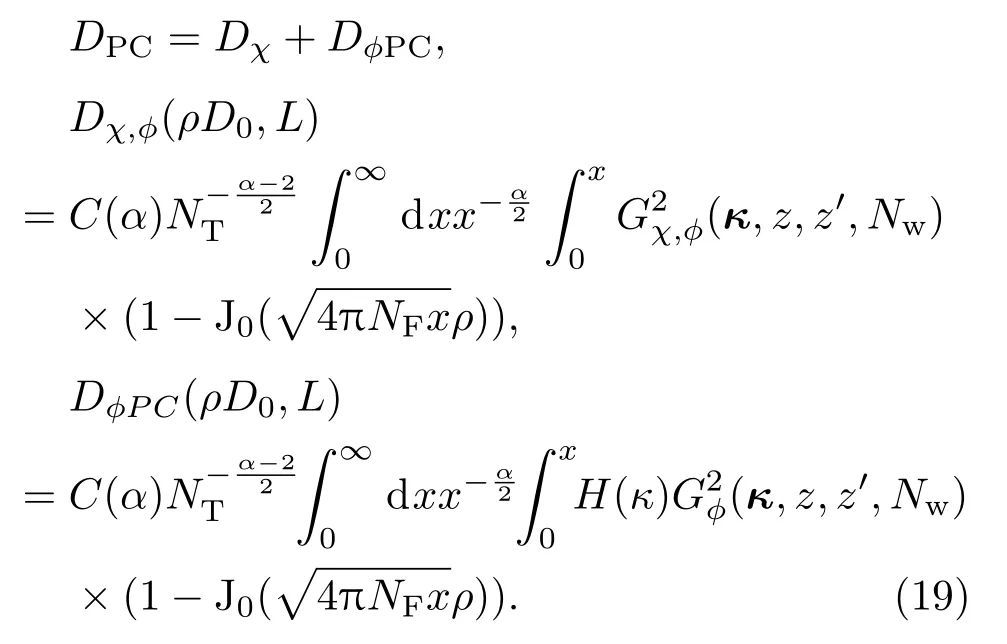
将方程(19)以ε进行Taylor展开,Strehl比可以表示为

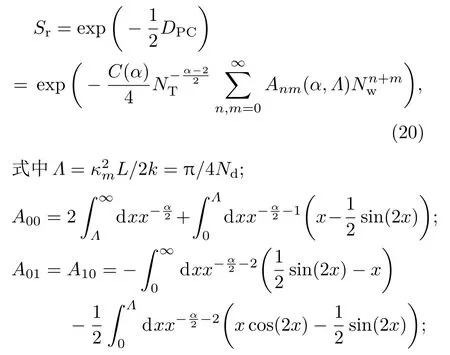
当n+m＞1时,

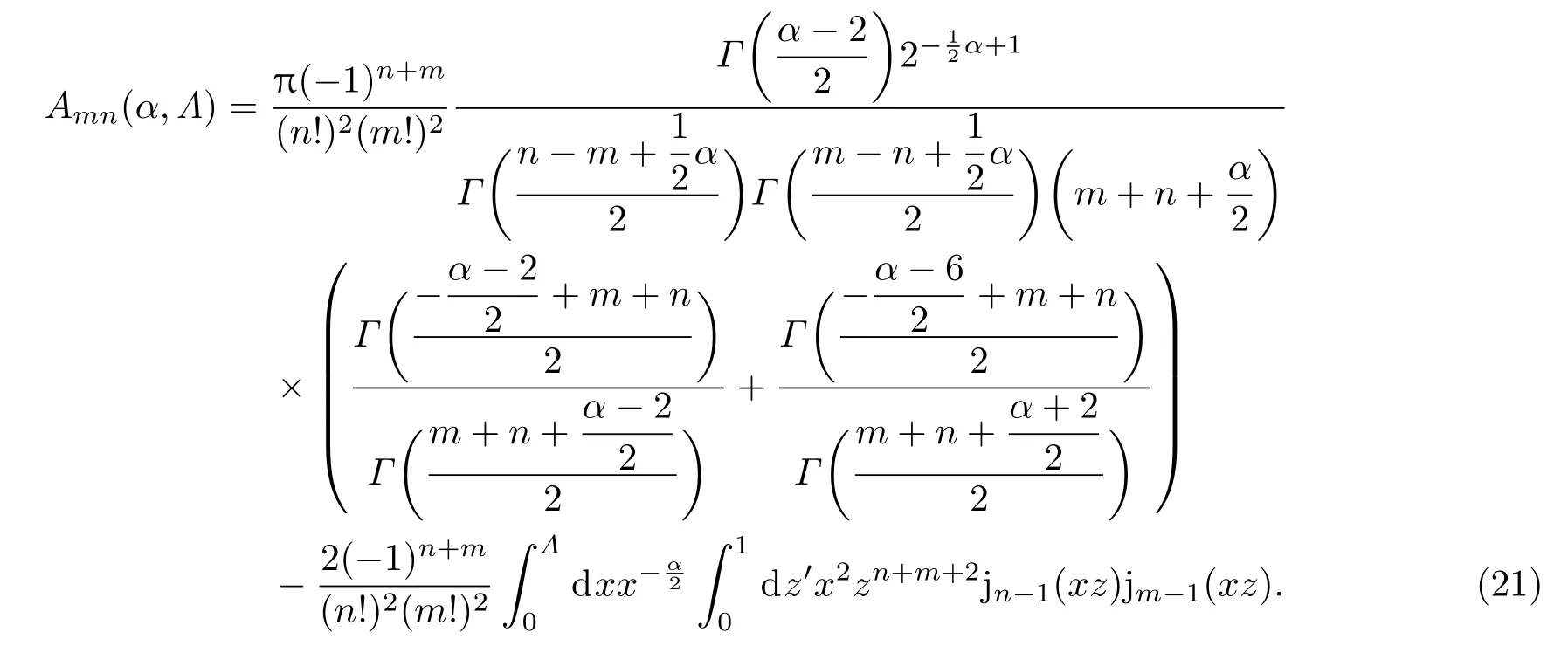
至此,我们得到了平面波non-Kolmogorov湍流下补偿后Strehl比的解析表达式.

Karr[4]指出,小尺度热晕线性理论是可以认为是光在湍流热晕中传输的Rotov近似.因此,与湍流中对数振幅起伏方差做类比,定义湍流热晕中的对数振幅方差为

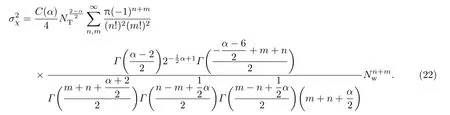
(22)式在忽略热晕效应的影响时,令n=0,m=0,得到

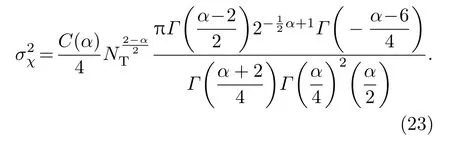
对于Kolmogorov大气湍流,令谱指数α=11/3,(23)式可以化简为σ2χ=0.157N−5/6T.

但是,方程(20)仅为理想的平面波的表达式,对于有限孔径的光束而言,由于风场渡越的作用,结构函数在孔径的不同位置处对应的热晕半径Nw是不同的,因此对光束质量的影响也不同.在上风位置处光束质量较好,而在下风位置处光束质量较差.为了得到有限光束的Strehl比,使用Enguehard和Hat fi eld的方法[21],将光斑分成不同的小块,这些小块等效为不同热晕半径的无限平面波,利用这些小块的Strehl比平均作为有限孔径的Strehl比S,使用数学描述可以表示为

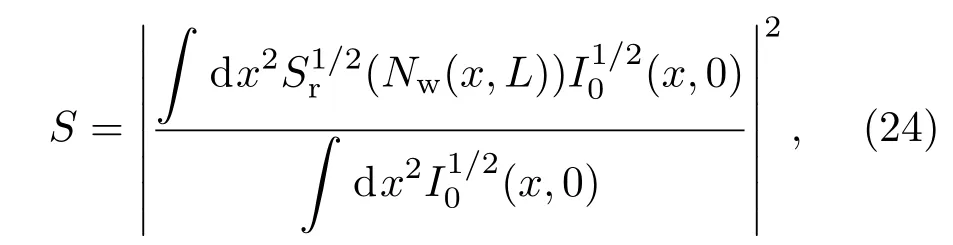
式中Sr为方程(20)计算结果,I0为初始位置处光强分布.

3 湍流谱对热晕补偿的影响分析

图1给出了湍流菲涅耳数NT=20,不同湍流谱指数条件下,方程(24)计算的Strehl比随热畸变参数的变化.计算中主激光使用1.3µm波长,发射口径1.8 m,均匀路径传输2.5 km,驱动器菲涅耳数为2.94和15.74.从图1可以看出:不同湍流谱下,随着热畸变参数的增加,补偿效果逐渐变差;当湍流谱越接近3时,Strehl比下降越快补偿效果越不理想,相反,当湍流谱指数逐渐接近于4时,Strehl比下降越慢,补偿效果越好;在文中条件下,PCI不明显时,使用较小的驱动器菲涅数的自适应光学系统有较好的补偿效果.

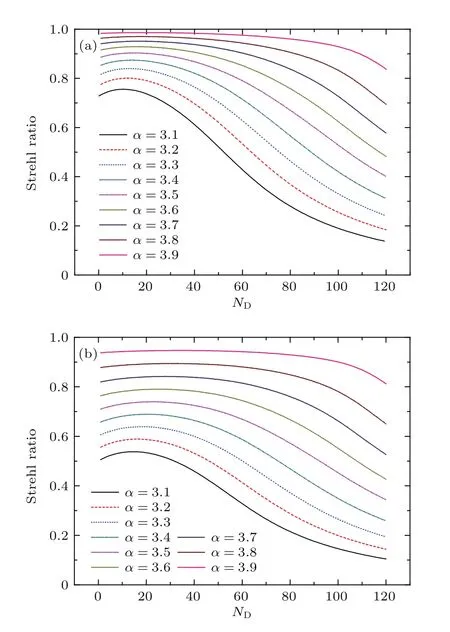
图1 (网刊彩色)相同广义相干长度、不同湍流谱条件下Strehl比随热晕的变化关系 (a)Nd=3.94;(b)Nd=15.74Fig.1.(color online)The relationship between Strehl ratio and thermal distortion number under different turbulence spectrum index with same generalized atmospheric coherence diameter:(a)Nd=3.94;(b)Nd=15.74.

给定β=5.92×10−16m3−α为常量,除湍流强度外使用图1中计算参数,图2给出了不同湍流谱条件下,Strehl比随热畸变参数的关系.从图2可以看出:与图1结果类似,在不同湍流谱下,热畸变参数的增加,补偿效果变差;当湍流谱越接近3时,Strehl比下降越快,当湍流谱指数逐渐接近于4时,Strehl比下降越慢,补偿效果越好;使用较小的驱动器菲涅数的自适应光学系统有较好的补偿效果.但是与图1不同的是在热畸变较弱时自适应光学系统的补偿效果随谱指数有一个先减少后增大的过程,这是由于在β为常量时广义大气相干长度ρ0的非线性变化引起的.

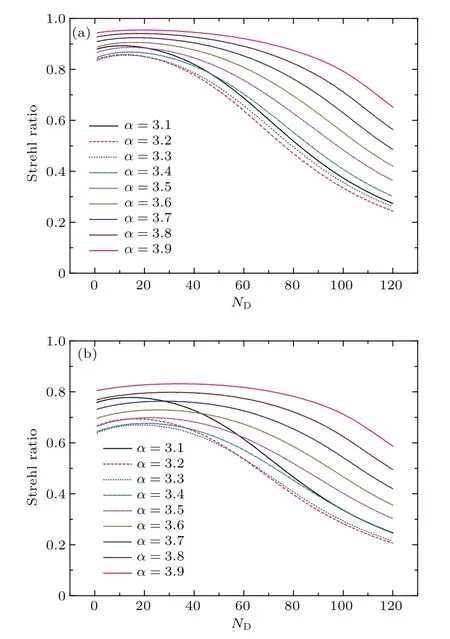
图2 (网刊彩色)相同折射率结构常量、不同湍流谱条件下Strehl比随热晕的变化关系 (a)Nd=3.94;(b)Nd=15.74Fig.2.(color online)The relationship between Strehl ratio and thermal distortion number under different turbulence spectrum index with same generalized index structure constant:(a)Nd=3.94;(b)Nd=15.74.

图3给出了NT=20时,不同谱指数下理想平面波对数振幅起伏方差随热晕的增长情况.从图3可以看出,湍流谱指数越接近3时,对数振幅起伏方差有越快的增长.这是图1、图2计算结果中湍流谱指数由4逐渐接近3时,Strehl比随湍流热畸变增加下降变快的原因.

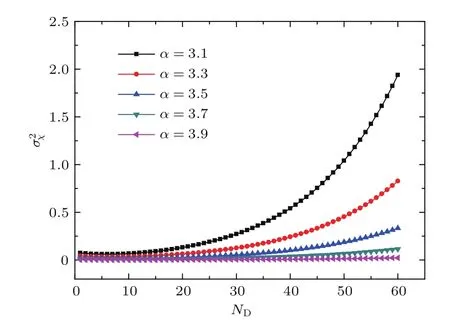
图3 (网刊彩色)NT=20时不同湍流谱条件下对数振幅起伏方差随热畸变参数的变化Fig.3.(color online)NT=20,variation of logarithmic amplitude fl uctuation variance with thermal distortion number under different turbulence conditions.

4 结 论

本文将小尺度热晕理论推广到non-Kolmogorov湍流大气中,对高能激光的实际热晕补偿有重要的理论意义.从小尺度热晕线性理论出发,在non-Kolmogorov谱的基础上,得到了non-Kolmogorov谱湍流下热晕相位补偿的Strehl比表达式,分析了湍流谱对高能激光的相位补偿的影响.湍流谱对湍流热晕效应的相位补偿有重要的影响.在相同的湍流菲涅耳数下,当谱指数越接近于3时补偿效果越差,谱指数接近于4时补偿效果越好;在相同湍流折射率结构常量的条件下,其补偿效果变得复杂.无论在相同大气相干长度条件下,还是在相同湍流折射率常量条件下,当谱指数接近于3时,Strehl比随热晕效应的增强而下降变快,当湍流谱指数逐渐接近于4时,Strehl比下降速度变慢,这是由于随着湍流谱指数的增大,TTBI引起的对数振幅起伏增长变慢而造成的.

[1]Chambers D H,Karr T J,Morris J R,Cramer P,Viecelli J A,Gautesen A K 1990Proc.SPIE1221 83

[2]Chambers D H,Viecelli J A,Karr T J 1990Proc.SPIE1221 220

[3]Karr T J 1990Proc.SPIE1221 26

[4]Karr T J 1989J.Opt.Soc.Am.A6 1038

[5]Briggs R J 1987Lawrence Livermore National Lab.Technical ReportUCID-21118

[6]Karr T J 1991Appl.Opt.30 363

[7]Karr T J,Morris J R,Chambers D H,Viecelli J A,Cramer P G 1990J.Opt.Soc.Am.B7 1103

[8]Karr T J,Rushford M C,Murray J R,Morris J R 1991J.Opt.Soc.Am B8 993

[9]Johnson B,Schonfeld J F 1991Opt.Lett.16 1258

[10]Johnson B,Primmerman C A 1989Opt.Lett.14 639

[11]Higgs C,Fouche D G,Pearson C F 1992Proc.SPIE1628 210

[12]Xue B,Cui L,Xue W,Bai X,Zhou F 2011J.Opt.Soc.Am.A28 912

[13]Cui L Y,Xue B D,Cao X G,Dong J K,Wang J N 2010Opt.Express18 21269

[14]Pérez L D G,Zunino L 2008Opt.Lett.33 572

[15]Tan L,Du W,Ma J,Yu S,Han Q 2010Opt.Express18 451

[16]Shan X,Liu M,Zhang N 2017Opt.Eng.56 026111

[17]Zhou Y,Yuan Y,Qu J,Huang W 2016Opt.Express24 10682

[18]Yan X,Zhang P F,Zhang J H,Qiao C H,Fan C Y 2016Chin.Phys.B25 84204

[19]Huang Y,Wang F,Gao Z,Zhang B 2015Opt.Express23 1088

[20]Wang Y J 1996Ph.D.Dissertation(Hefei:Anhui Institute of Opitcs and Fine Mechanics,Chinese Academy of Sciences)(in Chinese)[王英俭 1996博士学位论文(合肥:中国科学院安徽光学精密机械研究所)]

[21]Enguehard S,Hat fi eld B 2004Proc.SPIE5552 41

[22]Enguehard S,Hat fi eld B 1994J.Opt.Soc.Am.A11 908

[23]Enguehard S,Hat fi eld B 1991Proc.SPIE1408 178

[24]Enguehard S,Hat fi eld B 1991J.Opt.Soc.Am.A8 637

[25]Enguehard S,Hat fi eld B 1991Proc.SPIE1415 128

[26]Andrews L C,Phillips R L 2005Laser Beam Propagation through Random Media(Berllingham:SPIE)pp74–85

[27]Lukin V P,Fortes B V 2002Adaptive Beaming and Imaging in the Turbulence Atmosphere(Berllingham:SPIE)pp15–20

[28]Toselli I,Andrews L C,Phillips R L,Ferrero V 2007Proc.SPIE6551 65510E

[29]Tang H,Ou B,Luo B,Guo H,Dang A 2011J.Opt.Soc.Am.A28 1016

[30]Zhou P,Ma Y,Wang X,Zhao H,Liu Z 2010Opt.Lett.35 1043

[31]Beland R R 1995Proc.SPIE2375 6

[32]Stribling B E,Welsh B M,Roggemann M C 1995Proc.SPIE2471 181

[33]Enguehard S,Hat fi eld B 1995Prog.Quant.Electron.19 239

[34]Tyson R K 1982Appl.Opt.21 787