放射源152Eu的能谱识别及和峰特性分析

许 旭，刘佳强，陆景彬，刘玉敏，赵 龙,，张 伟，龚亚林，马克岩，杨 东，刘运祚

(1.吉林大学 物理学院，吉林 长春 130012； 2.丹东东方测控技术股份有限公司，辽宁 丹东 118002)

152Eu γ源为常用的标准源之一，γ射线数量多，不同能量γ射线132条[1]，能量范围广(121～1 530 keV)，在核物理实验中广泛用于高纯锗探测器的能量刻度和效率刻度。在152Eu γ能谱实际测量中，通常只关心能量刻度和效率刻度的峰而忽略能谱中其他峰，导致有些峰未能说明来源。有研究分别用高纯锗(HPGe)或NaI探测器测量152Eu能谱，在能量为80 keV的位置发现一个较明显的峰，但均未给出解释[2-4]。

测量中发现152Eu源距离高纯锗探头足够近时，能谱中出现了大量和峰，和峰效应会使能谱变杂，降低相关全能峰的有效计数，造成效率刻度不准确。在高自旋实验中，通常使用152Eu源对高纯锗探测阵列进行效率刻度，如果源与探头距离过近，和峰现象明显，会造成效率刻度曲线偏低，影响后续实验γ射线的相对强度以及跃迁多极性等信息的获取。

本研究拟测量放射源152Eu能谱，识别全谱中出现的所有峰，判断出干扰峰；分析和峰的特性，通过计数率和分辨率比较和峰与特征峰的差异，为和峰辨别提供依据；对全能峰计数率进行符合相加修正后，计算源的活度和杂质含量，拟为核谱学相关研究提供参考。

1 实验材料

1.1 实验装置

采用ORTEC公司的GEM-MX5970P4 P型同轴高纯锗探测器，晶体大小为59 mm×70 mm，能量响应范围40 keV～3 MeV，122 keV处半宽度0.9 keV，峰康比62∶1，相对效率38%。

1.2 标准源152Eu

低本底铅室环境，标准源152Eu的出厂活度为6.179×104Bq，出厂时间2006年10月10日，实验日期2015年11月15日。

2 实验方法

2.1 152Eu衰变

152Eu的半衰期为13.522 a，通过轨道电子俘获(72.2%)或β+衰变(0.027%)生成152Sm，β-衰变(27.8%)生成152Gd[5]。152Eu的简化衰变纲图[6]示于图1。

2.2 能谱识别

分别测量源与探头距离为0～9 cm下标准源152Eu的能谱，测量时间均为3 600 s。γ能谱中峰的性质主要取决于[8]：1) 放射源的特征γ射线和分支比，不同能量γ射线的γ能谱特征不同，低能区主要是光电峰，包括锗/碘逃逸峰，中等能量区除光电峰外还有康普顿坪，1.5 MeV以上高能量区域出现单逃逸峰和双逃逸峰；2) 放射源的特性，比如特征X射线及β射线，级联辐射等；3) 探测器的物理性质，包括探测器类型、晶体大小形状、能量分辨率等；4) 实验室条件和环境布置，即屏蔽物、周围物质、与源的距离、计数率高低等。

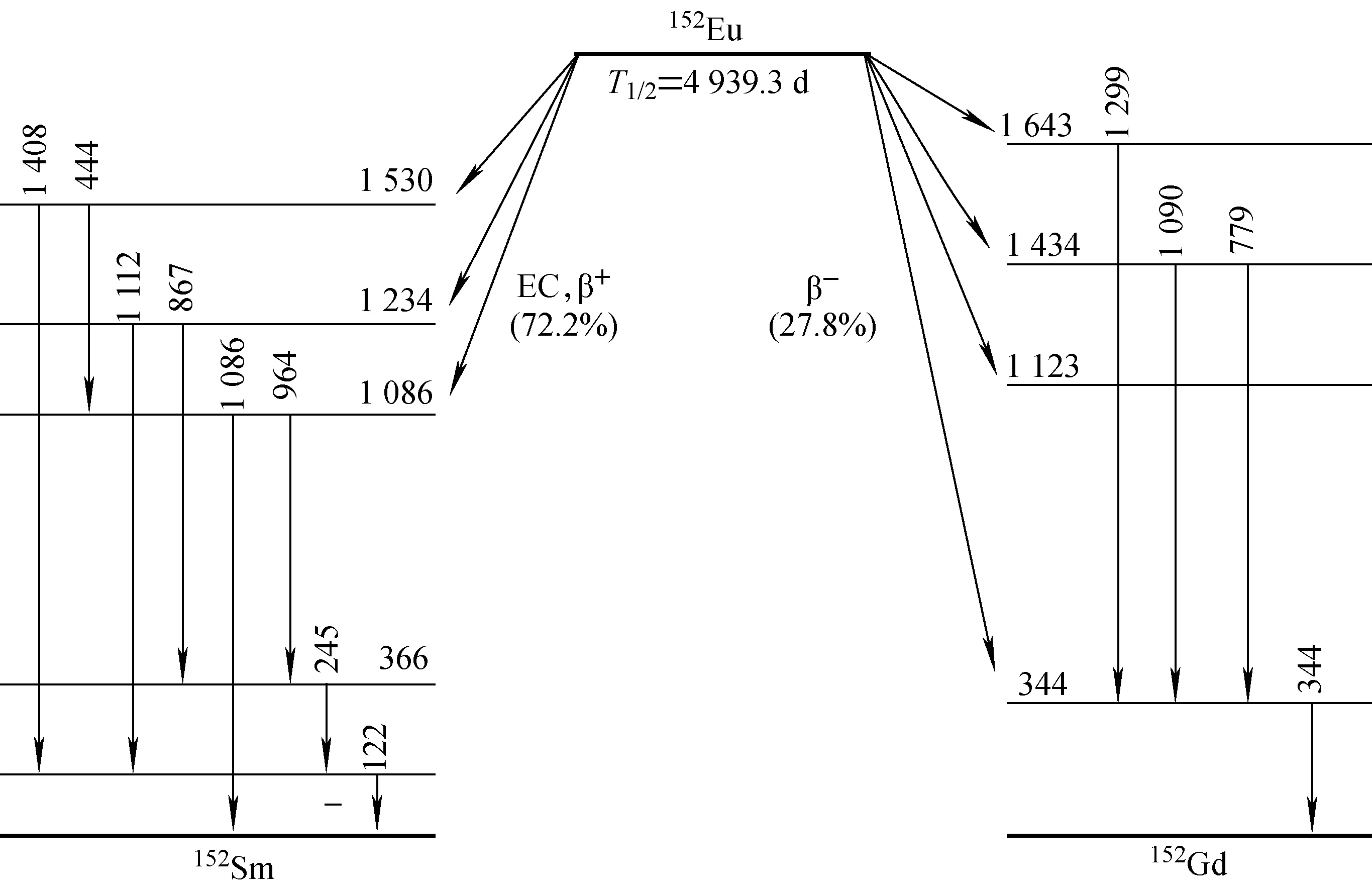
图1 152Eu的简化衰变纲图[6]Fig.1 Simplified decay scheme of 152Eu

2.3 和峰特性

2.3.1计数率随源距的变化

探测器对特征γ射线的计数率为：

n=AIΩε

(1)

式中，A为放射源的活度，Bq；I为γ跃迁的分支比；Ω为探测器对源的立体角；ε为探测器对特征γ射线的全能峰探测效率。根据符合公式[8]，若忽略偶然符合和角关联，不考虑内转换，对于二重符合，级联射线进入同一个探测器时，其立体角Ω是相同的，故符合计数率为：

nc0=AIΩ2ε1ε2

(2)

对于三重符合，符合计数率为：

nc0=AIΩ3ε1ε2ε3

(3)

特征峰、二重和峰、三重和峰的计数率分别正比于Ω、Ω2、Ω3，根据立体角的定义：

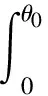
(4)

2.3.2能量分辨率与特征峰的比较

半导体探测器能量分辨率主要由入射射线在晶体中产生电子/空穴对数目的统计涨落(ΔEd)、载流子收集效率的统计涨落(ΔEc)、探测器及电子学系统的噪声(ΔEn)决定[9]。总的能量分辨率半高宽：

(5)

ΔE2=(ΔE)2=2.362FEω+kE+(ΔEn)2=

(6)

若和峰E0=E1+E2，由统计学定理可知，和峰的半高宽为：

(ΔE0)2=(ΔE1)2+(ΔE2)2=(2.362Fω+k)

(7)

(8)

理论上半导体探测器中和峰的能量分辨率比特征峰差，且差异随和峰能量的增大而减小。

2.4 放射源活度及放射性纯度

2.4.1放射源活度

通过和峰及其相关的全能峰计数率计算放射源活度，设两条级联射线的计数率分别为n1和n2，则：

n1=Aε1ΩI1

(9)

n2=Aε2ΩI2

(10)

式中，A为放射源活度；ε1和ε2分别为探测器在射线对应能量的探测效率；Ω为源与探测器的立体角；I1和I2分别为两条射线的绝对强度。设n1为较高能级退激产生的射线的计数率，n2为n1对应射线产生后再次退激产生的射线的计数率。和峰的计数率nc为源活度乘以第一条级联射线的绝对强度，再乘以发生第一次退激后，在该能级再次发生向特定能级退激的概率，即：

(11)

式中，α为内转换系数，能谱中的全能峰计数率实际上损失了发生和峰的计数率，即理论上的全能峰计数率为n+nc，依据式(9)(10)(11)得：

(12)

和峰效应会使全能峰损失一部分计数，但由于一般和峰的计数率比全能峰小两个数量级，在计算中忽略不计。

2.4.2152Eu中154Eu杂质含量计算

已知152Eu活度，利用γ能谱法[11]可以计算154Eu的活度。使用152Eu的 121.78、244.697、344.279、411.117、443.961、586.265、678.623、810.45、867.38、964.057、1 112.07、1 212.948、1 299.142、1 408.01 keV的特征γ射线在源与探头距离为0 cm时进行效率刻度，然后用154Eu特征峰计数率与相应能量位置152Eu的效率刻度做比值，计算154Eu的放射性活度，得到154Eu杂质含量。

3 结果与讨论

3.1 能谱识别

经能量刻度后，源与探头距离d=1 cm时的能谱示于图2。

由图2结果可知，能量为898.19 keV的峰比1 408.08 keV的特征峰能量低约511 keV，推断是1 408.08 keV的单逃逸峰。由于152Eu 1 408.08 keV的特征γ射线与晶体发生电子对效应，正负电子湮灭时产生两个能量为511 keV的湮灭光子，其中一个逃逸出晶体导致。能量为 386.17 keV的峰比1 408.08 keV的特征峰低约1 022 keV，是1 408.08 keV的双逃逸峰。在γ射线能量小于100 keV时光电效应占优势，易形成Ge逃逸峰，30.00 keV 的峰是Sm的X射线(39.9 keV)的Ge逃逸峰。

能量为39.97 keV、45.37 keV的峰为Sm的X射线。轨道电子俘获或内转换均可使核产生X射线。Sm为152Eu轨道电子俘获形成，其X射线既有电子俘获产生的成份又有内转换成份，Gd为152Eu β-衰变产生，其X射线只有内转换成份，所以Gd的X射线(43.0 keV)强度远小于Sm。

能量为723.22 keV、1 274.06 keV的峰，与154Eu的特征γ射线能量对应[7]，能谱中可见与154Eu特征峰能量一致的峰位，如873.40 keV、996.46 keV、1 004.12 keV等 ，峰面积比值与154Eu对应能量特征γ射线强度比值基本一致，表明152Eu 源中含少量154Eu杂质。154Eu为152Eu生产过程中产生的副产物，为中子辐照天然铕元素(47.8% 的151Eu和52.2% 的153Eu)，151Eu俘获中子生成152Eu，153Eu俘获中子生成154Eu。

能量为161.64 keV的峰，杂质元素154Eu中没有能量为161.64 keV的特征γ射线，161.64 keV加上511 keV或1 022 keV均没有对应的特征γ射线，排除为逃逸峰；如果该峰为反散射峰，根据反散射峰公式推出入射γ射线能量应为443 keV，而152Eu没有能量为443 keV的特征γ射线，排除为反散射峰。该峰能量可由121.78 keV的γ射线与39.9 keV Sm的Kα特征X射线相加得到，且121. 78 keV的γ射线与39.9 keV Sm的Kα特征X射线满足级联关系(121.78 keV的γ跃迁在子核152Sm上发生，152Sm由152Eu轨道电子俘获生成，轨道电子俘获伴随X射线的发出，因此X射线与152Sm上的所有γ跃迁都满足级联关系)，推测161.64 keV的峰可能是γ射线与X射线同时被探测器记录，即和峰效应形成。

为了验证猜想，比较不同源距下该峰与244.70 keV的特征γ射线的计数率变化，结果示于图 3。由图3结果可见，161.64 keV和167.37 keV相差约5.7 keV，分别对应121.85 keV与Sm的Kα和Kβ特征X射线加和，即121.85 keV+X(Kα)和121.85 keV+X(Kβ)；随距离的增加，该峰计数率下降比特征峰下降快，在源距较大时峰消失，证明该峰为X-γ 和峰。

同样的方法可以证明与之类似的其他和峰，不同源距下79.76 keV与121.85 keV特征峰计数率的比较示于图4。79.76 keV的X-X和峰(39.9 keV+39.9 keV)，为152Eu通过轨道电子俘获衰变为152Sm并释放出Sm的Kα特征X射线(39.9 keV)，152Sm在退激过程中发生内转换再次释放出Sm的Kα特征X射线，还存在X(Kα)+X(Kβ)和X(Kβ)+X(Kβ)的和峰，为85.41 keV和90.69 keV两个峰的来源，三个峰的计数率随源与探头距离下降的速度快于特征峰。

1 487.9 keV是X-X-γ三重和峰(39.9 keV+39.9 keV+1 408.01 keV)，为152Eu轨道电子俘获衰变到152Sm释放出39.9 keV的Kα特征X射线，152Sm从2-能级退激到2+能级释放出1 408.01 keV的γ射线，2+能级向基态退激时内转换系数高达34.5%[7]，发生内转换后产生39.9 keV的Kα特征X射线。

3.2 和峰特性

3.2.1和峰计数率随源距的变化

实验选取相对强度较大且没有其他干扰的峰，比较不同源距下的净计数率。特征峰(121.85 keV)、二重和峰(161.64 keV)、三重和峰(1 487.90 keV)计数率平均降低倍数和理论计算的比较结果示于图5。由图5结果可见，当源距依次增大时，三种峰的计数率降低倍数不同。特征峰、二重和峰、三重和峰计数率减少速度依次增加，并且实验值与理论计算曲线符合较好。

图2 源与探头距离为1 cm时 152Eu γ能谱Fig.2 Spectrum of 152Eu when d=1 cm

图3 不同源距下161.64 keV与244.70 keV特征峰计数率的比较Fig.3 Comparison of count rate of 161.64 keV and 244.70 keV in different source distance

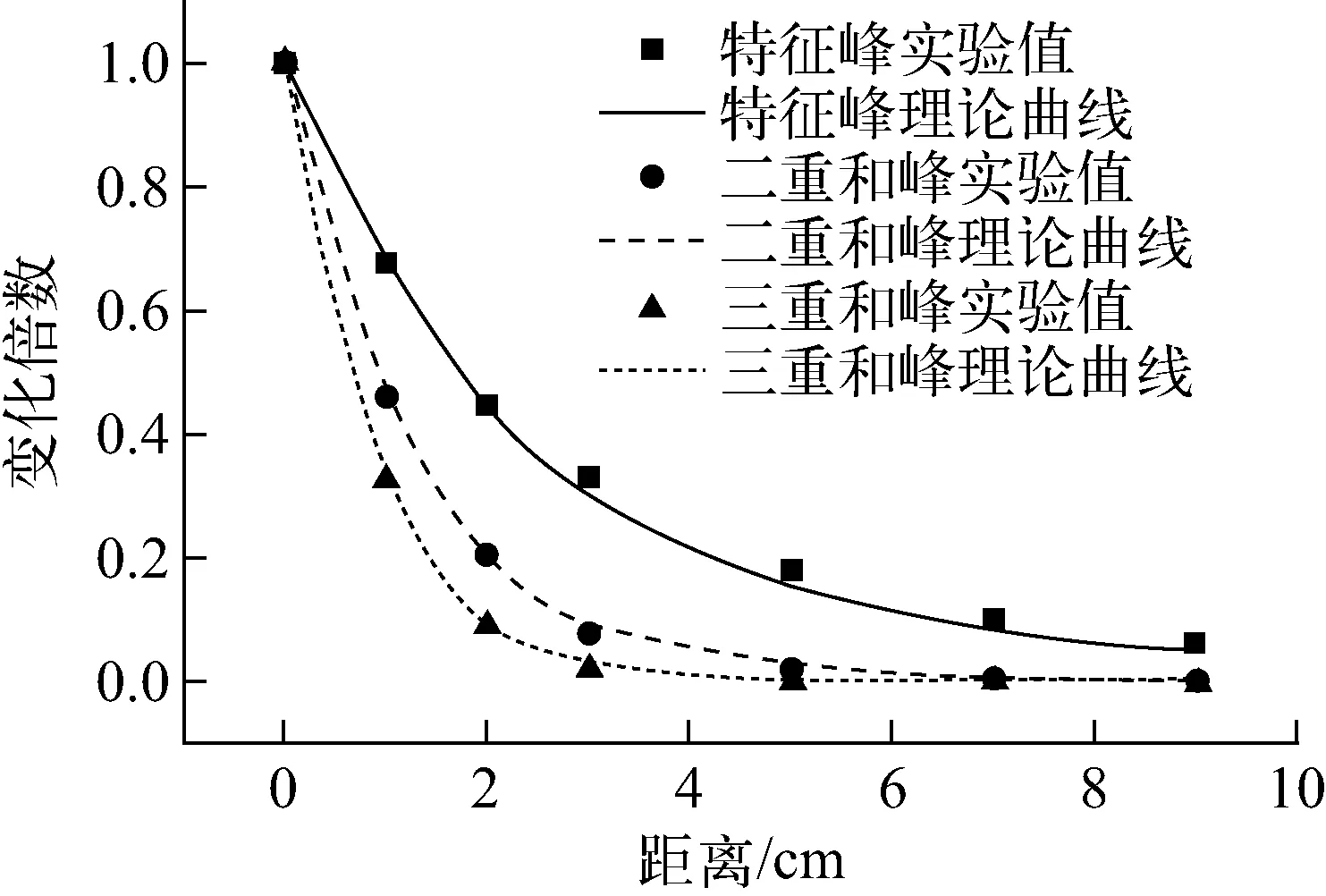
图5 不同源距下特征峰、二重和峰、三重和峰的计数率减少倍数的比较Fig.5 Comparison of counts decrease of characteristic peak, sum peak and triple sum peak in different distance

4.2.2能量分辨率与特征峰的比较

选取相对强度较大且没有其他干扰的峰，作能量分辨曲线示于图6。由图6结果可知， 200 keV时和峰能量分辨率为0.72%，特征峰能量分辨率为0.59%，相差22%，200 keV以下，两者能量分辨率相差更大，随着能量增大，二者能量分辨率差异逐渐减小，因此能量分辨率可作为判断和峰的补充判据。

图6 HPGe探测器中特征峰与和峰能量分辨率对比Fig.6 Comparison of energy resolution of characteristic peak and sumpeak in HPGe

3.3 放射源活度及杂质

3.3.1放射源活度

选取d=0 cm时152Eu能谱中121.85 keV和1 112.12 keV的全能峰及和峰1 233.81 keV，计算峰的净面积。其中，121.85 keV全能峰计数率为(1 565.8±1.41) s-1，1 112.12 keV的全能峰计数率为(103.6±0.39) s-1，1 233.81 keV和峰计数率为(11.7±0.28) s-1，152Eu 中121.85 keV射线绝对强度为28%，内转换系数为34.5%[7]，计算可得152Eu的活度为(36 815±887.9) Bq，根据出厂活度计算出的活度为38 755 Bq，误差为5%；如果考虑和峰计数损失，计算活度为(41 279±995.6) Bq，误差为6.5%。

3.3.2152Eu中154Eu杂质含量

图7 符合相加修正后与未修正的效率刻度曲线对比Fig.7 Comparison of efficiency calibration with summing correction and without correction

源与探头距离为0 cm时高纯锗探测器的效率刻度曲线示于图7。由图7得到121 keV到1.4 MeV效率刻度函数：

lg(ε)=-0.805 5lg(E)+0.327 6

(13)

能量为E的特征峰的计数率为：

n=AIε

(14)

式中，A为放射源活度，I为该射线绝对强度，选取154Eu特征峰1 274.43 keV的计数率为0.441 s-1，绝对强度I=34.8%，计算活度为(196±11.9) Bq，得到154Eu质量为1.96×10-11g。

和峰效应会使本应形成全能峰的γ射线被记录成和峰的计数，使全能峰面积减小，为了进一步说明和峰效应对能谱的影响，将和峰中的计数计入相应级联特征峰内，计算对全能峰符合相加修正后杂质元素的含量，与修正前比较结果列于表 2。修正后的效率刻度函数为：

lg(ε)=-0.801 7lg(E)+0.325 9

(15)

计算得到154Eu放射性活度为(185±11.1) Bq，质量为1.85×10-11g，与未修正相差5.6%。

表2 修正后与未修正的152Eu中154Eu含量计算的对比Table 2 Comparison of 154Eu content in 152Eu with summing correction and without correction

4 小结

1) 采用低本底HPGe探测器测量标准源152Eu的γ能谱，并识别全谱中出现的所有峰，判断出干扰峰包括杂质元素、逃逸峰、和峰等。其中有大部分干扰峰为和峰，包括γ-γ符合、γ-X符合、X-X符合，在源距很近时出现X-γ-γ和X-X-γ的三重和峰。

2) 在单个探测器的测量能谱中，特征峰、二重和峰与三重和峰的计数率分别与Ω、Ω2、Ω3成正比；在HPGe探测器中，能量相同时，和峰的能量分辨率比特征峰差，差异随能量的增大减小。

3) 利用真和峰计数率计算出152Eu的放射性活度为(36 815±887.9) Bq，与出厂活度相差5%，利用γ能谱法计算152Eu标准源中154Eu杂质的活度为(196±11.9) Bq。对全能峰计数率进行符合相加修正，152Eu的活度修正为(41 279±995.6) Bq，与未修正活度相差12.1%；154Eu的活度修正为(185±11.1) Bq，与未修正活度相差5.6%。在高自旋态实验中，如果使用152Eu进行效率刻度，建议源与探测器的距离不小于9 cm，否则应考虑和峰效应导致的全能峰计数损失。

[1] Martin M J. Nuclear data sheets for A=152[J]. Nuclear Data Sheets, 2013, 114(11): 1 497-1 847.

[2] 克劳塞梅尔C E. 应用γ射线能谱学[M]. 高物，伍实，译. 北京：原子能出版社，1977：352-534.

[3] 方晓明. 碘化钠探测器和高纯锗探测器γ能谱仪性能比较[J]. 上海大学学报,2004,10(4):394-392.

Fang Xiaoming. Comparison of performances of NaI and HPGe detectors[J]. Journal of Shanghai University, 2004,10(4): 394-392(in Chinese).

[4] 向清沛. 基于序贯贝叶斯分析的放射性核素快速识别方法研究[D]. 绵阳：中国工程物理研究院，2014.

[5] Dušan N, Mirjana -D. Coincidence summing corrections for point and volume152Eu sources[J].Applied Radiation and Isotopes, 2016, 107: 138-144.

[6] Tae S P, Jong M L, Han Y H. Standardization of152Eu and88Y[J]. Applied Radiation and Isotopes, 2002, 5(1): 275-280.

[7] 刘运祚. 常用放射性核素衰变纲图[M]. 北京:原子能出版社,1982:205-210.

[8] 吴治华. 原子核物理实验方法[M]. 北京:原子能出版社,1997:131-132,264.

[9] Sajo-Bohus L, Rosso D, Castelli A M S, et al. HPGe detectors long time behaviour in high-resolution γ spectrometry[J]. Nuclear Instruments and Methods in Physics Research A, 2011, 648(1): 132-138.

[10] Hurtado S,Garcia-Leon M. A revision of energy and resolution calibration method of Ge detectors[J]. Nuclear Instruments and Methods in Physics Research A, 2006, 564(1): 295-299.

[11] 唐泉，安小刚，丘寿康. 固体219Rn源的γ能谱法放射性纯度检验[J]. 原子能科学技术，2014，48(12)：2 381-2 386.

Tang Quan, An Xiaogang, Qiu Shoukang. Determination of radioactivity purity of solid219Rn source by γ-ray spectrometry[J]. Atomic Energy Science and Technology, 2014, 48(12): 2 381-2 386(in Chinese).