稳态射流数值模拟中速度参量对传热的影响机制分析
张温宇,施能博,孙志新,林 立,许巧玲
(福州大学石油化工学院,福建 福州 350116)
0 引言
射流冲击的工程应用非常广泛,如静叶端壁的冲击冷却,皮革在烘箱内的冲击干燥等. 正是由于其重要的理论研究价值及广泛的工程应用背景,在过去的十几年中,国内外研究学者对射流冲击的流动传热特征开展了大量的实验与数值模拟工作.
Zuckerman等[1]在2006年对冲击传热的理论研究、实验研究和数值模拟做了综述,指出诸多湍流模型中,综合考虑计算量和滞止区传热模拟精度,Transition SST和V2-f模型是值得推荐的. 相比TransitionSST模型,V2-f模型的应用没有得到广泛推广,主要原因在于V2-f湍流模型通常需要更多的迭代次数才能收敛[2],部分工况下甚至难以获得收敛解,因而仍有研究者对V2-f模型进行改进[3]. Hoffmann等[4]对稳态和脉冲冲击射流的数值模拟考察了13种湍流模型的效果,结果表明Transition-SST模型能较好地模拟转捩区域,而其余模型仅在壁面射流湍流区域表现较好. 也有不少研究表明,RNGk-ε模型在射流冲击模拟中具有较好的适用性,例如,Isman等[5]考察了5种湍流模型对等热流边界下冲击换热的模拟,结果表明RNGk-ε模型和标准k-ε模型对整体换热的预测效果较好; Sharif等[6]对射流冲击平面和柱面实验的数值模拟结果表明,RNGk-ε和Transition SST模型均能较好地模拟射流冲击靶面的流场及壁面换热特性.
纵观国内外研究者关于稳态冲击射流数值模拟的研究可知,RNGk-ε模型和Transition SST模型在该问题上获得了普遍认可,但就具体工况而言,二者的结果还存在明显差异,研究拟通过对文献中的若干实验工况进行数值模拟,考察两个湍流模型的表现,及其在不同工况下的表现,为根据工况优选湍流模型提供更多依据.
1 槽缝射流的物理模型
研究数值模拟所用的两个物理模型如图1所示,具有一定温度和速度的理想气体从二维狭缝中喷出, 进入自由空间或冲击到光滑平板上,而后从出口流出. 狭缝宽度为b,狭缝出口与靶面间的距离为h,其中结构(a)来自文献[7-8],结构(b)来自文献[9]. 考虑了狭缝上游收缩段的影响,两种结构的坐标原点均设置在狭缝出口中点,x和y轴的正方向如图所示.
图1同时给出了数值模拟的边界条件设置情况,其中槽缝入口给定流量(采用均一速度分布),入口静温298 K,入口湍流度为1.5%,对于图1(a)和(b)两种几何模型,槽缝出口的边界层均已充分发展. 出口给定静压为0.1 MPa. 对于自由射流工况,靶面亦为出口,对于冲击射流工况,靶面给定壁温. 各工况具体的几何参数及边界条件参见表1. 大部分为文献中的实验工况,以便和实验结果进行对比.
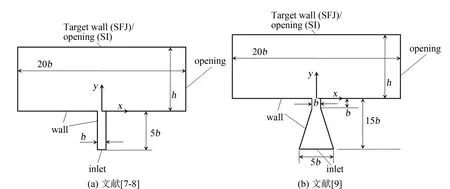
图1 数值模拟几何结构示意图Fig.1 Geometric model of numerical simulations
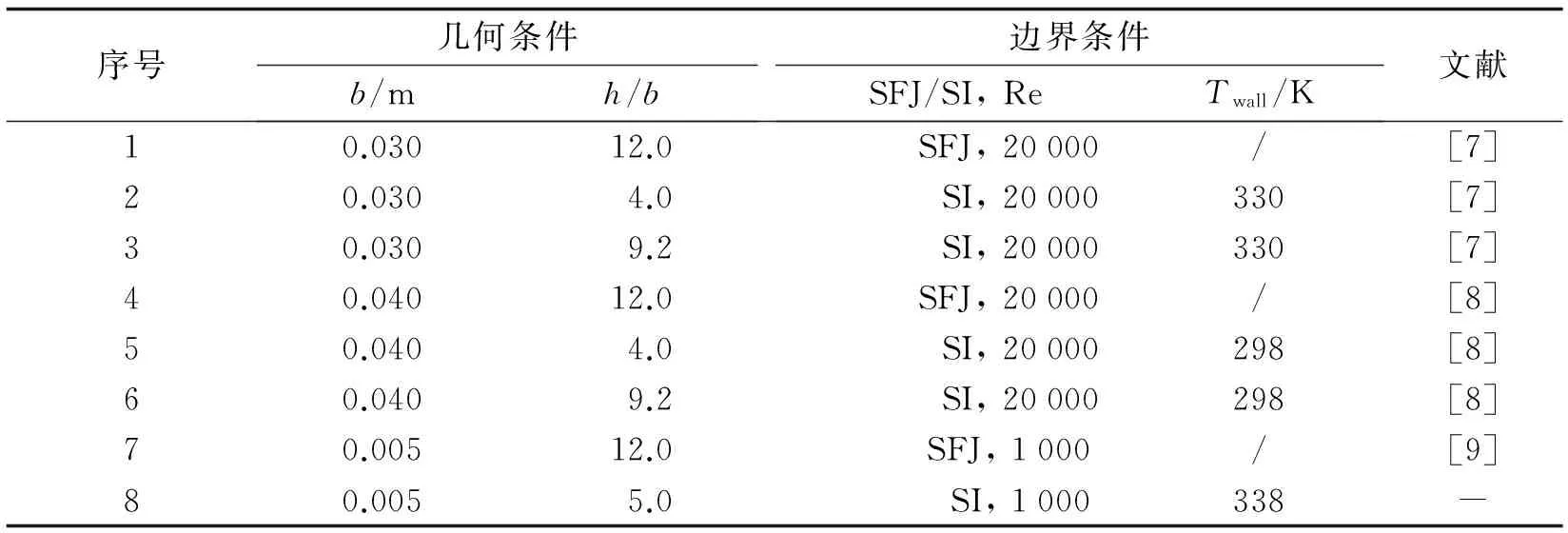
序号几何条件b/mh/b边界条件SFJ/SI,ReTwall/K文献10.03012.0 SFJ,20000/[7]20.0304.0 SI,20000330[7]30.0309.2 SI,20000330[7]40.04012.0 SFJ,20000/[8]50.0404.0 SI,20000298[8]60.0409.2 SI,20000298[8]70.00512.0 SFJ,1000/[9]80.0055.0 SI,1000338-
注:SFJ表示steady free jet, SI表示steady impingement
2 数学模型及计算方法
2.1 数学模型
计算流体动力学(computational fluid dynamics,CFD)技术对于物理问题的描述是基于流体力学的基本控制方程,即连续性方程、动量方程和能量方程,分别对应质量守恒、动量守恒和能量守恒3大物理定律. 对于湍流的数值模拟多是通过求解雷诺平均的控制方程来实现,即RANS(Reynolds average navier-stokes equations)方法. 非定常雷诺平均方程如式(1)~(3)所示.
Re-normalisation groupk-ε(以下简称RNGk-ε)模型[10]:基于对Navier-Stokes 方程的重整化群分析方法,其关于湍流动能和湍动能耗散项的输运方程和标准k-ε模型是相同的,但方程中的系数不同,相比于标准k-ε模型对于强剪切流、漩涡流动有更高精度.
Transition-shear stress transport(以下简称SST)模型:对于湍流模拟,在近壁边界层区域求解k-ω输运方程,而在主流中求解k-ε方程,这样既可以发挥k-ω在求解近壁流动方面的能力,同时又避免主流对ω值过于敏感的问题. 为了实现方程的一致性,将主流中的k-ε方程转化为k-ω方程的形式,另外为了弥补涡粘性模型在对雷诺应力输运效果上的不足,SST 模型引入了关于湍流剪应力输运效果的修正.
对于转捩的模拟,转捩模型采用的是Menter提出的γ-Reθ模型. 其中γ是间歇因子,Reθ是转捩动量厚度雷诺数. 该模型在主流中通过经验关联式计算转捩动量厚度雷诺数,通过输运方程使其扩散到边界层内,以判断是否触发转捩[11].
2.2 计算方法
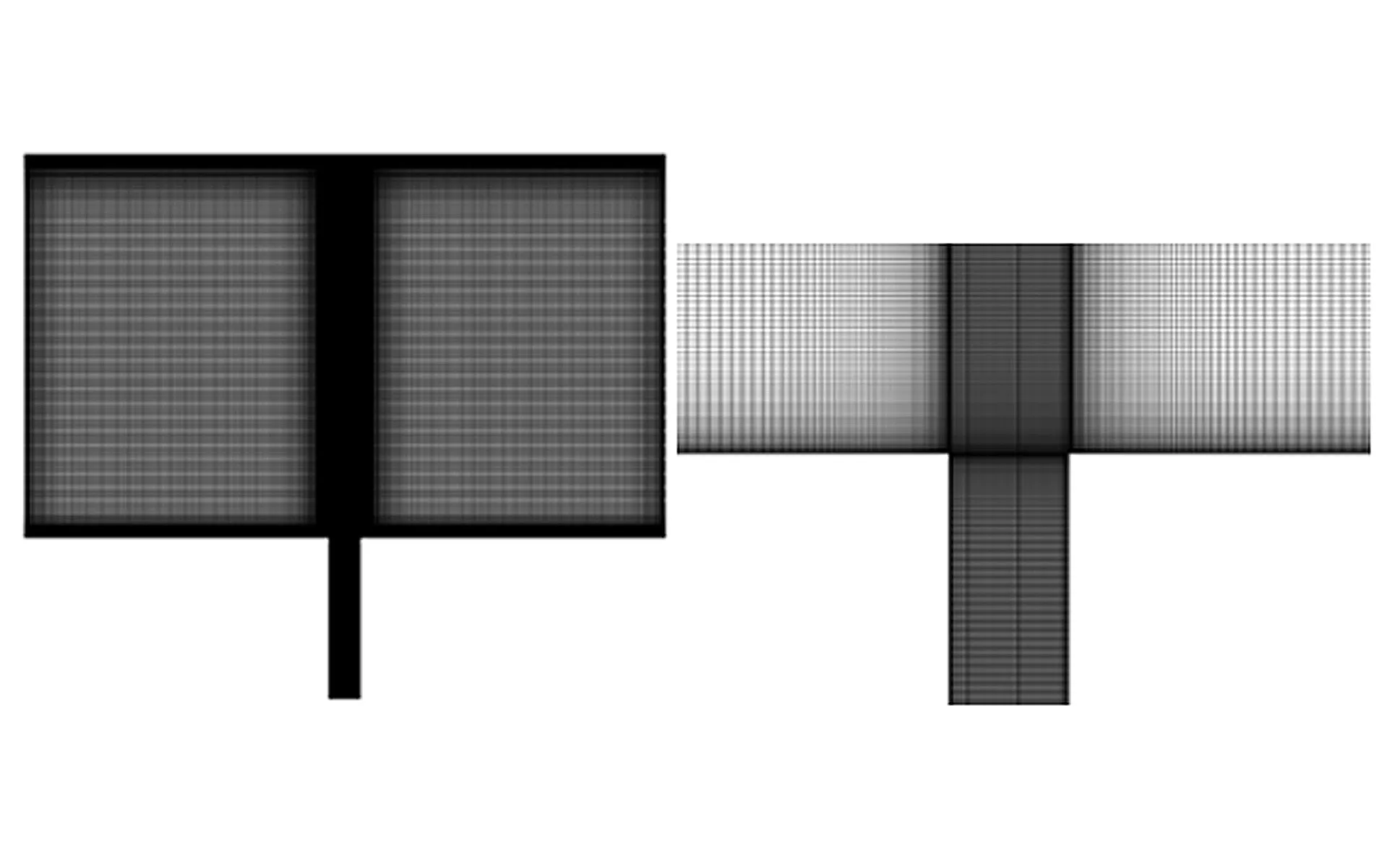
图2 网格示意图Fig.2 Mesh of numerical models
数值模拟采用商业软件Fluent 16.0进行. 采用四边形结构网格,网格划分如图2所示,在射流区域和壁面附近进行加密,保证y+<1,根据网格无关性验证结果,最终确定各工况网格总数为:工况1~3约15万,工况4~6约17万,工况7~8约11万. 采用压力-速度耦合,SIMPLE(semi-implicit method for pressure linked equations)算法进行求解, 控制方程中的对流项,动量方程和能量方程采用二阶迎风格式离散,湍流模型项一律采用一阶迎风格式,扩散项梯度计算采用基于单元体的最小二乘法插值. 收敛判据为能量方程残差绝对值小于10-8,其它所有变量的残差绝对值小于10-4,并监测射流轴线上若干点的速度变化情况,判定流动是否稳定.
3 结果与分析
3组实验结果的最大测量误差如表2所示. 其中(-)表示原始文献未提供相关误差说明,后文数据分析的图中亦标明了相关的误差线. 尽管文献[7-9]中实验设计已尽可能构造二维槽缝射流的流场,但仍不可避免具有一定的三维效应,这也是导致二维数值模拟结果和实验存在偏差的一个重要原因. 下面分别对自由射流和冲击射流的模拟结果进行分析.

表2 各文献实验结果最大测量误差
3.1 稳态自由射流
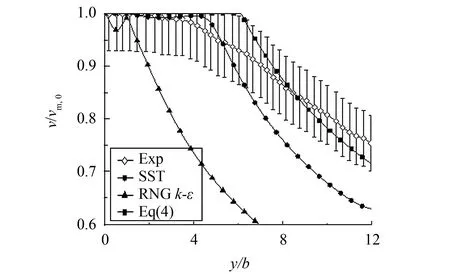
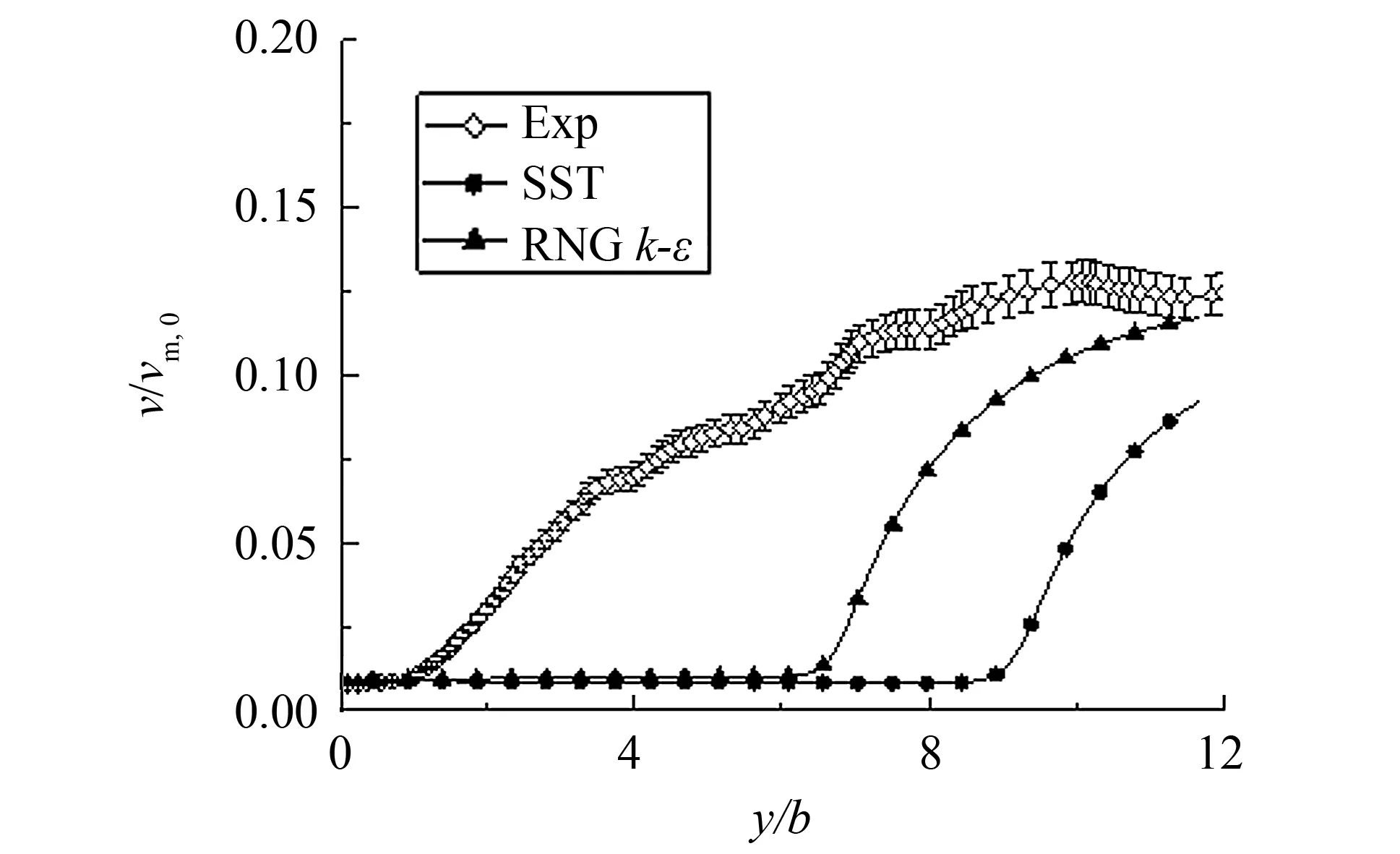
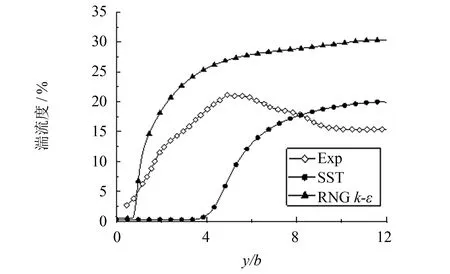
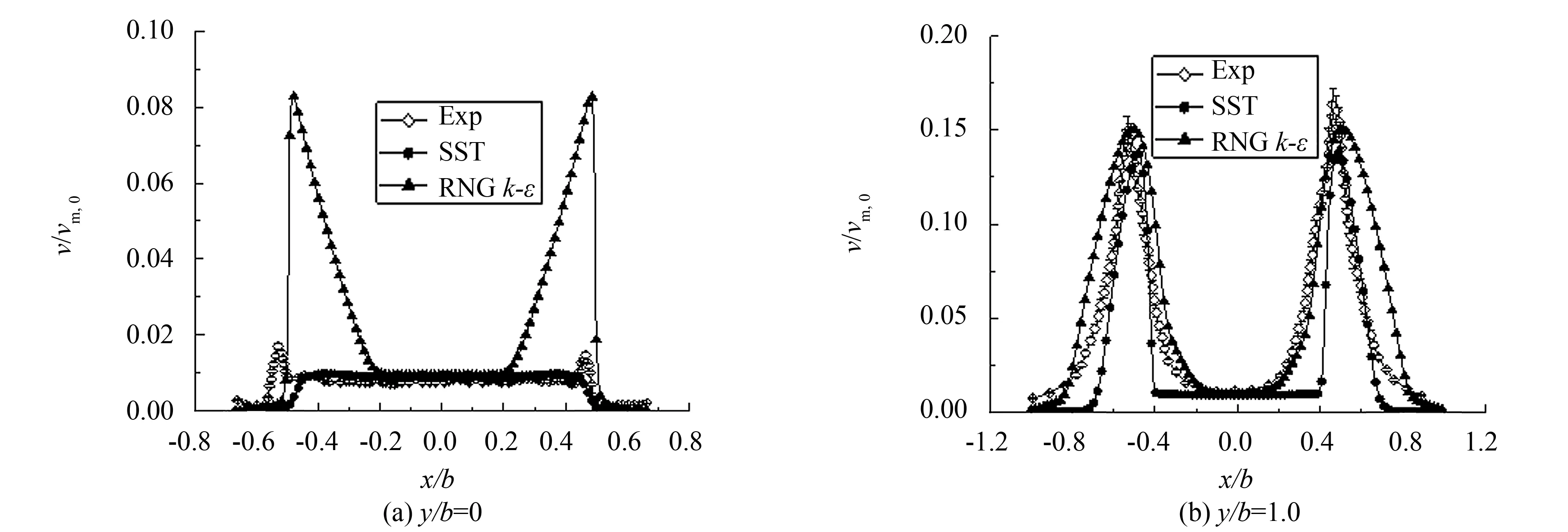
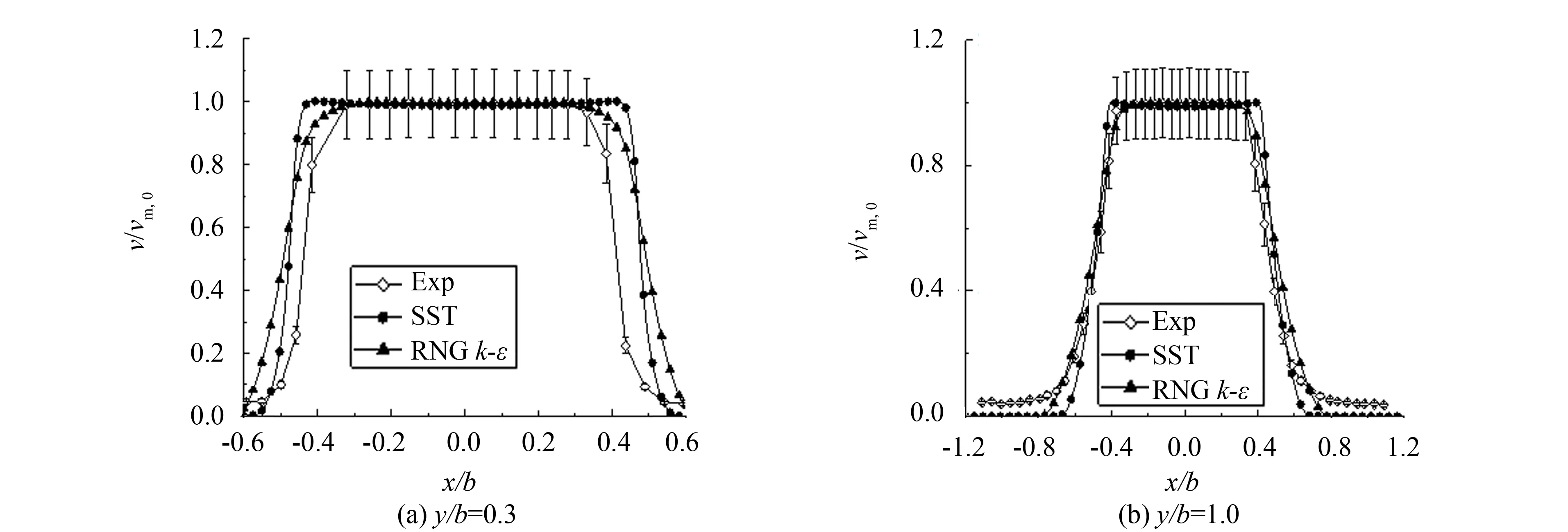
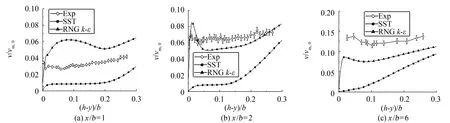
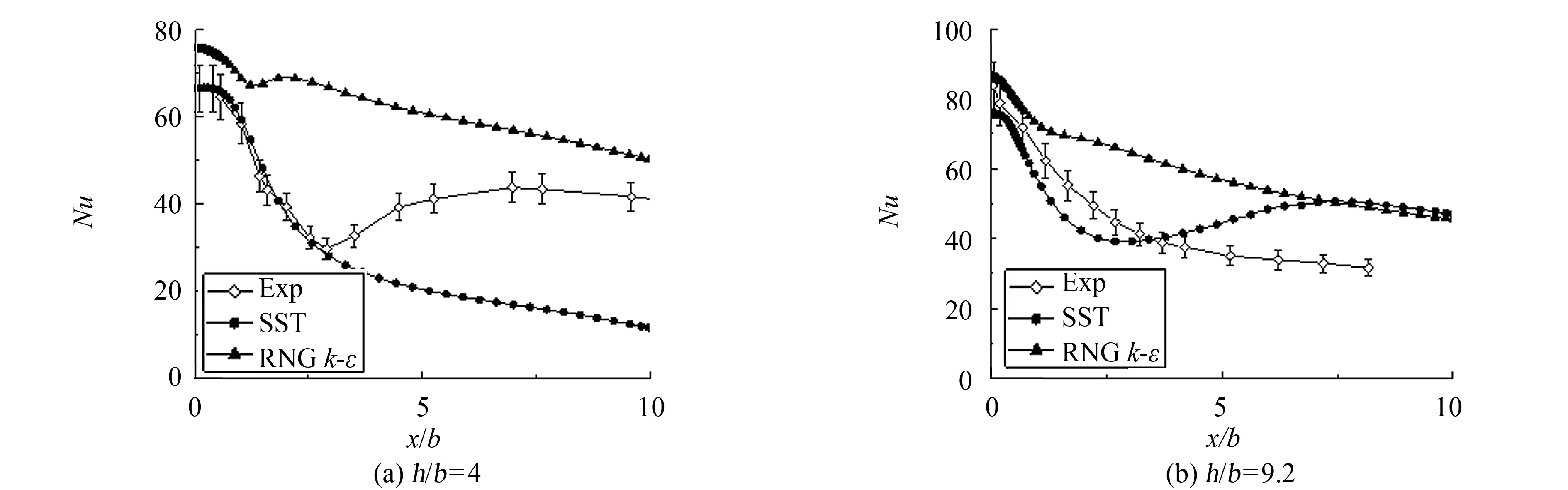
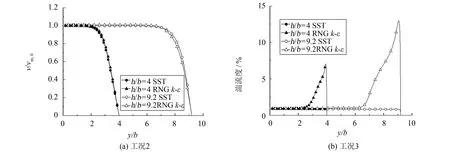
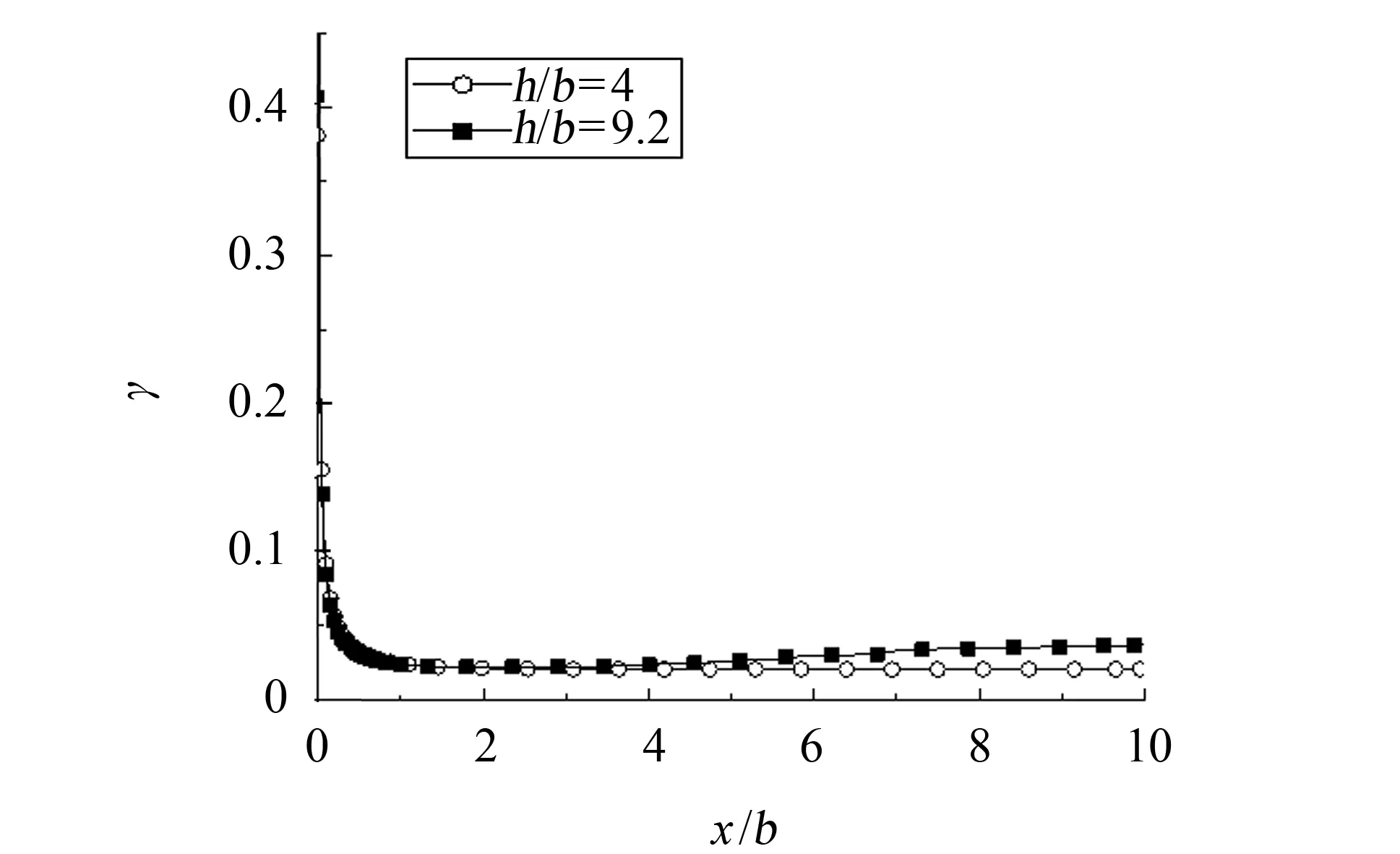
对于稳态自由射流的数值模拟,主要关注射流中心线上流动发展及射流横向发展. 图3给出了工况1射流中心线上的时均速度分布. 由图3可知,实验中射流核心区的范围大致为0 图4给出了工况7射流中心线上时均速度的分布,与前述结果类似,在核心区大小的模拟上,数值结果、理论公式均和实验存在偏差,特别地,RNGk-ε模型模拟的射流核心最小,亦即在喷嘴出口下游RNGk-ε模型模拟的湍流粘性要大于SST模型,射流与周围流体之间动量交换强烈,射流中心线上动能发生快速耗散,但就核心区下游速度衰减速率而言,两种湍流模型结果和理论公式基本一致,略快于实验结果. 图3 工况1射流中心线上时均速度分布Fig.3 Distribution of Reynolds-average velocity on jet central line of case 1 图4 工况7射流中心线上时均速度分布Fig.4 Distribution of Reynolds-average velocity on jet central line of case 7 图5 工况1射流中心线上速度脉动分布Fig.5 Distribution of velocity fluctuation on jet central line of case 1 图5给出了工况1射流中心线上速度脉动的发展. 其中数值模拟的速度脉动通过湍动能获得,如下式所示. 对照图4可知,数值模拟中,在射流核心区内速度脉动量很小,亦即湍流度很低,随着射流不断发展,湍流度逐渐增强. 而实验中虽然射流出口处速度脉动同样很小,但在射流核心区内时速度脉动已开始明显增大. 在射流末端,数值模拟的速度脉动水平和实验结果在量级上是相符的. 图6 工况7射流中心线速度脉动分布Fig.6 Distribution of velocity fluctuation on jet central line of case 7 图6给出了工况7射流中心线上速度脉动的发展,与前述结果类似,实验中核心区内已有明显速度脉动,而数值模拟仅在核心区下游才有明显速度脉动,在射流末端,数值模拟和实验的速度脉动量级相当. 射流中心线上速度脉动沿流向增大,意味着流动发展过程中湍动能增大,亦即流动的时均动能更多地通过湍流结构耗散为速度脉动,导致时均速度衰减,因此射流中心线上时均速度和脉动速度的发展是相互关联的,不同湍流模型对于湍流粘性计算结果不同,从而影响对射流中心线上流动的模拟. 图7给出了工况1射流出口及出口下游y/b=1位置上流向速度的横向分布. 由于实验条件限制,射流发展过程中速度关于中心线并不严格对称,而数值模拟并不能反应该现象,因此后续分析仅针对x/b>0的区域. 在射流出口y/b=0处,SST模型的速度分布与实验结果吻合较好,而RNGk-ε模型所得速度分布在射流边缘处与实验存在一定偏差. 图7 工况1中y/b=0和1处流向速度沿展向分布Fig.7 Distribution of streamwise velocity along spanwise at y/b=0 and 1 of case 1 图8给出了工况1中y/b=0和1处速度脉动的分布. 对于射流出口y/b=0处的速度脉动,SST模拟结果和实验吻合较好,而RNGk-ε模型在射流边缘处明显高估了速度脉动,从而造成其低估了y/b=0处射流边缘的流向速度(如图7所示). 在y/b=1处,两个湍流模型对于速度脉动的模拟总体上和实验相符. 图8 工况1中y/b=0和1处速度脉动分布Fig.8 Distribution of velocity fluctuation at y/b=0 and 1 of case 1 图9给出了工况4中y/b=0.3和1处的流向速度分布. 与前述结果类似,两个湍流模型结果的差别主要体现在射流边缘,RNGk-ε模型的结果在自由剪切层中时均速度分布较为光滑,体现出较大的湍流粘性,而SST模型在射流边缘的时均速度分布则呈现较为明显的折角. 图9 工况4中y/b=0.3和1的流向速度分布Fig.9 Distribution of streamwise velocity at y/b=0 and 1 of case 4 对于稳态冲击射流,数值和实验对比主要关注壁面射流区域的流动发展及靶面传热特性. 图10给出了工况2数值模拟得到的壁面射流区域的时均速度分布. 在滞止区附近x/b=1处,数值模拟的壁面射流流向速度整体大于实验结果; 在x/b=2处,两种湍流模型得到的壁面射流速度分布和实验整体吻合较好; 在x/b=6处,近壁区域SST模型与实验吻合较好,远离壁面区域SST模型所得速度分布整体偏大,而RNGk-ε模型与实验结果吻合较好. 图10 工况2壁面射流区域时均速度分布Fig.10 Distribution of Reynolds-average velocity in the wall jet region of case 2 图11为工况2壁面射流区域速度脉动的分布. 由图11可知,两种湍流模型结果均和实验存在明显偏差,整体而言在该区域RNGk-ε模型表现优于SST模型,SST模型计算的速度脉动均维持在较低水平,离滞止区越远与实验结果偏差越大,其主要原因是SST transition中的转捩模型考虑了壁面射流边界层的发展. 图11 工况2壁面射流区域速度脉动分布Fig.11 Distribution of velocity fluctuation in the wall jet region of case 2 图12为工况5壁面射流区域时均速度的分布,与图10情况类似,两个湍流模型对壁面射流区域时均速度的模拟大体相近,特别地,在该工况下,滞止区附近的数值模拟结果和实验吻合很好,而在远离滞止区的地方,仍然是RNGk-ε模型与实验结果更接近一些. 图12 工况5壁面射流区域时均速度分布Fig.12 Distribution of Reynolds-average velocity in the wall jet region of case 5 图13为工况2和工况3中靶面努塞尔数分布. 总体而言,数值模拟的传热结果均和实验存在较明显的偏差. 在滞止区附近(x/b<3),SST模型结果和实验比较吻合,RNGk-ε模型结果明显偏大,且在工况2的模拟中出现了实验中不存在的二次峰值; 在远离滞止区的地方(x/b>3),工况2的实验结果呈现沿壁面射流流向Nu增大的趋势,而数值模拟结果均呈现沿流向单调递减的趋势,工况3中实验靶面Nu沿流向单调递减,而SST模拟结果在远离滞止区的地方出现了二次峰值,与实验不符. 总体而言,对于靶面传热的模拟,SST模型在滞止区附近表现较好,而RNGk-ε模型总体高估了壁面努塞尔数. 图13 工况2和工况3靶面Nu分布Fig.13 Distribution of Nusselt number in the wall of case 2 and 3 图14给出了工况2和3射流中心线上速度和湍流度的数值模拟结果. 图14 工况2和工况3中射流中心线上时均速度和湍流度的分布Fig.14 Distribution of Reynolds-average velocity and turbulent intensity on jet central line of case 2 and 3 由图14可知,在该工况下,RNGk-ε和SST湍流模型在模拟冲击射流中心线速度衰减上没有明显差别,分析其原因,可能是由于当射流雷诺数较大时,与惯性力相比,湍流粘性对于流动的影响小得多,因而不同湍流模型计算结果的差别也较小. 而在冲击射流临近靶面区域,RNGk-ε和SST湍流模型关于湍流度的计算结果存在明显不同:RNGk-ε模型在滞止区附近湍动能显著增大. 该现象在公开文献中已有共识[13-17],k-ε模型及其变种在模拟冲击滞止区域的流动时会高估当地的湍动能,虽然一些修正有助于抑制该现象,但作用有限,滞止区域湍动能过大将进一步造成滞止区域传热过预测,此即图13中滞止区域传热RNGk-ε模型结果高于SST的原因. 图15 SST湍流模型结果中工况2和工况3靶面间歇因子γ分布Fig.15 Distribution of intermittency γon the target wall in case 2 and 3 by SST turbulence model 图15给出了工况2和3的SST湍流模型结果中靶面近壁处间歇因子γ的分布,由图15可知,SST模拟的工况2中壁面未出现层流向湍流的转捩,而工况3中在壁面x/b≈3处发生转捩,因此图13中的SST对工况2靶面的传热模拟未见二次峰值,而对工况3靶面的传热模拟结果则呈现二次峰值,图13中SST模型对于靶面传热二次峰值模拟与实验存在偏差,说明其对靶面边界层转捩的模拟与实验存在偏差. 对于任一工况,虽然RNGk-ε湍流模型相比于SST模型会高估滞止区域湍流度,但这并不意味着对于该工况RNGk-ε模型模拟结果中滞止区传热一定高于SST模型结果,因为滞止区域传热是射流冲击速度和当地湍流度共同作用的结果,而在一些工况下RNGk-ε模型结果中射流速度衰减过快,反而会造成其冲击滞止区域换热弱于SST模型,如图16所示为工况8数值结果,虽然RNGk-ε模型结果在滞止区仍表现出很大的湍动能,但由于射流中心线上时均速度衰减太快,使得其靶面传热结果要小于SST模型的结果. 图16 工况8传热特性及射流中心线上流动特征Fig.16 Heat transfer characteristics and the jet flow characteristics of center line of case 8 通过对公开文献中二维槽缝冲击射流问题的数值模拟,考察了RNGk-ε湍流模型和Transition SST湍流模型对稳态冲击射流问题的适用性,研究结果表明: 1) RNGk-ε模型模拟的射流中心线上湍流度要强于Transition SST模型,且RNGk-ε模型的射流出口速度横向分布中速度边界层比实验结果更厚,表现出更强的湍流粘性作用. 2) 对于射流雷诺数较小的工况,RNGk-ε模型在射流中心线上表现出较强的湍流粘性,从而使得射流中心线上雷诺时均速度衰减较快; 对于射流雷诺数较大的工况,流体惯性力较大,湍流粘性的影响较小,两个湍流模型模拟的射流中心线上雷诺时均速度分布相差不大. 3) 对于射流雷诺数较大的工况,受湍动能的影响,RNGk-ε模型结果中滞止区的传热要高于SST模型; 对于射流雷诺数较小的工况,受射流中心线上雷诺时均速度衰减的影响,RNGk-ε模型结果中滞止区传热要低于SST模型结果. 4) 对于壁面射流区域的模拟,RNGk-ε模型在雷诺时均速度和速度脉动的计算上要略优于SST模型,但传热模拟并没有表现出更好的适用性. 综上,对于稳态冲击射流问题的模拟,就研究所涉及工况,Transition SST湍流模型要略优于RNGk-ε模型,特别是在模拟射流出口速度分布、射流中心线速度及湍流度发展、滞止区域的传热等方面. [1] ZUCKERMAN N, LIOR N. Jet impingement heat transfer: physics, correlations, and numerical modeling[J]. Advances in Heat Transfer, 2006, 39(6): 565-631. [2] MONTAZERI H, HANNANI S K, FARHANIEH B. Turbulent flow using a modified V2f turbulence model[C]//ASME 2004 International Mechanical Engineering Congress and Exposition. Anaheim:American Society of Mechanical Engineers, 2004: 587-594. [3] LI W, REN J, JIANG H,etal. Assessment of six turbulence models for modeling and predicting narrow passage flows, part 1: impingement jets[J]. Numerical Heat Transfer, Part A: Applications, 2016, 69(5): 445-463. [4] HOFMANN H M, KAISER R, KIND M,etal. Calculations of steady and pulsating impinging jets-an assessment of 13 widely used turbulence models[J]. Numerical Heat Transfer, Part B: Fundamentals, 2007, 51(6): 565-583. [5] ISMAN M K, PULAT E, ETEMOGLU A B,etal. Numerical investigation of turbulent impinging jet cooling of a constant heat flux surface[J]. Numerical Heat Transfer, Part A: Applications, 2008, 53(10): 1 109-1 132. [6] SHARIF M A R, MOTHE K K. Evaluation of turbulence models in the prediction of heat transfer due to slot jet impingement on plane and concave surfaces[J]. Numerical Heat Transfer Part B: Fundamentals, 2009, 55(4): 273-294. [7] ASHFORTH-FROST S, JAMBUNATHAN K, WHITNEY C F. Velocity and turbulence characteristics of a semiconfined orthogonally impinging slot jet[J]. Experimental Thermal and Fluid Science, 1997, 14(1): 60-67. [8] ZHE J, MODI V. Near wall measurements for a turbulent impinging slot jet (data bank contribution)[J]. Journal of Fluids Engineering, 2001, 123(1): 112-120. [9] MLADIN E C, ZUMBRUNNEN D A. Local convective heat transfer to submerged pulsating jets[J]. International Journal of Heat and Mass Transfer, 1997, 40(14): 3 305-3 321. [10] YAKHOT V, ORSZAG S A, THANGAM S,etal. Development of turbulence models for shear flows by a double expansion technique[J]. Physics of Fluids A: Fluid Dynamics, 1992, 4(7): 1 510-1 520. [11] MENTER F R, LANGTRY R B, LIKKI S R,etal. A correlation-based transition model using local variables: part I- model formulation[J]. Journal of Turbo Machinery, 2004, 128(3): 413-422. [12] AZIZ T N, RAIFORD J P, KHAN A A. Numerical simulation of turbulent jets[J]. Engineering Applications of Computational Fluid Mechanics, 2008, 2(2): 234-243. [13] ACHARI A M, DAS M K. Application of various RANS based models towards predicting turbulent slot jet impingement[J]. International Journal of Thermal Sciences, 2015, 98: 332-351. [14] BOVO M, DAVIDSON L. On the numerical modeling of impinging jets heat transfer-a practical approach[J]. Numerical Heat Transfer, Part A: Applications, 2013, 64(4): 290-316. [15] ALIMOHAMMADI S, PERSOONS T, MURRAY D B. A numerical-experimental study of heat transfer enhancement using unconfined steady and pulsating turbulent air jet impingement[C]//15th International Heat Transfer Conference (IHTC-15). Kyoto: [s.n.],2014: 10-15. [16] DUTTA R, DEWAN A, SRINIVASAN B. Comparison of various integration to wall (ITW) RANS models for predicting turbulent slot jet impingement heat transfer[J]. International Journal of Heat and Mass Transfer, 2013, 65(5): 750-764. [17] PRAMANIK S, ACHARI A M, DAS M K. Numerical simulation of a turbulent confined slot impinging jet[J]. Industrial & Engineering Chemistry Research, 2012, 51(26): 9 153-9 163.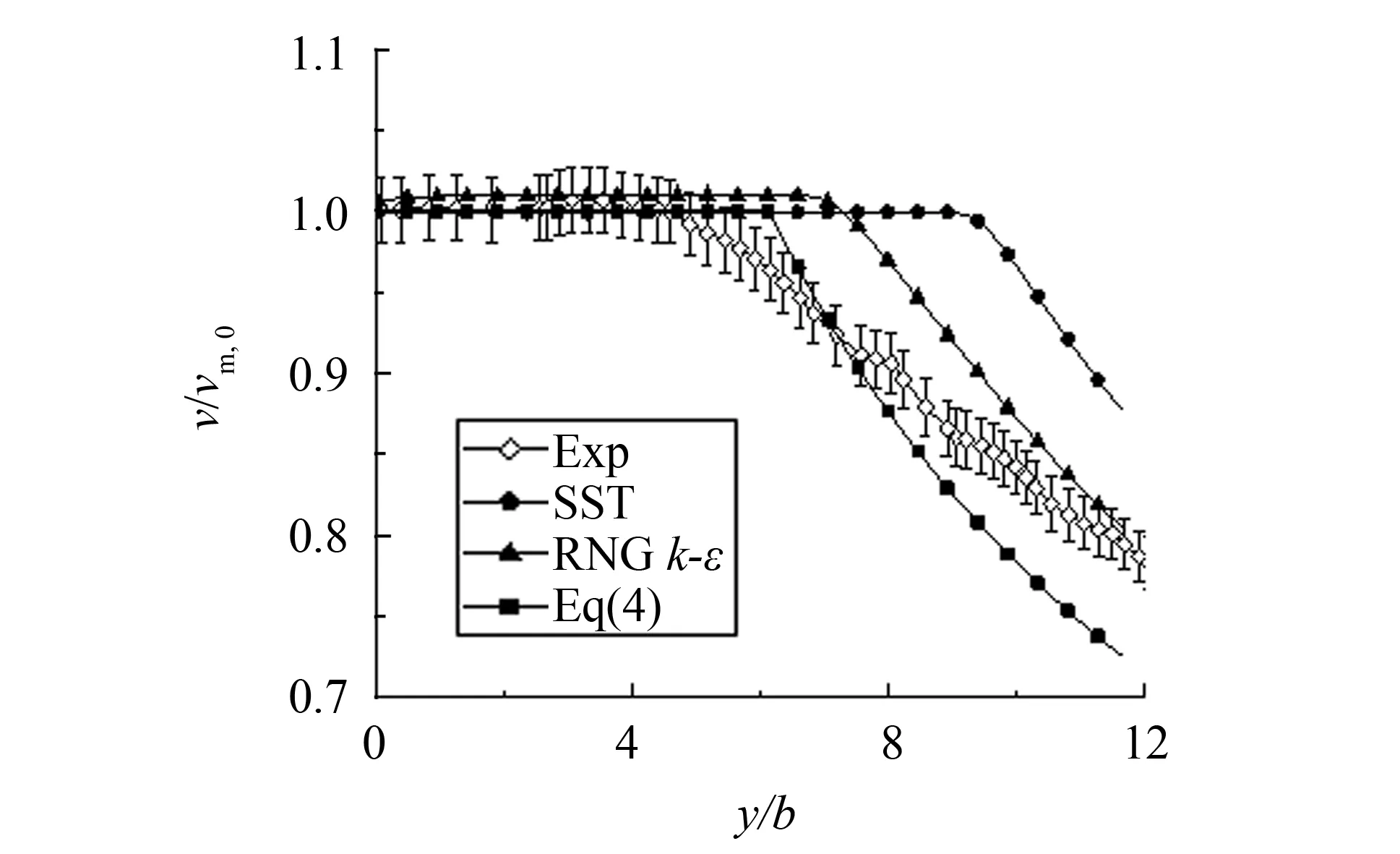

3.2 稳态冲击射流



4 结语

