中能重离子反应中中子-质子有效质量劈裂的研究

,,

(上海理工大学 理学院,上海 200093)

在实验上研究重离子反应,需要用到重离子加速器,实验的成本很高,所以,通常用计算机模拟核反应.人们用QMD (量子分子动力学)模型对重离子反应进行了大量的研究.Zhang等[17]利用改进的QMD模型研究了重离子反应中的同位素分布、中质比、氚/氦3比等同位旋效应,采用多种Skyrme参数研究了同位旋扩散、对称能、核子有效质量分裂与动量相关作用[18].李庆丰等[19]考虑了Skyrme势能密度函数,用极端相对论量子分子动力学(UrQMD)模型研究了197Au+197Au重离子碰撞中的自旋轨道耦合效应.Xie等[20]也对197Au+197Au的碰撞进行了研究,发现对于中子-质子有效质量劈裂,中子-质子差分集体流是一个有效的探针.郭文军等用同位旋相关的QMD模型研究了12C与Al同位素的反应截面[21],激发态56Ni反应的原子核阻止[22],重离子反应中由中子-质子轫致辐射产生的光子以及它与对称势的关系[23],光核反应中的核子发射数及其与截面的关系[24].

本文与前人工作的最大的区别是利用同位旋相关的QMD模型对中能重离子反应进行模拟,通过修改动量相关势,得出不同的中子-质子有效质量劈裂的值,根据这些不同的值来研究其对原子核阻止、核子发射数的影响,并与实验上测定的原子核阻止和核子发射数进行比较.这样的研究不仅可以确定有效质量劈裂值,而且可以给出其与原子核阻止、核子发射数的关联性.

1 模 型

利用量子分子动力学[25-28]模型来模拟重离子反应.为了考虑同位旋效应对重离子反应过程的影响,对传统的量子分子动力学模型作了适当的修改.密度相关的平均场的计算需要考虑质子和中子的区别(库仑势和对称势),计算核子-核子反应截面和泡利阻塞时也要区分质子和中子.通过这些修改,得到了改进的同位旋相关的量子分子动力学(IQMD)[29]模型,它的平均场势能U的表达式为

U=USky+UYuk+UCoul+UMDI+UPauli+Usym

(1)

动量相关作用UMDI可表示为[31]

(2)

式中:ρ0=0.16 fm-3表示原子核饱和密度;ρ表示原子核密度;t4,t5为参数;p1-p2表示两粒子的动量差.

中子-质子有效质量劈裂描述的是中子、质子的势能在动量方向上的梯度差.原有的QMD模型动量相关的部分没有考虑中子和质子的差别,所以,无法研究有效质量劈裂对反应的影响.本文在动量相关作用中引入了中子、质子的差别,将式(2)修改为同位旋相关的动量相关作用.

(3)

(4)

式中:Un,Up分别为同位旋相关的中子、质子的动量相关作用势;t4,t5n,t5p为参数.

中子、质子的费米动量[14]

(5)

(6)

当有效质量劈裂的平均值取0.31δ,0.41δ,0.51δ时,根据要求计算不同密度、不同相对中子过剩下的有效质量劈裂值,继而确定t4,t5n,t5p的值.通过调整t4,t5n,t5p的值,增加动量相关的势能部分,再调整对称势的强度系数c的值,使对称势部分相应地减少相同的量,使整个核在饱和点密度附近的对称能恢复到原始状态,这样,整个核势仍旧满足各种实验所约束的条件.不同参数和有效质量劈裂的值如表1所示.

表1 不同参数和有效质量劈裂的值Tab.1 Different parameters and the values of the effective mass splitting

在图1中,由上部分的图可以看出,两核子动量差Δp很大时,6条线几乎重叠在一起,这是因为核子体系能量较大,起主导作用,有效质量劈裂所带来的能量差异相对于系统的能量差异可以忽略不计.两核子的动量差不大时(12～22 MeV),动量相关作用对其影响最明显.其中,有效质量劈裂为0.31δ时的动量相关作用最大,有效质量劈裂为0.51δ时的动量相关作用最小.进一步研究了有效质量劈裂带来的动量相关作用的同位旋效应,图1的下部分表明,两核子动量差很小时(12 MeV以下),动量相关作用所引起的对称能的变化很小,有效质量劈裂对动量相关作用的同位旋效应影响很小.两核子动量差较大时,动量相关作用所引起的对称能的变化很大,有效质量劈裂对动量相关作用的同位旋效应影响越来越强.也就是说,有效质量劈裂通过对称能的不同来影响核反应的状态.有效质量劈裂越大,中子和质子的动量相关作用差别越大,即对称能越大,动量相关作用的同位旋效应越明显.所以,有效质量劈裂与系统的对称能紧密相关,是描述动量相关作用的物理量.

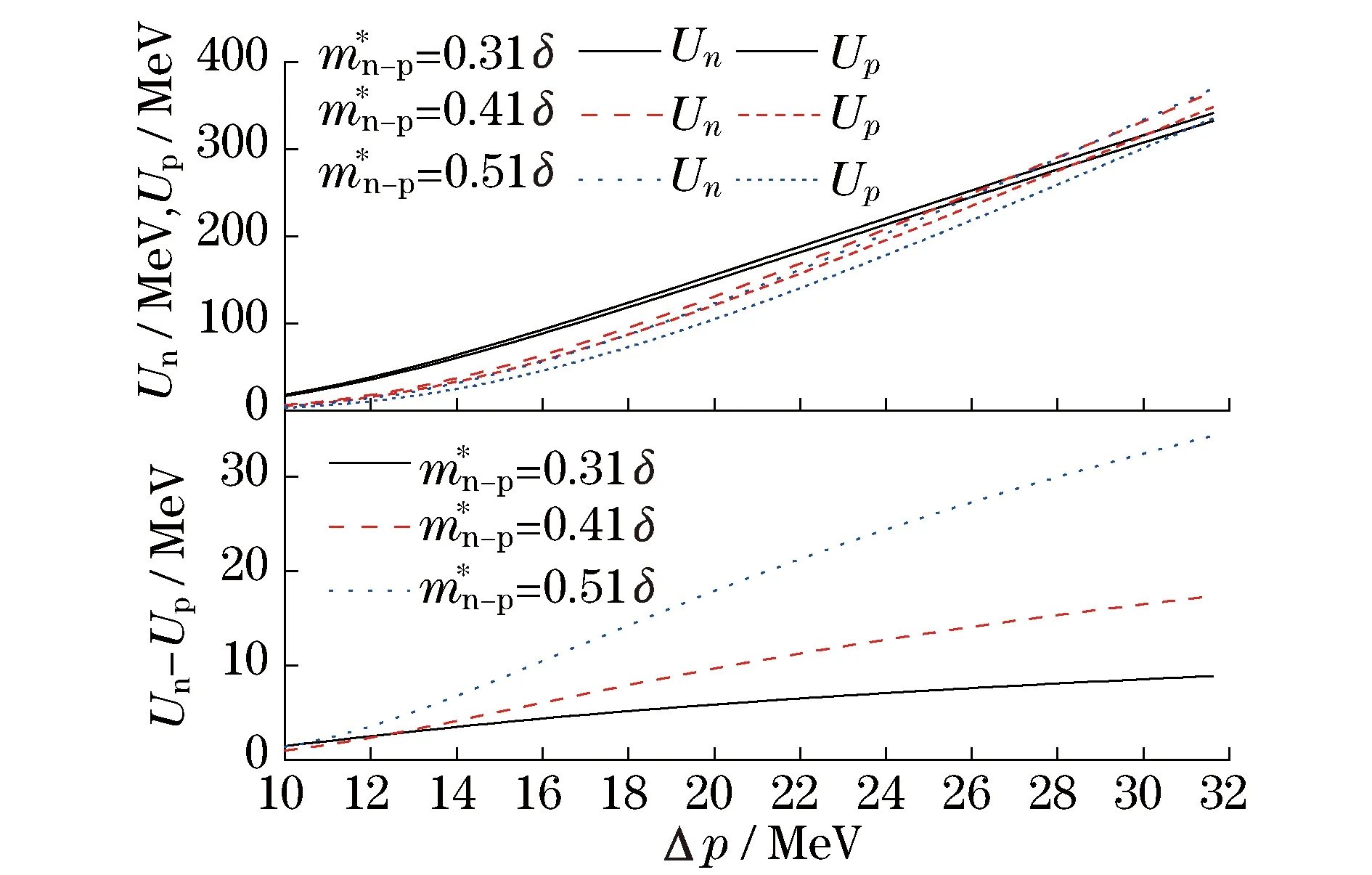
图1 不同有效质量劈裂的中子、质子势能及其差值随相对动量的变化Fig.1 Relationship between the neutron and proton potential energy and their difference variation with different effective mass splitting and relative momentum

图2是参数t4,t5n,t5p选取适当值时,用表1所示的3套参数计算得到的有效质量劈裂在0.31δ,0.41δ,0.51δ周围随密度和相对中子过剩的演化.由图2可以看出,当δ相同时,随着密度的增加,有效质量劈裂的值先增加后减小.在δ=0.15时作一条横线,可以看出,密度较高时,有效质量劈裂在0.31δ周围时,其变化最缓慢,在0.51δ周围时,其变化最剧烈.而在核反应的压缩过程中,密度可以达到饱和密度的2～3倍,所以,不同的有效质量劈裂对压缩过程影响很大.密度较低时,有效质量劈裂在0.51δ周围时变化剧烈,会迅速降低为零,同位旋相关的动量相关作用对核反应影响变弱.而核反应过程中的膨胀和碎裂过程正处于该密度范围,所以,不同的有效质量劈裂对碎片的形成影响很大.

图2 有效值劈裂随密度和相对中子过剩的演化Fig.2 Evolution of the effective mass splitting with the density and relative neutron excesses

2 结果与讨论

原子核阻止R[2,32-33]是在重离子碰撞过程中决定反应结果(终态产物)的一个重要物理量,可以用来描述同位旋自由度逐渐从非平衡向平衡过渡的过程[34],其具体形式为

(7)

从式(7)可以看出,原子核阻止反映了核子间碰撞的激烈程度.前面的研究表明,动量相关作用较大时,原子核阻止较大[35].而有效质量劈裂取不同值时,其动量相关作用不同,所以,有效质量劈裂会对原子核阻止产生影响.本文比较了不同的中子-质子有效质量劈裂对原子核阻止的影响.

图3(见下页)表示112Sn+112Sn,124Sn+124Sn和132Sn+132Sn分别在能量E=50,100,200 MeV/u反应系统中原子核阻止随反应时间t的演化过程.图中3条线分别表示中子-质子有效质量劈裂为0.31δ,0.41δ,0.51δ时的原子核阻止.由图3可以清楚地看出,中子-质子有效质量劈裂的大小对原子核阻止有明显的影响,无论何种反应系统,在低能且动量差Δp=12～22 MeV时,中子-质子有效质量劈裂在0.31δ时,原子核阻止R总是最大的.这是因为,由图1可知,中子-质子有效质量劈裂在0.31δ时动量相关作用比较大,总的体系能量较大,截面降低,所以,原子核阻止变大.中子-质子有效质量劈裂为0.41δ和0.51δ时,原子核阻止几乎相同.根据图1的上部分可以得到中子-质子有效质量劈裂为0.51δ时,动量相关作用的绝对大小小,所以,原子核阻止较小.而从图1的下部分可以得到,当中子-质子有效质量劈裂为0.51δ时,动量相关作用的中子-质子的相对大小大,中子、质子动量相关作用差越大,同位旋效应越明显,原子核阻止越大.影响原子核阻止的两个因素相互竞争,所以,中子-质子有效质量劈裂为0.41δ和0.51δ时,两条曲线几乎重叠在一起.中子-质子有效质量劈裂为0.31δ的绝对大小大于中子-质子有效质量劈裂为0.41δ和0.51δ的绝对大小,所以,动量相关作用的绝对大小的影响占主导地位,而中子、质子动量相关作用的差的影响占从属地位.能量为200 MeV时,即能量较高时,体系的能量远大于动量相关作用的能量时,中子-质子有效质量劈裂对其原子核阻止影响很小,所以,在能量较高时,有效质量劈裂对原子核阻止影响很小.

图4表示112Sn+112Sn,124Sn+124Sn和132Sn+132Sn分别在能量为50,100,200 MeV/u反应系统中中子、质子发射数随有效质量劈裂的变化.

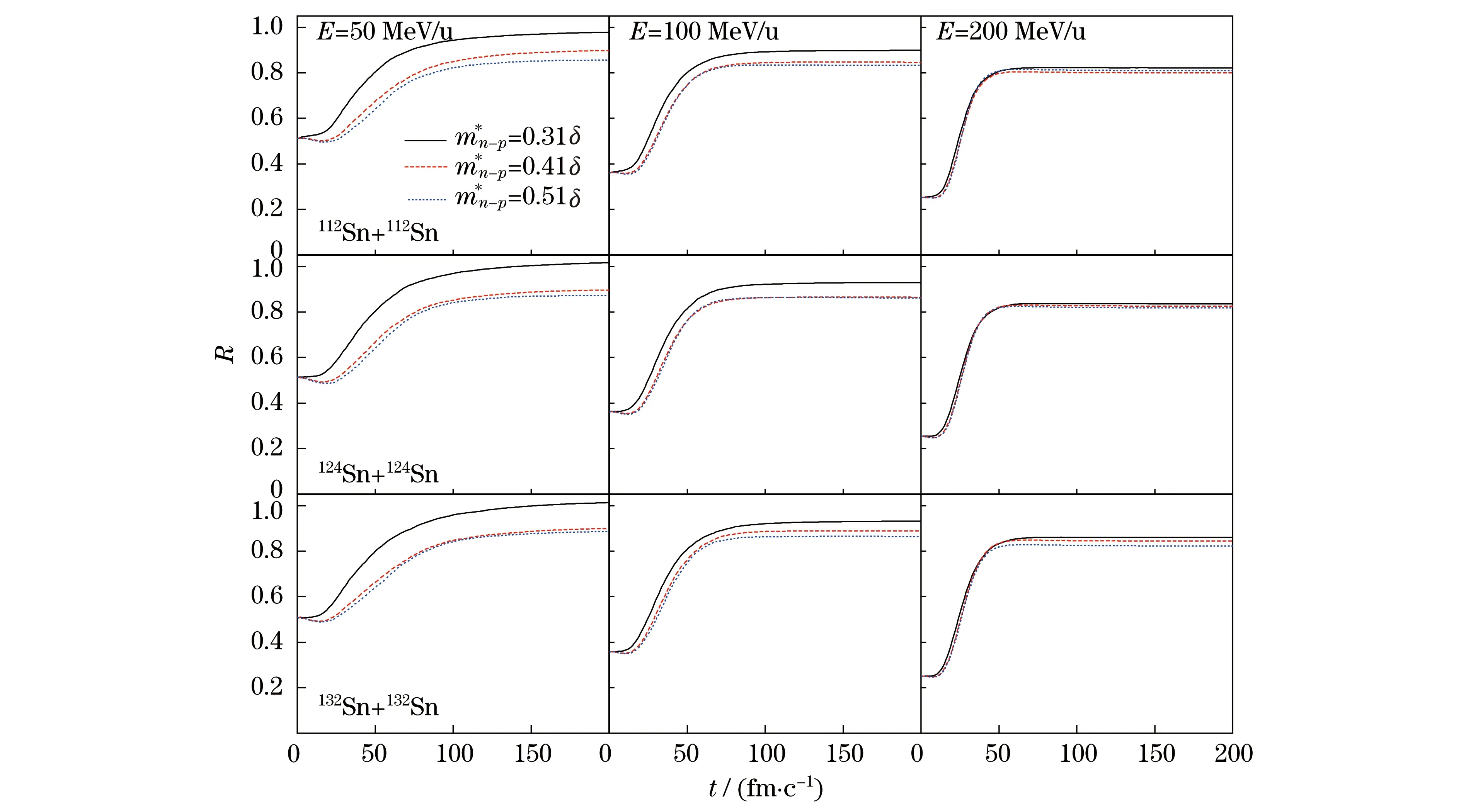
图3 不同有效质量劈裂的原子核阻止R随时间t演化过程Fig.3 Evolution of the nuclear stopping over time with different

图4 中子、质子发射数随有效质量劈裂的变化Fig.4 Evolution of the neutron numbers and proton numbers with the effective mass splitting

在图4中可以明显看出,反应能量越高,中子和质子发射数越多.在相同的能量下,有效质量劈裂分别在0.31δ,0.41δ,0.51δ时,中子和质子发射数是依次递减的.也就是说,中子、质子发射数是随着有效质量劈裂的增加而减少的.同样,由图1的上部分可以看出,有效质量劈裂越大,动量相关作用越小,总的能量越低,所以,中子、质子发射数就少.从图4的任意一张图中可以看到,两条曲线中间的间隔相差不大,也就是说,中子发射数与质子发射数的差几乎保持不变,不同的有效质量劈裂对其发射的相对大小影响较小.有效质量劈裂对中子、质子发射数的影响同时增加,同时减少.反应系统能量越高时,中子、质子发射数的两条线的间隔越来越宽,所得结论和文献[36]相同.

3 结 论

通过修改QMD模型中的初始化程序,分析了中子-质子有效质量劈裂对中能重离子反应的影响.利用同位旋相关的QMD模型对中能重离子反应进行了模拟,在前人经验的基础上,通过修改动量相关势得出不同的有效质量劈裂,从而完善中能重离子碰撞的输运理论.通过对上述问题的模拟计算研究,可以得出以下的结论:

a.中子-质子有效质量劈裂对原子核阻止R有很明显的影响.动量相关作用的相对大小和绝对大小相互竞争,共同作用到原子核阻止上.中子-质子有效质量劈裂值不同时,在高能时原子核阻止几乎重合,在低能时差别较大,因此,建议选取低能情况来研究有效质量劈裂对核反应的影响.

b.中子-质子有效质量劈裂对中子、质子发射数有很明显影响.随着中子-质子有效质量劈裂的增加,会使中子、质子发射数减少.

c.可以通过实验上测得的原子核阻止和中子、质子发射数,得到与中子-质子的有效质量劈裂相关的信息.

[1] FENG Z Q,XIE W J,CHEN P H,et al.In-medium and isospin effects on particle production near threshold energies in heavy-ion collisions[J].Physical Review C,2015,92(4):044604.

[2] TIAN J,YE W.Isospin effect on probing nuclear dissipation with fission cross sections[J].Physical Review C,2016,94(2):021601.

[3] 刘建业,陈波,赵强,等.中能重离子碰撞中同位旋效应的灵敏探针[J].原子核物理评论,1999,16(3):165-168.

[4] 张丰收.同位旋相关的输运理论[J].原子核物理评论,1999,16(3):169-176.

[5] YENNELLO S J,YOUNG B,YEE J,et al.The use of radioactive nuclear beams to study the equilibration of the NZ degree of freedom in intermediate-energy heavy-ion reactions[J].Physics Letters B,1994,321(1/2):15-19.

[6] WADA R,HILDENBRAND K D,LYNEN U,et al.Isotopic-yield ratios of complex fragments from intermediate-energy heavy-ion reactions[J].Physical Review Letters,1987,58(18):1829-1832.

[7] KUNDE G J,GAFF S J,GELBKE C K,et al.Multifragment Production in Reactions of112Sn+112Sn and124Sn+124Sn atE/A=40 MeV[J].Physical Review Letters,1996,77(14):2897-2900.

[8] RAMI F,LEIFELS Y,DE SCHAUENBURG B,et al.Isospin tracing:a probe of nonequilibrium in central heavy-ion collisions[J].Physical Review Letters,2000,84(6):1120-1123.

[9] PAK R,BENENSON W,BJARKI O,et al.Isospin dependence of collective transverse flow in nuclear collisions[J].Physical Review Letters,1997,78(6):1022-1025.

[10] LI B A,KO C M,REN Z Z.Equation of state of asymmetric nuclear matter and collisions of neutron-rich nuclei[J].Physical Review Letters,1997,78(9):1644-1647.

[11] LI B A,REN Z Z,KO C M,et al.Isospin dependence of collective flow in heavy-ion collisions at intermediate energies[J].Physical Review Letters,1996,76(24):4492-4495.

[12] LI B A.Constraining the neutron-proton effective mass splitting in neutron-rich matter[J].Physical Review C,2004,69(6):064602.

[13] XU C,LI B A,CHEN L W.Symmetry energy,its density slope,and neutron-proton effective mass splitting at normal density extracted from global nucleon optical potentials[J].Physical Review C,2010,82(5):054607.

[14] LI B A,HAN X.Constraining the neutron-proton effective mass splitting using empirical constraints on the density dependence of nuclear symmetry energy around normal density[J].Physics Letters B,2013,727(1/3):276-281.

[15] LI X H,GUO W J,LI B A,et al.Neutron-proton effective mass splitting in neutron-rich matter at normal density from analyzing nucleon-nucleus scattering data within an isospin dependent optical model[J].Physics Letters B,2015,743:408-414.

[16] LI B A,CHEN L W.Neutron-proton effective mass splitting in neutron-rich matter and its impacts on nuclear reactions[J].Modern Physics Letters A,2015,30(13):1530010.

[17] ZHANG Y X,LI Z X,ZHOU C S,et al.Effect of isospin-dependent cluster recognition on the observables in heavy ion collisions[J].Physical Review C,2012,85(5):051602.

[18] ZHANG Y X,TSANG M B,LI Z X,et al.Constraints on nucleon effective mass splitting with heavy ion collisions[J].Physics Letters B,2014,732:186-190.

[19] GUO C C,WANG Y J,LI Q F,et al.Effect of the spin-orbit interaction on flows in heavy-ion collisions at intermediate energies[J].Physical Review C,2014,90(3):034606.

[20] XIE W J,ZHANG F S.Nuclear collective flows as a probe to the neutron-proton effective mass splitting[J].Physics Letters B,2014,735:250-255.

[21] YANG L M,GUO W J,ZHANG F,et al.Study of the total reaction cross section via QMD[J].Chinese Physics C,2013,37(10):104101.

[22] ZHANG A,GUO W J,HUANG J W,et al.Isospin effect of the in-medium nucleon-nucleon cross section in excited nuclear reactions[J].Chinese Physics C,2014,38(5):054103.

[23] YANG L M,GUO W J,ZHANG Y P,et al.Probing the symmetry potential with neutron-proton bremsstrahlung in heavy-ion collisions[J].Chinese Physics C,2014,38(7):074105.

[24] GUO W J,HUANG J W,YONG G C,et al.Nucleon emission number as a probe of isospin-dependent N-N cross section in photonuclear reactions[J].Chinese Physics Letters,2014,31(10):102501.

[25] DI TORO M,BARAN V,COLONNA M,et al.Isospin dynamics at medium energies[J].Progress in Particle and Nuclear Physics,1999,42:125-136.

[26] AICHELIN J,STOCKER H.Quantum molecular dynamics——A novel approach to N-body correlations in heavy ion collisions[J].Physics Letters B,1986,176(1/2):14-19.

[27] CHEN L W,ZHANG F S,JING G M.Analysis of isospin dependence of nuclear collective flow in an isospin-dependent quantum molecular dynamics model[J].Physical Review C,1998,58(4):2283-2291.

[28] PEILERT G,STÖCKER H,GREINER W,et al.Multifragmentation,fragment flow,and the nuclear equation of state[J].Physical Review C,1989,39(4):1402-1419.

[29] AICHELIN J,PEILERT G,BOHNET A,et al.Quantum molecular dynamics approach to heavy ion collisions:description of the model,comparison with fragmentation data,and the mechanism of fragment formation[J].Physical Review C,1988,37(6):2451-2468.

[30] LANGANKE K,MARUHN J,KOONIN S E.Computational nuclear physics 1:nuclear structure[M].Berlin Heidelberg:Springer-Verlag,1991.

[31] XU J,MARTINOT Z,LI B A.Disentangling effects of collision geometry and symmetry energy in U+U collisions[J].Physical Review C,2012,86(4):044623.

[32] LIU J Y,GUO W J,WANG S J,et al.Nuclear stopping as a probe for in-medium nucleon-nucleon cross sections in intermediate energy heavy ion collisions[J].Physical Review Letters,2001,86(6):975-978.

[33] BUSZA W,LEDOUX R.Energy deposition in high-energy proton-nucleus collisions[J].Annual Review of Nuclear and Particle Science,1988,38(1):119-159.

[34] LI B A,YENNELLO S J.Isospin nonequilibrium in heavy-ion collisions at intermediate energies[J].Physical Review C,1995,52(4):R1746.

[35] LIU J Y,GUO W J,XING Y Z,et al.Influence of a momentum dependent interaction on the isospin dependence of fragmentation and dissipation in intermediate energy heavy ion collisions[J].Physical Review C,2003,67(2):024608.

[36] LIU J Y,GUO W J,XING Y Z,et al.Probing the isospin dependent in-medium nucleon-nucleon cross section by nucleon emissions[J].Physics Letters B,2002,540(3/4):213-219.