不同引水条件对某长距离输水隧洞泥沙冲淤的影响
尹宏伟
(山西省水利水电科学研究院 山西太原 030002)
0 引言
泥沙问题的处理是引水工程的主要问题之一,其中围绕泥沙长距离输送技术的研究更为生产之急需。无压隧洞泥沙淤积问题是引水工程中必须解决的问题,当引水隧洞发生淤积时,就会影响到整个引水工程的安全运行。
某输水隧洞由黄河引水,全长15.53 km,设计流量为23.57 m3/s,纵坡1/3 000。洞断面分别采用城门洞形和马蹄形。隧洞上接泵站出水池,下游出口接桥头倒虹。受水库运用、上游来流等诸多因素影响,取水口引水引沙过程非常复杂。挟沙水流进入隧洞后,泥沙在隧洞内难免发生冲淤不平衡的情况,特别是局部地段累积性淤积的情况也可能发生。一旦隧洞内发生泥沙淤堵,将会严重影响到工程的正常运用。开展取水输水泥沙问题的深入研究,对保障隧洞输水工程的正常运行是不可或缺的。
本文通过数学模型计算,研究不同方案下含沙水流在隧道洞内的泥沙冲淤情况。具体包括:在不同引水引沙过程下,隧道洞内的泥沙冲淤变化过程;隧道洞内泥沙冲淤达到相对冲淤平衡时的纵剖面形态以及冲淤平衡年限。
1 数学模型的建立
1.1 控制方程式
本模型属于准二维恒定流非均匀悬移质非饱和输沙模型,可用来模拟水深、流速、水面比降、悬移质含沙量及其级配、床沙级配等水力泥沙要素随时间和沿流程的变化。模型所依据的基本控制方程有水流连续方程、水流运动方程、泥沙连续方程、悬移质扩散方程、水流阻力计算公式和水流挟沙力计算公式,其形式为:
水流连续方程式:

水流运动方程式:

泥沙连续方程式(分粒径组):
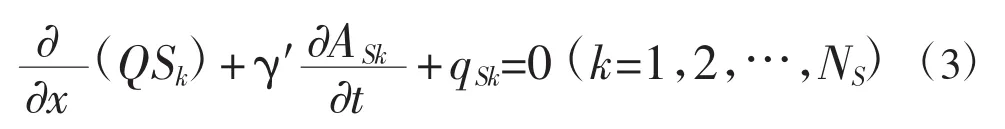
悬移质扩散方程(分粒径组):
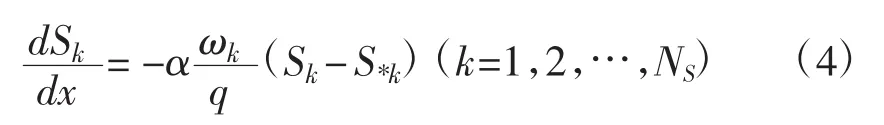
式中,Q为断面平均流量(m3/s),qL为侧向入流量(m3/s),Z为水位(m),αe为动能修正系数,ξ为局部水头损失系数,V为断面平均流速(m/s),K=ACR1/2为流量模数[其中A为过水断面面积(m2),R为水力半径(m)为谢才系数,n为糙率],S、S*分别为断面平均含沙量和水流挟沙力(kg/m3),γ′为泥沙干容重(N/m3),As为泥沙冲淤面积(m2),qsk为单位流程上第k粒径组泥沙的侧向输沙率(kg/s)(入为正,出为负),k为粒径组角标,Ns是粒径分级总数,α是恢复饱和系数,ω 是平均沉速(cm/s),q 是单宽流量(m2/s),g 是重力加速度(m/s2),x、t分别是流程和时间(s)。
1.2 水流挟沙力计算
本模型不区分床沙质和冲泻质,我们采用如下形式的公式计算的水流挟沙力:
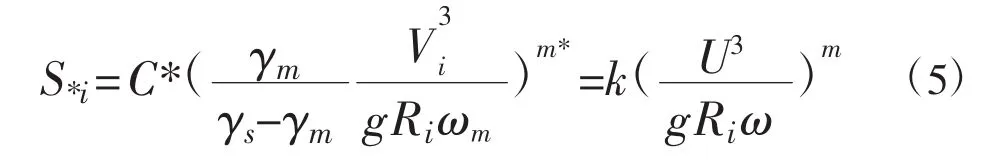
式中,S*i为i断面上混合沙(包括床沙质和冲泻质)的总挟沙力,C*、k、m*、m为待定系数和指数,根据实测资料确定;γm、γs分别为浑水和泥沙的容重;Vi、Ri分别为断面的平均流速和水力半径;ωm为混合沙挟沙力的代表沉速。混合沙挟沙力的代表沉速ωm与挟沙力的级配有关,挟沙力级配一旦确定,断面的分组挟沙力也就确定了。
1.3 床沙级配的调整及计算方法
本模型采用分层储存床沙级配模式。任一计算时段内假定泥沙的冲淤只与表层床沙发生关系。依据该时段内各粒径组泥沙的冲淤量以及表层床沙的级配,即可计算出时段末表层床沙的级配。
2 模型的验证
为了使前述泥沙数学模型能正确应用,要利用物理模型试验结果对数学模型进行率定及验证,由此确定数学模型中挟沙力系数、恢复饱和系数等参数,并应用于输水隧洞全段的冲淤数值模拟。经与物理模型试验结果验证,确定挟沙力系数k值为0.025,m值为0.75,冲刷恢复饱和系数1.0,淤积恢复饱和系数0.5。
3 输水隧洞泥沙冲淤计算结果
3.1 方案一
3.1.1 模型计算范围及地形资料
依据隧洞地形图,将15.522 km的隧洞划分为313段,控制断面共314个,沿隧洞走向,按照距上游泵站出水池的距离进行桩号编排。
3.1.2 计算时间步长划分
本系列计算时间总长为5年。时间步长划分为每天一个计算时段,5年水沙系列共计1 827个计算时段,主要用于确定冲淤平衡年限。
3.1.3 水沙资料
水沙资料根据本次计算技术要求提供的8个流量界值和3个含沙量界值结合24个水沙组合作为模拟水沙条件(见表1),这24个水沙组合流量由小到大、含沙量由小到大即作为前24天的水沙资料,之后依次重复排列构成共5年的水沙资料。

表1 水沙条件
3.1.4 下游边界条件
隧洞出口接桥头倒虹相对高程为18.280 m,可将隧洞过流状态看成明渠均匀流,进行试算得出其泄流曲线,计算成果见图1。
3.1.5 隧洞纵剖面变化及对比
按照系列水沙条件计算,隧洞运行5年隧洞进口2 km纵剖面变化见图2。
由图可以看出,按照系列水沙条件运行5年,只有隧洞的进口处有所淤积,进口处的纵剖面有所变化。并且从第二年开始后,纵剖面变化不大,第一年末达到冲淤平衡。

图1 隧洞出口水位与流量关系曲线
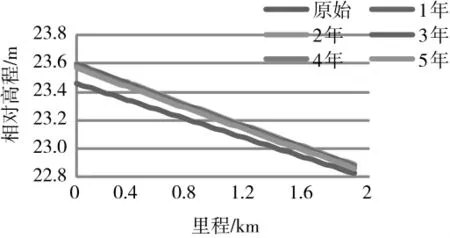
图2 距隧洞进口2 km纵剖面变化图
3.1.6 隧洞冲淤量计算结果
隧洞运行5年内,不同年限的冲淤量、累积冲淤量及排沙比等计算成果见表2。由表可以看出,隧洞运行5年内有冲有淤,淤积最大的年份是第1年,淤积量为1 246.481 m3,排沙比约为99.99%;冲刷最大的年份是第4年,冲刷量约为1 867.104 t,排沙比大于100%。隧洞运行5年整体表现为淤积,累积淤积量为761.708 m3。由此看出在此水沙系列下,淤积量很少,排沙比很大。

表2 隧洞随时间变化的冲淤量
3.2 方案二
3.2.1 计算资料
模型计算范围、时间步长以及下游边界条件同方案一。不同之处为水沙资料。
本次水沙系列5年:模拟300 d放水情况具体如图3。
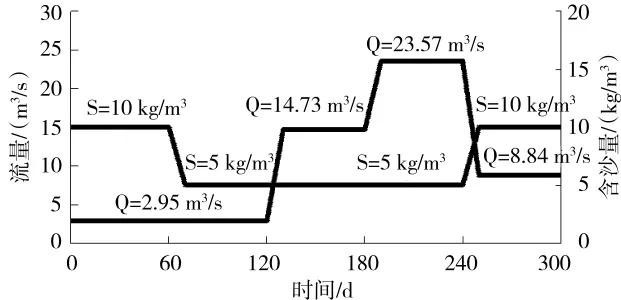
图3 300 d流量、含沙量过程线
3.2.2 隧洞纵剖面变化及对比
按照系列水沙条件计算,隧洞运行5年进口2 km纵剖面变化见图4。

图4 距隧洞进口2 km纵剖面变化图
由图可以看出,按照给定水沙条件运行5年,隧洞前半段有较大淤积,且主要集中在隧洞进口处。并且从第三年开始后,纵剖面变化不大,第四年末达到冲淤平衡。
3.2.3 隧洞冲淤量计算结果

表3 隧洞随时间变化的冲淤量
隧洞运行5年内,不同年限的冲淤量、累积冲淤量及排沙比等计算成果见表3。可以看出,隧洞运行5年内有冲有淤,淤积最大的年份是第3年,淤积量为20 249 m3,排沙比约为99.86%;冲刷最大的年份是第5年,冲刷量约为18 539 t,排沙比大于100%。隧洞运行5年整体表现为淤积,累积淤积量为15 145 m3。由此看出在此水沙系列下,淤积量较大。
4 结语
方案一计算条件下:
1)随着来水来沙条件的变化,隧洞内有冲有淤,隧洞进口段淤积厚度最大,最大淤积厚度约15.0 cm。淤积范围主要集中在隧洞进口以下2.0 km范围内。淤积厚度沿程逐渐减小。从第二年开始后,隧洞淤积纵剖面变化不大,可以认为,工程运行一年后,隧洞内即可达到冲淤平衡。
2)隧洞内累计淤积量计算结果表明,工程运行5年内,随着来水来沙条件变化,隧洞内床面泥沙有冲有淤。累计淤积量最大的年份是第1年,淤积量为1 246 m3;冲刷最大的年份是第4年,冲刷量约为1 867 t。工程运行5年末隧洞整体表现为淤积,累积淤积量为762 m3。由此看出在拟定的来水来沙条件下,隧洞内淤积量较少。
方案二计算结果表明:
1)隧洞纵剖面变化计算结果表明,随着来水来沙条件的变化,隧洞内有冲有淤,隧洞进口段淤积厚度最大,淤积厚度沿程逐渐减小。从第三年开始后,隧洞淤积纵剖面变化不大,可以认为,工程运行四年后,隧洞内即可达到冲淤平衡。
2)根据计算结果发现隧洞前半段有较大淤积,且主要集中在隧洞进口处,进口最大淤积厚度约106.8 cm。淤积范围主要集中在隧洞进口以下8.0 km范围内。
3)隧洞内累计淤积量计算结果表明,工程运行5年内,随着来水来沙条件变化,隧洞内床面泥沙有冲有淤。累计淤积最大的年份是第3年,淤积量为20249m3;冲刷最大的年份是第5年,冲刷量约为18 539 t。工程运行5年末隧洞整体表现为淤积,累积淤积量为15 145 m3。由此看出在此来水来沙条件下,隧洞内淤积量较大。
由此可见,在不同的引水引沙条件下,隧洞内的泥沙淤积情况还是有明显的区别的,所以,在实际的工程应用过程中,应该在保证隧洞内较少淤积的情况下来控制引水的条件和时段。

