EXISTENCE OF SOLUTIONS TO THE INITIAL VALUE PROBLEM OF SEMI-LINEAR GENERALIZED TRICOMI EQUATION

ZHANG Kang-qun,LI Yu-chen

(Department of Mathematics and Physics,Nanjing Institute of Technology,Nanjing 211167,China)

1 Introduction and Main Results

In this paper we study the local and global existence of solution semi-linear generalized Tricomi equation in R+×Rn,n≥2,

with the initial value

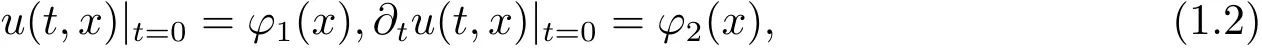
Equation(1.1)is a semi-linear hyperbolic equation with variable coeffcient and characteristic families coincide ont=0.There exist three fundamental features.First,variable coeffcient withtmakes the well known Duhamel’s principle of wave equation do not work.Then,we have to estimate the solution to the linear equation with source term.Second,its multiple characteristics cause some loss of regularities on degenerate domain.This leads tothe diffculty of local solvability.Third,the unbounded speed of propagation is an obstacle in establishing the global solution for the needed uniform decay estimate.

Form=1 andn=1,the homogeneous linear equation is the classic Tricomi equation,which was extensively investigated with suitable boundary value conditions from various viewpoints,such as[1–3]and the references therein.Forn＞1,the local existence of solution to the equation=f(t,x,u)with one initial datumu(0,x)∈Hs(Rn)was established in mixed-type domain in[4,5].Meanwhile,the propagation of weakly singularity along characteristics was studied.The low regularity solution problem of the equation with two initial data was considered in[6–7]and the positive answers were obtained.In[6],the local existence of solution was established for the given discontinuous initial data and nonlinear source term with some restrictions.In[7],the global existence and nonexistence of solutions were considered inLq(Rn)under some conditions and the decay of solutions when time trends to infinity was given.With respect to other specific cases,so far there were existence results of solution such as[8–10].In this note,we focus on the local and global existence of weak solutions to the initial value problem of semi-linear generalized Tricomi equation under some general conditions compared with the result given in[7],and establish a uniform weighted estimate in homogeneous Sobolev space

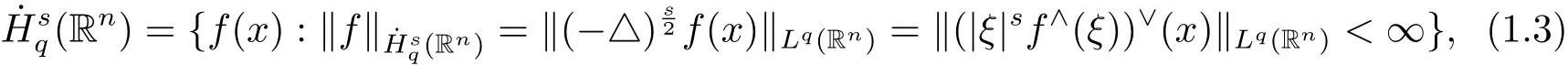
Now we state our main results.

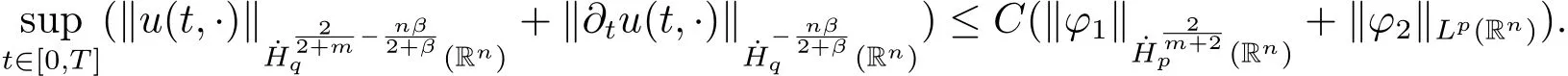
and

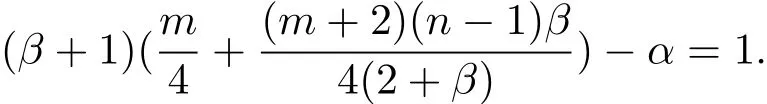
for small∈,then there eixists a unique solution

to problem(1.1),which satisfies

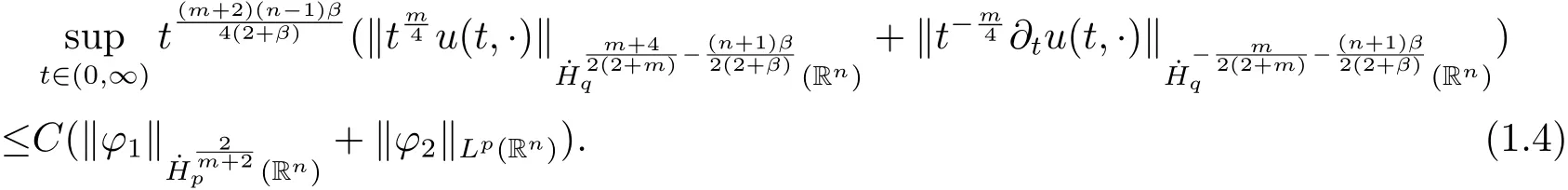
Remark 1.1 Generalized Tricomi equation has the property of“smooth effect”as we pointed out in[5].In this note,by compared with the regularity given in Theorem 1.1 and Theorem 1.2 neart=0,we note that the solution has a higher regularity away from the degenerate domain.

Remark 1.2In homogeneous Sobolev spacethe weights in the uniform estimate(1.4)of global solution in time describe the degeneracy neart=0 and the decay ast→+∞.However unlike in inhomogeneous Sobolev space[5,7],the author could not obtain those at the same time for the nonlinear problem.

Remark 1.3 In fact,the embedding theorem in homogeneous Sobolev space in page 119[11,p.119,Theorem 2]and inequality(1.4)yieldu∈C((0,∞);such that

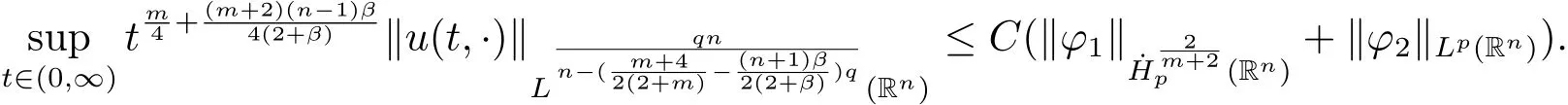
Hence,forϕ1(x)then in terms of Theorem 1.1,the conditions in Theorem 1.2 imply thatu∈C([0,∞);

This paper is organized as follows.In Section 2,for the later uses,we recite some preliminary results as our lemmas.In Section 3,by use of confluent hypergeometric functions,we derive some weighted homogeneous Sobolev regularity estimates for the corresponding inhomogeneous equation.Based on these estimates,we establish the local and global existence of solutions in Section 4 by constructing a contraction map.

2 Preliminaries

In this section,for reader’s convenience,we will recall some fundamental results of confluent hypergeometric functions and useful estimates,which will be used in Section 3 below.

The confluent hypergeometric equation iszw′(z)+(c−z)w′(z)−aw(z)=0,wherez∈C,aandcare constants.Whencis not an integer,(2.1)has one pair of linearly independent solutions

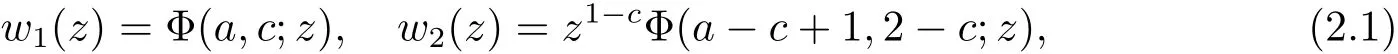
where Φ(a,c;z)is Humbert’s symbol andwiis called the confluent hypergeometric function.

The Wronskian determinant for the systemw1andw2is

Next,we list some basic properties of the confluent hypergeometric functions which can be found in[12].

Lemma 2.1 1)For−π＜argz＜πand large|z|,then

where∈=1 if Imz＞0,∈=−1 if Imz＜0,andM,N=0,1,2,3,···.2)

Then by(2.3)in Lemma 2.1,we obtain

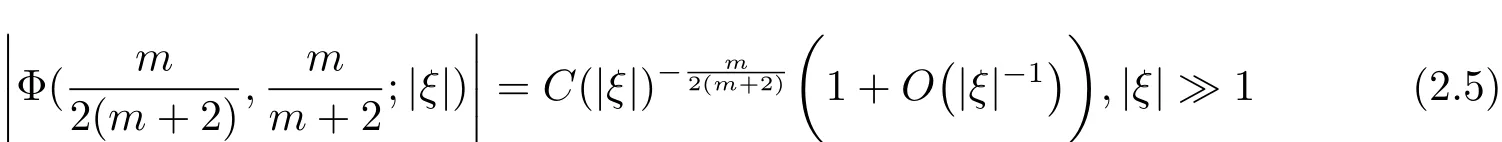
and

Next,we list Theorem 1.11 in[13]and Lemma 4 in[14]as our Lemma 2.2 and Lemma 2.3.

Lemma 2.2 Letfbe a measurable function such that,with 1＜r＜+∞,we have for some constantC,

thenf∈if 1＜p≤2≤q＜

Lemma 2.3 LetPbe real,C∞in neighborhood of the support ofv∈C∞0.Assume

that the rank ofHp(y)=∂2ykylP(y)is at leastρon the support ofv.Then for some integerM,whereCdepends on bounds of the derivatives ofPon supp(v)and on a lower bound of the maximum of the absolute values of the minors of orderρofHPon supp(v),and on supp(v).

3 Weighted Estimates of Solutions to the Linear Equation

In this section,we first take partial Fourier-transformation onx∈Rn,then the linear equation−tm△v=0 becomes

wherey(t,ξ)dxwithξ∈Rnandy′′(t,ξ)≡

Setz=|ξ|andw(z)=then ift/=0 and|ξ|/=0,the equation(3.1)can be written as

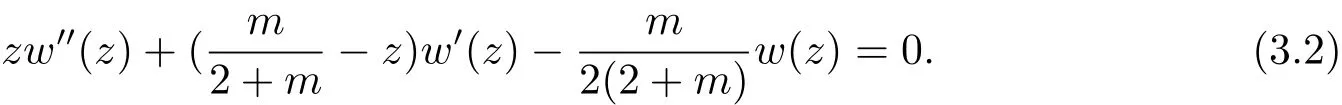
Thus(3.2)is a special case of the confluent hypergeometric equation withand

Next,we recite the result in the reference[15].

Lemma 3.1 The functions satisfy

Unlike the method of using maximum principle to solve the degenerate parabolic equation[16],here the hypergeometric functions play an important role.According to Lemma 2.1,it is easy to verify that(V1(1,|ξ|))∨and(V2(1,|ξ|))∨are two Fourier integral operators with symbols of orderThen they are bounded inLp(Rn).Moreover,the following results were obtained by taking a similar procedure in Theorem 3.1[7]in terms of some micro-local representations.

Lemma 3.2Forφ∈＞1,set 1＜p＜2 andthen

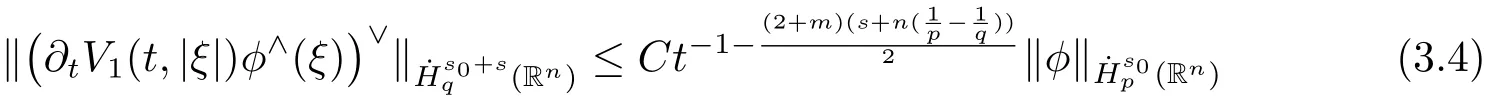
with−1

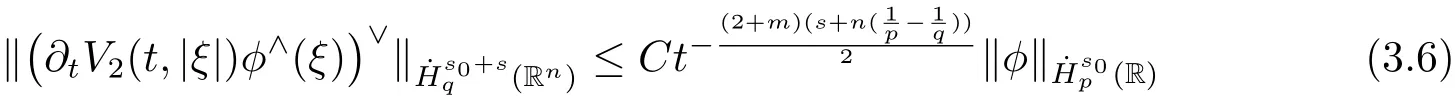
Remark 3.1 Inequalities(3.3)–(3.6)take effect forp＜2＜qandn≥2.

Next,we consider the initial value problems of homogeneous equation

As direct results of Lemma 3.1 and Lemma 3.2,we obtain the representation of distributional solution and the following estimates.

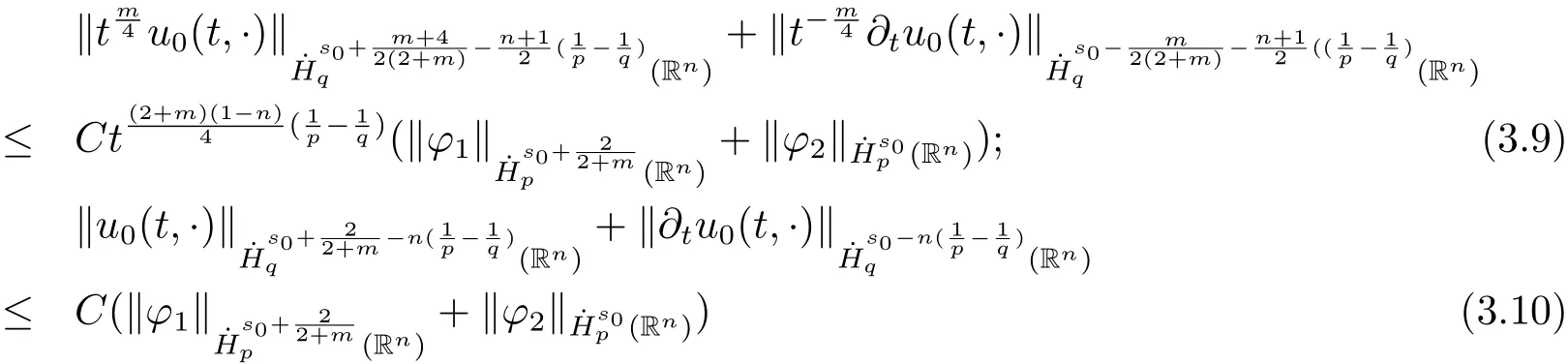
for 1＜p＜2,

Proof In terms of the representation ofu0(t,x)defined in(3.8),by use of the inequalities(3.3)–(3.6)with the value ofsfixed on the right endpoint number separately,it is easy to verify that(3.9)holds.And(3.10)can be derived by choosing the value ofswith the corresponding left endpoint number.

Last,we consider the inhomogeneous problem

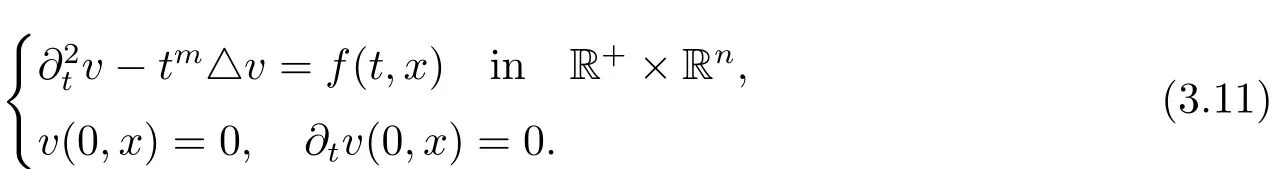
In terms of Lemma 3.1 and a direct computation with(2.2),the distribution solution of(3.11)can be expressed as

v∧(t,ξ)≡(Ef)∧(t,ξ)

Then we conclude

Lemma 3.4Iff(t,x)∈C([0,∞),then

Remark 3.2 Uniform weighted estimates of(3.9)and(3.13)give the decay rates of the solution at infinity in time.Meanwhile(3.10)and(3.14)imply the local existence with low regularity.

Proof By a direct computation,we obtain

then it is easy to verify that

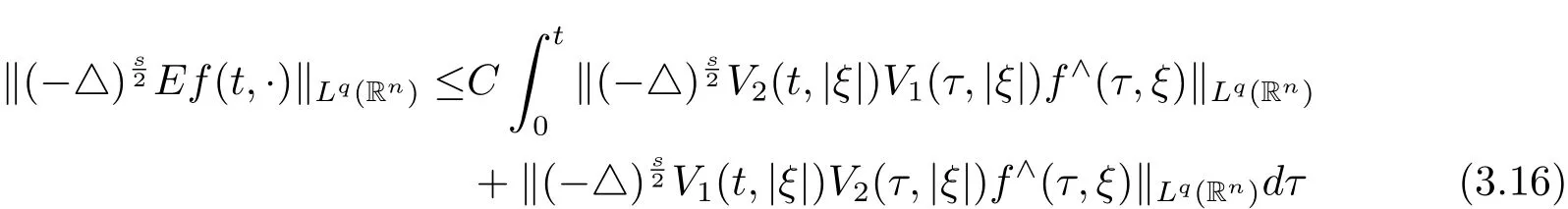
and

In terms of(2.4)in Lemma 2.1 or(3.11)–(3.12)as given in[12],we obtain∂tV1(t,ξ)=

and

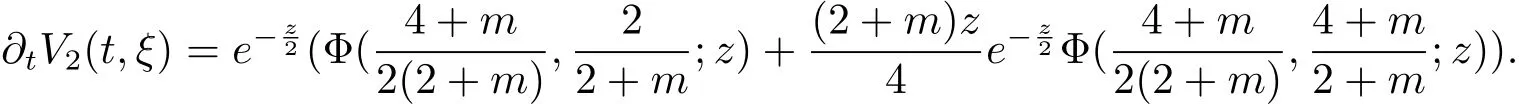
Then for the similarity of the procedure on proof of above estimate,so we only consider the termV2(t,|ξ|)V1(τ,|ξ|)f∧(τ,ξ)withτ∈(0,t).

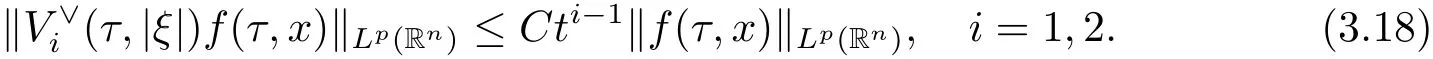
Hence,by use of(17)in Lemma 3.2,we derive

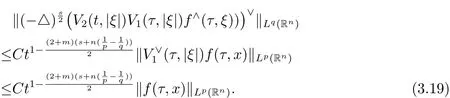
Chooses=inequality(3.19)becomes

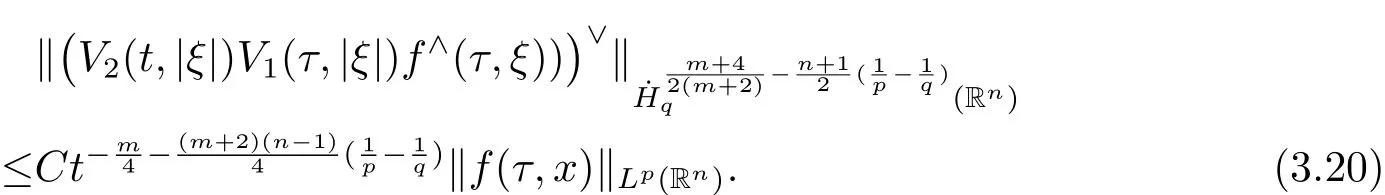
On the other hand,by a similar method,we obtain

Combining(3.17)with inequalities(3.20)–(3.21),we conclude

Then,by taking a similar procedure,we obtain(3.13)–(3.14).

4 Existence of Solutions to the Semi-Linear Problem

In this section,we construct a contraction map on a de fi ned closed set separately,then use fixed point theorem to prove the local and global existence of solution to initial value problem(1.1).

Proof of Theorem 1.1 De fine a closed set

for a constantM＞0 and the distant of elements inSM,d(u,v)

Consider the mapFdefined onSM,

whereu0is defined by(3.8)in Lemma 3.3 andE(u|u|β)is defined by(3.12)in Lemma 3.4.Setq=(β+1)p,then in terms of the embedding theorem in homogeneous Sobolev space under the conditionn−=1,we obtain

This implies thatF(u)∈SMfor smallness ofT.

This yields the contraction property of mapFonSMfor smallness ofT.

Note thatp=then in terms of(4.3)and(4.4),we establish Theorem 1.1.

Proof of Theorem 1.2 Define a closed set

S∈={u∈C((0,∞);

with the distant of elements inS∈,d(u,v)=

Consider the mapFdefined onS∈,F(u)=u0+E(tαu|u|β),whereu0is defined by(3.8)in Lemma 3.3 andE(u|u|β)is defined by(3.12)in Lemma 3.4.Setq=(β+1)p,in terms of the embedding theorem in homogeneous Sobolev space under the condition=1,we obtain

Then,in terms of the condition

this implies thatF(u)∈S∈for the smallness of∈.

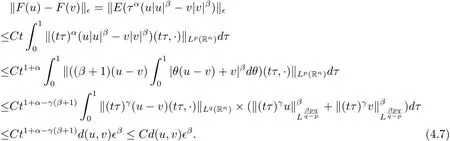
This yields the contraction property of mapFonS∈.

Finally,in terms of(4.6)–(4.7)andp=we complete the proof of Theorem 1.2.

[1]Tricomi F G.Sulle equazioni lineari alle derivate parziali di 2oordine ditipo misto[J].Atti Accad.Naz.dei Lincei,1923,15(5):133–247.

[2]Morawetz C S.Mixed equations and transonic fl ow[J].J.Hyper.Diff.Equ.,2004,1(1):1–26.

[3]Rassias J M.Mixed type partial differential equations with initial and boundary values in fl uid mechanics[J].Int.J.Appl.Math.Stat.,2008,13(J08):77–107.

[4]Beals M.Singularities due to cusp interaction in nonlinear waves[J].Nonl.Hyper.Equ.Field The.(Lake Como,1990),36–51,Pitman Res.Notes Math.Ser.,253,Harlow:Longman Sci.Tech.,1992.

[5]Zhang Kangqun.Existence and regularity of solution to the generalized Tricomi equation with a singular initial datum at a point[J].Acta Math.Sin.,2012,28(6):1135–1154.

[6]Ruan Zhuoping,Witt I,Yin Huicheng.On the existence and cusp singularity of solutions to semilinear generalized Tricomi equations with discontinuous initial data[J].Commun.Contemp.Math.,arXiv:1211.0334v1[math.AP],2012.

[7]Yagdjian K.Global existence for then-dimensional semilinear Tricomi-type equations[J].Commun.Part.Diff.Equ.,2006,31(6):907–944.

[8]Yagdjian K.The self-similar solutions of the one-dimentional semilinear Tricomi-type equations[J].J.Diff.Equ.,2007,236(1):82–115.

[9]Galstian A.Global existence for the one-dimensional second order semilinear hyperbolic equations[J].J.Math.Anal.Appl.,2008,344(1):76–98.

[10]Zhang Kangqun.A note on initial value problem for the generalized Tricomi equation in a mixedtype domain[J].Acta Math.Sin.,2013,29(8):1581–1596.

[11]Stein E M.Singular integrals and differentiability properties of functions[M].Princeton:Princeton Univ.Press,1970.

[12]Erdelyi A,Magnus W,Oberhettinger F,et al.Higher transcendental functions,vol.1[M].New York:McGraw-Hill,1953.

[13]Hormander L.Estimates for translation invariant operators inLpspaces[J].Acta Math.,1960,104(1):93–140.

[14]Brenner P.OnLp−Lqestimates for the wave equation[J].Math.Zeitschrift,1975,145(3):251–254.

[15]Taniguchi K,Tozaki Y.A hyperbolic equation with double characteristics which has a solution with branching singularities[J].Math.Japon.,1980,25(3):279–300.

[16]Li Mei,Xie Chunhong.Global existence and blow-up of solutions for degenerate parabolic systems[J].J.Math.,2004,24(2),197–203.