基于反馈迭代和独立分量分析的多次波压制技术研究❋

常 青， 徐秀刚， 孙道朋

(海底科学与探测技术教育部重点实验室，中国海洋大学海洋地球科学学院，山东 青岛 266100)

多次波是一种规则干扰波，在海洋地震勘探的资料处理中普遍存在多次波的问题[1]。多次波处理不当会混淆、干扰有效波成像，出现多次波同相轴掩盖有效波同相轴的情况，在很大程度上干扰地震资料的偏移成像效果[2]，甚至会导致对地震资料解释和地下构造的错误认识，影响着探井井位的部署和勘探的成功率。

多次波压制方法分为基于有效波和多次波的特征差异的滤波方法和基于波动方程的预测减去法[3]。当有效波和多次波时差较大时，滤波方法能够很好地压制多次波，但是当有效波和多次波的特征差异较小时，该方法则会损伤有效波。基于波动方程的预测减去法却能很好的处理这种情况，该方法是数据驱动的，在不需要速度模型等先验信息下，就能够处理地下介质较复杂时的多次波与有效波的分离[4-5]。

最初，Anstey等[6]利用单道的自相关压制自由表面多次波。Kennett[7]提出一维表面多次波的正演和反演模拟方法，但是由于该方法对于数据需要做许多假设，不能成功应用于实际资料的多次波压制。后来，荷兰Delft大学的Berkhout[8]提出反馈模型和数据矩阵的概念，奠定了反馈迭代法预测多次波的基础。由于该方法是是利用叠前地震数据预测自由表面多次波，无需地下介质的任何信息，受到众多地球物理学家们的关注。

常规的多次波压制技术是基于输出信号能量最小准则进行匹配相减的[9]，这一准则不能很好的处理有效波和多次波非正交的情况下的多次波压制，而实际地震数据基本不满足多次波和有效波是正交的(两个波形不重叠且其相位差为90°)。近年来，许多学者将ICA(Independent Component Analysis，独立分量分析法)算法运用到地球物理中，实现对于非正交数据的处理。刘喜武等[10]提出利用ICA方法实现地震转换波与多次反射波的分离，陆文凯等将ICA方法用于多次波的压制中并提出“几何独立分量分析方法”[11-12]，Kaplan等[13]也将ICA思想应用于多次波的分离中并取得理想的压制结果。

为避免压制效果受速度模型、地层信息等先验信息的影响，本文借鉴了预测减去法的思路，采用基于波动方程的反馈迭代法实现对于自由表面多次波的预测，然后基于高阶统计量的快速ICA算法实现多次波与有效波的匹配相减，完成最终的自由表面多次波压制。本文压制方法完全是数据驱动的，而且克服了常规匹配算法对于有效波和多次波非正交情况不能很好压制多次波的缺陷，实现了对于自由表面多次波的良好压制。资料试算的结果，验证了本文方法压制多次波的正确性，有效性和实用性。

1 基于反馈迭代和独立分量分析的多次波压制

1.1 反馈迭代预测多次波的原理

基于波动方程的反馈迭代预测多次波方法不需要地下地层的介质信息，可以直接由地震数据本身预测自由表面多次波。地震数据本身被用作波场延拓算子，通过对其进行多维褶积运算，有效波变成一阶多次波，一阶多次波变成更高阶多次波，该方法通过数据驱动，可以直接利用叠前地震数据构建表面多次波，无需地下介质的信息。

在多次波预测中，引入了波场延拓的思想，波场延拓过程中，格林函数表述了延拓路径。在表面多次波预测中，一次波的脉冲响应函数X0将作为格林函数预测所有可能的多次波。在二维多次波预测中，采用Rayleigh积分的非稳态空间褶积表示形式，即表面多次波M0(xr,xs,f)的预测写成公式(1)所示的空间褶积的积分形式：

M0(xr,xs,f)=

(1)

式中：xs为炮点位置；xr为检波点位置；xk为求和所进行的横向坐标；X0(xr,xk,f)为无表面多次波的脉冲响应。

写成离散求和形式如下：

M0(xr,xs,f)=

(2)

如果对所有的炮点和检波点组合重复该过程，则多次波的预测可表示成矩阵乘法形式：

M0=-X0P。

(3)

M0(xr,xs,f)=

(4)

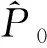
写成矩阵乘法形式：

(5)

多次波迭代预测多次波方法可表述为：

(6)

(7)

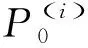
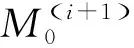
1.2 基于独立分量分析方法的多次波剔除

在多次波预测减去法中，多次波相减是最为关键的一环，利用不同的数学方法来获得自适应参数，使得预测的多次波在匹配处理后与实际地震数据中的多次波尽可能的一致，然后再从实际的地震数据中将多次波减去，从而得到有效波的信息。

独立分量分析方法是近二十年发展起来的一种高效盲信号分离方法。它的基本思想是从一组观测到的混合信号中恢复无法直接观测到的独立原始信号，其用一些基函数来表示一系列的随机变量并且假设各成分之间是统计独立的或者尽可能的独立。其最简单的形式是：给定N个观测信号x1,x2,…,xn,假设它们为n个未知的统计独立的源信号s1,s2,…,sn的线性组合：

xj=aj1s1+aj2s2+…+ajnsn,j=1,2,…,n。

(8)

式中aj1,aj2,…,ajn为输入观测量的线性组合系数。

写成矩阵形式如下：

X=AS。

(9)

设观测到的地震信号为X，由一次波P和多次波M组成，则有：

X=P+M。

(10)

设通过多次波预测技术得预测的多次波为Mp，为了消除Mp和实际地震数据中的多次波M之间的不同子波因素，采用了基于最小能量的子波估计方法[14]，用如下的子波校正滤波器进行子波的校正：

(11)

式中：W(ω)是一个一维窗函数；上标*表示复数共扼；⊗表示褶积运算。

利用该子波校正滤波器，得到子波校正后的预测多次波：

(12)

设子波因素消除后的近似多次波为：

Mp=αM。

(13)

式中：α为尺度系数。

压制地震信号X中的多次波所用的常规的基于二阶统计量能量函数的方法是最小化如下的函数：

(14)

上式对应的最小二乘解为：

(15)

考虑到峰度对信号中的大值的敏感性较高，采用了如下的对数范数度量[9]：

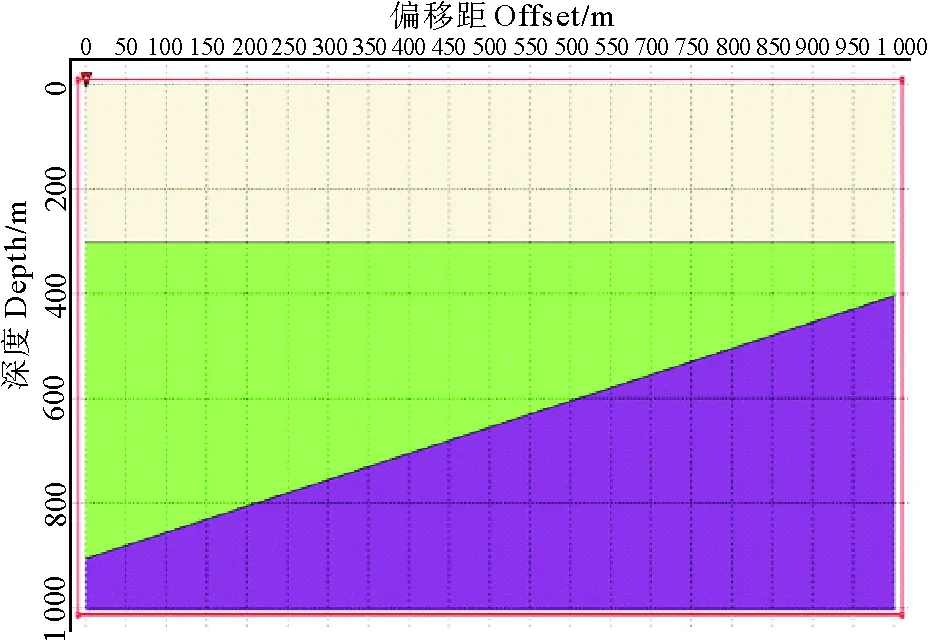
图1 倾斜模型速度场Fig.1 Velocity field of the tilt model

(16)

上式中：N是信号的采样长度；qi是对应信号y的振幅归一化信号，即：

(17)

ICA就是通过最大化高阶统计量的能量函数：

(18)

来实现多次波的自适应相减。

2 数值模型试算

为验证本文方法的多次波压制效果，本文通过倾斜层模型以及Sigsbee2B模型分析等实现了对于该方法技术的试算，通过资料试算，验证了方法的正确性、适应性和有效性。

本文采用的第一个模型是倾斜模型，大小为2 000 m×1 200 m，水平界面深度300 m，倾斜界面左端点深度960 m，右侧430 m，如图1所示，表层速度是渐变的，第一层为1 500 m/s，第二层为2 000 m/s，第三层为2 500 m/s。炮记录采用左边放炮的激发方式，共计96炮，每炮96道接收，每道1 000个采样点，采样率为2 ms，子波主频40 Hz。采样反馈迭代法和ICA匹配相结合的方法对该炮记录进行试算，第1炮单炮记录多次波压制结果如图2所示。

图2(a)为原始地震记录(箭头所指部分为多次波)，图2(b)是利用基于波动方程的反馈迭代方法预测的多次波。图2(c)是利用基于二阶统计量的常规匹配方法压制多次波后的地震记录，可以看到在有效波和多次波非正交部分，多次波仍然有部分残留；图2(d)是利用基于高阶统计量的ICA方法压制多次波后的地震记录，对比图2(c)可知，利用基于高阶统计量的ICA方法对于有效波和多次波非正交部分压制效果要明显优于二阶统计量的常规方法。

图2 原始地震记录与不同方法下的多次波压制结果对比Fig.2 Comparison between original record and suppressed result of multiples based on different ways

为了测试方法对于复杂构造的适应性，本文还采用国际上常用的检测多次波压制效果的Sigsbee2B模型对算法进行了测试。该模型的参数为：纵向共有1 201个采样点，采样间隔为7.62 m；纵向共有2 133个采样点，采样间隔为11.43 m。该模型的正演炮记录共有500炮，为了计算起来更加方便，本文仅抽取其中的348炮、每炮174道、每道1 500个采样点、8 ms采样进行多次波压制的实验。Sigsbee2B模型速度场如图3所示，该模型表层模拟海水层，中间是由许多正断层和逆冲断层组成的沉积地层以及埋藏在沉积地层中的一个高速度的岩丘体，可以看出该地质构造非常复杂。

该模型的正演炮记录总共有12 s，为了使得显示效果清晰便于对比，本文选取其中的第51炮并截取其中的3.2～12 s进行显示对比。

图3 Sigsbee2B模型速度场Fig.3 Velocity field of the Sigsbee2B model

图4(a)中箭头所指部分为多次波，图4(b)为利用基于波动方程的反馈迭代方法预测的多次波，比较两图可以看出，原始数据中的多次波被很好地预测出来。图5(a)为利用基于二阶统计量的常规匹配方法压制多次波后的地震记录，图5(b)为利用基于高阶统计量的独立分量分析自适应匹配方法法压制多次波后的地震记录。对比两图中方框部分可以看出，对于有效波和多次波非正交部分以及深层多次波，后者的压制效果要明显好于前者。

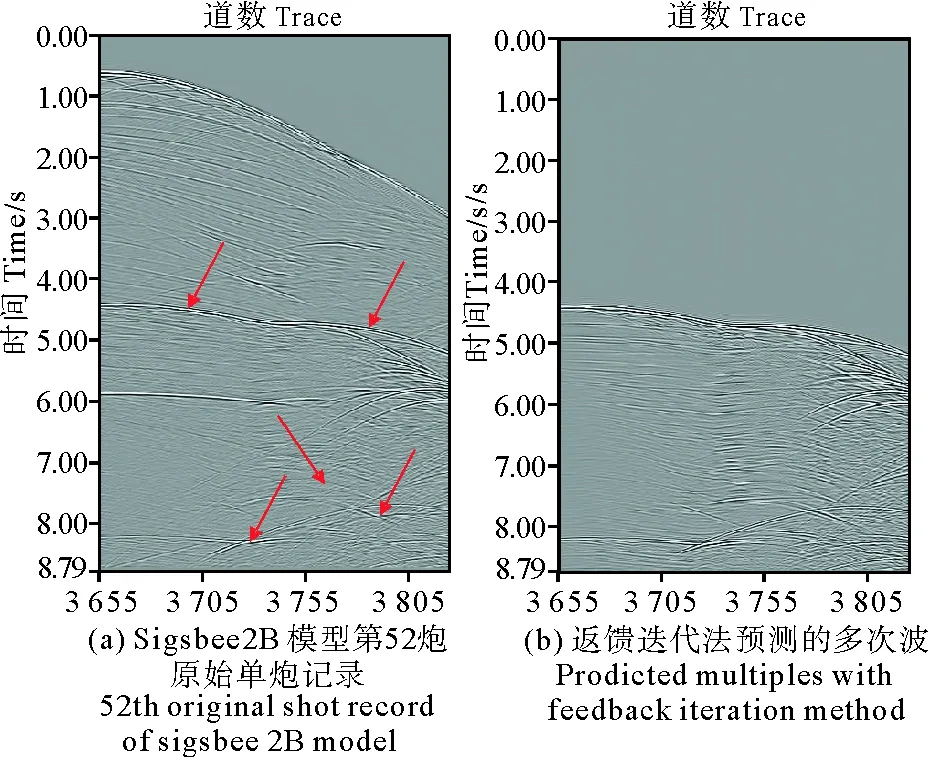
图4 原始单炮记录和反馈迭代法预测的多次波Fig.4 Original record and predicted multiples based on feedback iteration method

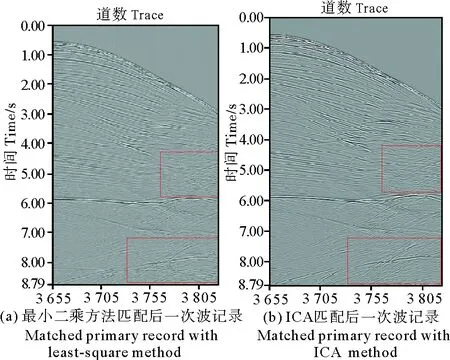
图5 基于最小二乘和ICA方法匹配后的一次波记录Fig.5 Matched primary wave record based on least-square method and ICA method

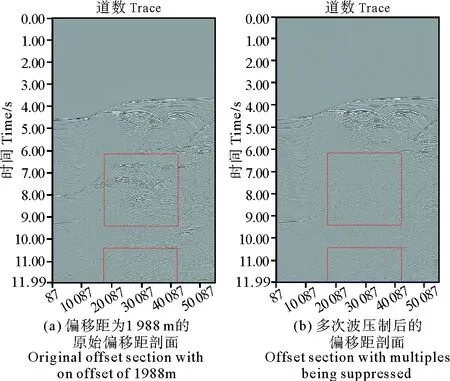
图6 多次波压制前后的偏移距剖面Fig.6 The offset section before and after multiples being suppressed

3 结论与认识

本文实现了基于反馈迭代技术和基于高阶统计量的独立分量分析技术的结合，更好的对于自由表面多次波进行了压制，取得的结论与认识是：

(1)反馈迭代法是基于数据驱动的多次波压制方法，可以直接利用叠前地震数据预测表面多次波。由于该方法不需要地层的信息，因此可对复杂地下的表面多次波进行预测。

(2)将独立分量分析技术应用于多次波的匹配压制，克服了常规匹配算法对于有效波和多次波非正交情况不能很好压制多次波的缺陷，实现了对于自由表面多次波的有效压制。倾斜模型和Sigsbee2B模型等模型资料的处理分析表明，本文方法既能够有效保持地震记录中的有效波能量，还能够实现对于自由表面多次波，特别是中、深层多次波的有效压制。