断面法与TIN法在计算矿产资源储量中的对比讨论

张 钊，郭 鹏，邓宇涛

(中煤地质工程总公司，北京 100040)

随着中国经济由高速增长阶段转向高质量发展阶段，矿产资源勘查开发面临转型升级的必然要求，如何提高勘查效率，如何节约资源，引入新技术新方法便成为矿产勘查工作的必然选择。

矿产资源勘查开发过程中，储量计算一直是重要一环，而矿产资源储量传统计算方法中使用最广泛的是断面法。但是随着地理信息技术的兴起，越来越多的计算方法被应用于实际生产，其中TIN法就是用于储量计算的方法之一。

因此，本文主要针对断面法和TIN法的计算方法和优缺点进行对比分析，为储量计算方法提供参考。

1 断面法和TIN法的计算方法

1.1 断面法

在已勘查的矿床中，当矿体被一系列勘查断面横切截为若干块段，估算相邻两断面间的矿块储量乃至整个矿体的储量，这种方法称之为断面法[1]。其体积计算公式如下：

(1)当相邻断面的矿体形状相似，且其相对面积差[(S1-S2)/S1]小于40%时，用梯形体公式：

(2)当相邻断面面积差大于40%时，用截锥体公式：

(3)当有一断面尖灭时，根据矿体尖灭特点选择不同的公式。

a.当矿体作楔形尖灭时，体积使用楔形公式计算：

b.当矿体作锥形尖灭时，体积可用锥形公式计算：

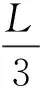
以上公式中：V为断面间矿体体积；L为相邻断面间距离；S1、S2、S为断面上矿体面积。

1.2 TIN法

不规则三角网(TIN)是数字高程模型DEM的表现形式之一, TIN法是直接利用实测地形构建三角网,以边长灵活的空间三角形去逼近实际地形, 对计算区域按三棱柱法计算体积[2]。

利用ArcGIS 软件，通过矿体开采前后的数字高程模型对比计算出开采的体积。为了满足精度要求，把开采区划分成尽量多的子区域，每个子区域在开采前后地表高程降低或抬高的差值乘以该子区域面积，即为该子区域的体积，所有子区域的体积分别累加即为总体积方量[3]。计算公式为：

式中：Ai为第i个子区域面积;Hi为第i个子区域开采前高程;hi为第i个子区域开采后高程;n为子区域数量;i为当前计算子区域编号;V为体积。

各个子区的划分由ArcGIS软件自动划分，具体操作方法如下：

(1)导入RTK数据到ArcGIS(图1)；

图1 RTK采集点位图Figure 1 RTK sampling points

(2)矢量数据生成TIN，构建三维地表模型(图2)；

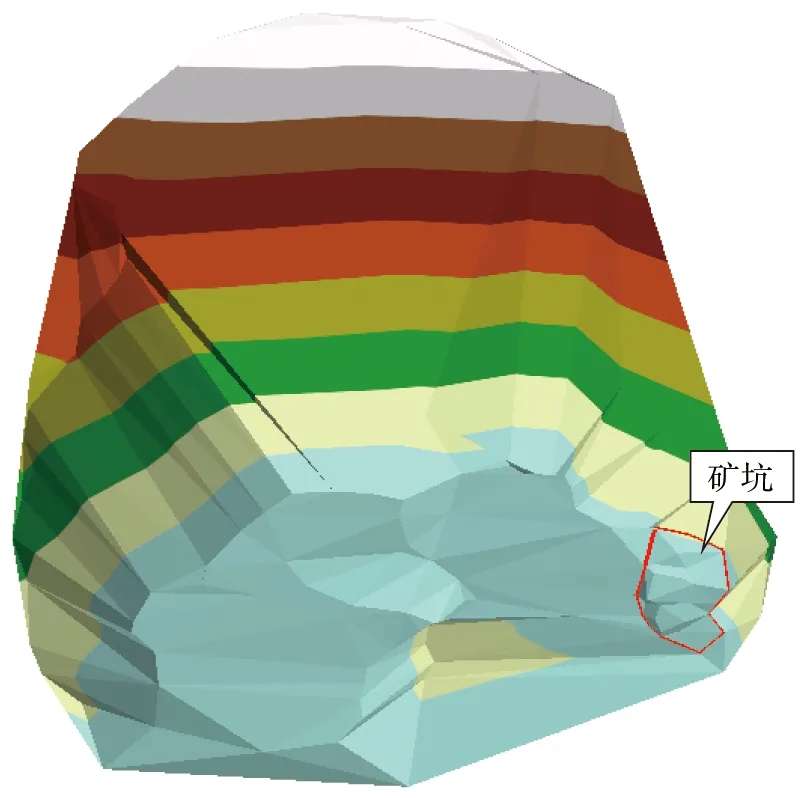
图2 矿区现状三维模型图Figure 2 3D model of mine area status quo

(3)ArcGIS的工具箱中，选择三维分析工具，再选择表面模型计算中的挖填方。分别输入矿体开采前的TIN和矿体开采后的TIN，自动计算后会生成一个文件，打开文件的属性表就可以查看体积信息，表中的VOLUME字段代表的就是体积，AREA字段则是代表勘查投影面积；

(4)使用ArcScene则可实现矿体的三维可视化(图3)。

图3 矿体三维模型图Figure 3 3D model of orebody

2 两种方法的优缺点对比

2.1 适用范围对比

断面法作为传统的矿产资源储量计算方法，具有其勘查的广泛适用性。无论是露天开采还是地下开采，均可使用断面法计算资源储量。而且较少受到矿产类型的限制。

TIN法受限于数据采集的要求，数字高程模型格网间距依据不同比例尺有不同的精度要求，所以数据采集一般是使用RTK完成，因此主要应用于露天开采的矿产资源。而且，一般用来计算测量范围内比较单一的矿产资源。当一个矿区内有多种矿产，或者矿体类型较为复杂无法直接采集数据时，单纯使用TIN法难以完成储量计算的任务。

2.2 精度对比

断面法在使用过程中，仅依据面积差[(S1-S2)/S1]以40%为界限，而不根据实际的矿体形状选择使用公式时，很容易产生误差，例如在该用梯形公式计算时而用了截锥公式, 最大相对误差可达33.3%[4]。另外在地形变化较大的区域，依靠断面法计算会人为的将实际地形变为标准几何图形而忽略其变化，测算结果有一定出入。

TIN法是使用空间三角形去逼近实际地形，因此完全不受地形变化的限制，并且贴合程度更高。其精度仅与基础数据有关，较之断面法有明显的优势。

2.3 效率对比

断面法依靠技术人员现场勘查完成地质剖面的绘制，再计算断面的面积，最后依据断面和矿体形态选择公式完成计算，基本依靠地质人员完成所有工作，自动化程度低。

TIN法仅需要现场采集数据，使用ArcGIS软件完成体积计算，简单、快速, 自动化程度高,并且实现了土方的可视化，效率远远超过断面法。

3 结论

综上所述，在露天矿体的开采储量计算方面，TIN法无疑更占优势，比断面法更加精准、更加高效，而且能够不受地形起伏的影响。而断面法的优势在于，适用范围更广，无论是地下开采还是不同矿种类型都可使用。建议根据工作面临的实际情况选择使用最适合的工作方法。

[1]李守义，叶松青.矿产勘查学(第二版)[M].北京:地质出版社, 2003.

[2]李春梅，景海涛.基于ArcGIS 的土方量计算及可视化[J].测绘科学，2010，35(2):186-187.

[3]张建成,葛亮,王亮.利用ArcGIS进行土方挖填方量计算的原理与实践[J].中国水土保持,2016,(07):65-67.

[4]袁崎.储量计算中平行断面法公式的使用条件[J].地质与勘探,1984,(12):42-48.