变压器结构性故障群决策诊断
江保锋,窦建中,熊 玮
(国网华中电力调控分中心,湖北 武汉 430077)
0 引言
结构性故障是导致电力变压器发生损坏事故的主要原因之一[1-4]。对运输或接受短路冲击后的变压器进行结构性故障诊断可确保变压器的安全稳定运行。目前常用的变压器结构性故障离线检测方法主要有频率响应法(Frequency Response Analysis,FRA)、短路阻抗法(Short Circuit Impedance Method,SCI)及电容法(Capacitance Method,C)等[2-4]。大量现场试验表明,受现场测量精度和故障诊断判据的限制,应用单一检测方法难以准确反映变压器的结构性故障,且各种方法可能得到有分歧的诊断结果。针对单一检测结果的不确定性和局限性,综合多种检测方法的变压器结构性故障多属性诊断并以概率来表征各种故障出现的可能性能提高诊断结果的合理性。
由于现场试验条件、变压器结构型式的差异等,目前各种检测方法的检测判据未能获得一致认同,现场的结构性故障诊断主要依赖于检测者的经验判断。由于检测方法的不确定性和专家的主观性,不同决策者(专家)的结论往往存在分歧。不同的决策者所拥有的知识和经验往往是有限的、片面的,因而需要将不同相关知识领域专家的意见综合起来,使评估结果更为准确。在变压器在线状态监测评估中,粗糙集理论[5]、贝叶斯网络[6-7]、模糊理论[8]、支持向量机[9-10]、证据推理法理论[11]等方法被广泛用来融合多种检测结果,建立相应的专家诊断系统。其中证据理论在综合多个决策者的意见时,通过应用证据理论的合成法则可得到较满意的结果。随着证据理论的发展,证据理论在群决策领域中应用日益广泛。为更好地诊断变压器的结构性故障,本文在综合多种检测方法的基础上,提出基于证据推理的群决策方法对多位决策者的判断结果进行融合,在多种决策存在分歧、关键数据缺失、数据冗余等情况下得到变压器所处状态的最大可能概率。
1 变压器结构性故障群决策诊断模型
变压器可认为由有限个电阻、电容、电感等分布参数元件组成的复杂网络,当发生结构性故障时,这些参数随着故障类型的不同发生相应改变。现场试验常采用频率响应法、短路阻抗法、电容量法测量相应特征参数变化评价变压器的结构状态。典型的证据推理模型包括决策层、评价等级层、因素层。本文综合这三种常用的结构性故障诊断方法,构建了两级结构的群决策模型,如图1所示。其中群决策y是对变压器状态的综合评价,是结合多条个体决策得出的综合诊断。评价等级层中HN为变压器状态对应的不同评价等级,对应于变压器的不同状态。根据实际运行经验及变压器典型故障类型[12-15],本文定义变压器的7种可能状态为:
H={H1,H2,H3,H4,H5,H6,H7}={正常,匝间短路,夹件失压,轴向位移,挂环抱箍翘曲,剩磁,不良接地}

图1 变压器故障群决策模型Fig.1 GMADM model of transformer
yM为不同决策者所得做出的个体决策。受不同决策者经验所限,个体决策可能会针对不同侧重点,因此需要考虑各决策者的的相对权重,将个体决策进行合成,以减小决策者的主观因素影响,提高诊断准确性。
基本因素层中eLL对应于各决策者所采用的不同诊断方法、具体检测方式、比较方法、判据等。
2 证据推理合成法则
典型的证据推理模型[13,16-18],包括决策层y、评价等级层H,基本因素层E。
令模型中的评价等级为

令模型中的基本因素为

对基本因素ei,其对于决策y的相对重要性用权重ωi(0≤ωi≤1)表示。因此得到权重矩阵

证据推理合成法则是一种多属性决策算法,具体步骤如下。
(1)基本因素ei的影响
定义βn,i为基本因素ei对于评价等级Hn提供的确定度,易得βn,i≥0且,则基本因素ei的总体影响为

(2)基本概率值mn,i
mn,i为基本因素ei的权重(即其对于决策y的相对重要性)与基本因素ei对于评价等级Hn提供的确定度的乘积,表示基本因素ei支持决策y为评价等级Hn的基本概率。

由于基本因素ei存在不完整的可能性,上式并不能完整表述整个概率空间。相应地,定义未指定的剩余概率为

(3)迭代计算
定义mn,I(i)为前i个基本因素支持决策y为评价等级Hn的基本概率之和,为对应的剩余概率。通过以下迭代公式可以求出任意i对应的基本概率之和。
迭代初始条件为

确定迭代初值后,将初始值带入式(10)~(13),逐步迭代后续数据。

式中

(4)归一化
定义βn为基本因素层E对于评价等级Hn提供的确定度,通过对基本概率值的归一化可以求出βn。

则基本因素层E对决策y的总体评价为

3 群决策综合诊断
群决策主要研究群体的共同抉择,即在个体决策偏好的基础上,构造群体偏好关系,进行综合决策[19-20](见图2)。群决策与个体决策有着本质的区别,群决策具有以下两个特点:
(l)群决策中的个体决策者由于知识背景、经验和获取信息等不同,在选择决策方案时产生不同的理解,因此可能存在不同的偏好。群决策结果依赖于不同个体决策者的偏好,不同个体决策有时候可能差别较大,甚至相反。在对不同决策者给出的结论进行处理和合成时,可能造成的冲突,产生与直觉相悖的结论。
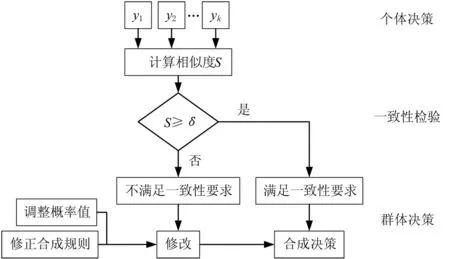
图2 群决策框图Fig.2 Framework of GMADA
(2)为了把多个决策者的意见形成一个统一的决策方案,需要将不同的个体决策进行一致性检验。首先引入相似度的概念S(βi,βj),并预先定义一个阈值δ,然后计算不同决策者对任意两个评级等级所得概率之间的相似度。若S(βi,βj)≥δ,则认为个体决策者的意见是一致的;若S(βi,βj)<δ,则说明个体决策者的意见不满足一致性要求。对满足一致性条件的个体决策进行合成,得到群决策的最终结果。
将每个决策者所得决策yi(i=1,2,…,M)看成一个长度为N的行向量,其中N为评价等级数,即变压器的可能状态个数。

决策 yi,yj之间任意两个评价等级的概率βi,βj之间的距离定义为

式中:βi,βj分别为yi,yj中的元素;表征决策 yi,yj之间的相似程度,对于确定的 yi,yj易知Dij为确定值。
Dij满足以下三个条件:(1)Dij∈[ ]0,1,当且仅当yi=yj时,Dij=1 ;(2)当 yi,yj所得出的结论趋近于相同时,Dij∈[ ]0,1 趋近于 1;(3)当 yi,yj所得出的结论趋近于不同时,Dij∈[ ]0,1趋近于0。
定义不同个体决策yi,yj中任意两个评价等级的概率βi,βj之间的相似程度[21]为

显然,S(βi,βj)越大,则两个概率值βi,βj之间的距离d(βi,βj)越小,其相似程度越高,即个体决策者的意见差别越小,二者的一致性越高;反之,S(βi,βj)越小,则距离越大,差别越大,一致性越低。
对于一致性较低的两个个体决策,在合成过程中有两种解决策略[22]:一是修改个体决策。在个体决策高度冲突时,各决策者应该进行沟通与交流后,对给出决策的合理性进行讨论,必要时对所做决策进行修正。
另一种是建立基于相对可靠度的决策合成规则。不同决策者的权威性、知识、经验不完全相同,因此,在群体中不同决策者针对不同问题的决策可靠程度也不一样。若某条个体决策被其他的个体决策所支持,则该个体决策具有较高可信度,其权重也应该较大;反之若某条个体决策与其他个体决策的冲突都比较大,则该个体决策具有较低可信度,相应的该个体决策对应的权重也较低,其对最终合成的结论的影响也较小。
假设有M个决策者,对应的个体决策为y1,y2,…,yM,则由这M条个体决策所组成的系统对个体决策yi的支持程度为

个体决策yi的可信度为

可信度Crd(yi)可以作为个体决策yi的权重,在获得各条个体决策的权重后,对其进行加权平均,即可求得归一化的权重。
若个体决策yv满足

则yv为N条个体决策的代表性决策,获得权重最大。
在基于相对可靠度的决策合成规则中,通过权重来衡量评判结果的可信度,在决策之间冲突较大时,应该有限考虑权重较高的个体决策。因此合成法则主要有以下三种修正方式:(1)由于代表性决策具有最大的权重及最高的重要性,可以考虑将代表性决策合成M-1次,并将合成的结果作为最终结果;(2)可以考虑去掉权重最小的几条个体决策,仅由其余权重较高决策者所给出的个体决策进行合成;(3)分别计算M条个体决策两两之间的支持度Sup(yi)和可信度Crd(yi),将计算得到的各条个体决策的权重,带入基本概率值m的计算过程中,进行加权平均,计算出新的个体决策。
通过以上方法对现有合成方法进行改进,同时结合对个体决策中基本概率值的修改,即可达到群决策过程中解决个体决策冲突的目的。
4 算例分析
选取一组典型试验数据作为算例,假设三位个体决策者所得出结论为:
y1={(正常,0.60),(不良接地,0.20)};
y2={(正常,0.75),(匝间短路,0.10)};
y3={(正常,0.50),(轴向位移,0.10),(剩磁,0.15),(不良接地,0.20)}
易求出个体决策两两之间的Dij为:
D12=D21=1/3;
D13=D31=2/4;
D23=D32=1/5
只考虑相同评级等级之间的相似程度,即对角矩阵上的元素,求出个体决策y1与y2之间评价等级间的距离

同理,求出各条个体决策的评级等级之间的相似度如表1所示。选取相似程度阈值δ=0.9(经验值),则由表1可以确定:个体决策y1与y2对于变压器处于“不良接地”状态的判断相似程度较低;个体决策y1与y3对于变压器处于“剩磁”状态的判断相似程度较低;个体决策y2与y3对于变压器处于“正常”状态的判断相似程度较低。由于个体决策已经确定,各决策者无法进行沟通与交流,需要对合成的权重进行修改,建立基于相对可靠度的决策意见合成规则。

表1 个体决策间相似程度Tab.1 Similarity between single decisions
分别求出三条个体决策对应的支持程度、可信度如表2所示。

表2 个体决策可信度Tab.2 Reliability of single decisions
确定 y1、y2、y3的对应权重为ω1=0.338 7、ω22=0.258 1、ω23=0.403 2。分别计算出个体决策yi支持群决策y为评价等级Hn的基本概率值、剩余概率值,并经迭代计算后得出归一化概率,如表3所示。

表3 基本概率值、剩余概率值及归一化概率Tab.3 Basic probability mass,remaining probability mass and normalization probability mass
按照基于相对可靠度的决策合成规则得出群决策的判断:
y={(正常,0.655 6),(匝间短路,0.019 4),(轴向位移,0.038 3),(剩磁,0.057 5),(不良接地,0.153 6)}。
通过群决策判断变压器有65.56%的概率为正常,1.94%的概率为匝间短路,3.83%的概率为轴向位移,5.75%的概率为剩磁,15.36%的概率为不良接地。
群决策的结果减小了相似程度较低的判断的概率,在计算过程中表现为减小相似度较低决策的权重,增加相似度较高决策的权重,如个体决策y1与y2对于变压器处于“正常”状态的判断相似程度较高,因此认为变压器处于“正常”状态的概率在60%~75%的权重较大,在最终的群决策中变压器有65.56%的概率为“正常”。对应仅在少数个体决策中出现的判断,其可信度较低,在最终群决策中的概率将减小,如个体决策y2中的“匝间短路”,个体决策y3中的“轴向位移”“剩磁”等状态。
5 结论
(1)由于检测方法的不确定性和专家的主观性,不同决策者(专家)对于变压器的结构性故障诊断往往存在分歧。群决策能够将权威性、知识、经验不完全相同的个体决策者的判断按照一定的偏好进行合成,能够在多种决策存在分歧、关键数据缺失、数据冗余等情况下得到变压器所处状态的最大可能概率。
(2)本文引入个体决策之间相似度与可信度的概念,建立了基于相对可靠度的决策意见合成规则,能够克服单一决策者的局限,解决不同个体决策存在冲突情况下的综合诊断问题。
(3)通过对算例的分析计算,群决策能明显减小不可靠个体决策的影响,验证了本文提出的群决策方法在变压器结构性故障诊断方面的可行性。
[1] CHRISTIAN J,FESER K.Procedures for detecting winding displacements in power transformers by the transfer function method[J].IEEE Transactions on Power Delivery,2004,19(1):214-220.
[2] PRAMANIK S,SATISH L.Estimation of series capacitance for a three-phase transformer winding from its measured frequency response[J].IEEE Transactions on Power Delivery,2013,28(4):2437-2444.
[3]PALANI A,SANTHI S,GOPALAKRISHNA S,et al.Real-time techniques to measure winding displacement in transformers during short-circuit tests[J].IEEE Transactions on Power Delivery,2008,23(2):726-732.
[4] JOSHI P M,BADGUJAR K,KULKARNI S V.Localization of deformations in transformer windings using terminal capacitance measurements[C]//IEEE 1st International Conference on Condition Assessment Techniques in Electrical Systems,2013:318-324.
[5] 莫娟,王雪.基于粗糙集理论的电力变压器故障诊断方法[J].中国电机工程学报,2004,24(7):162-167.MO Juan,WANG Xue.Diagnostic model of insulation faults in power equipment based on rough set theory[J].Proceedings of the CSEE,2004,24(7):162-167.
[6] 朱永利,吴立增,李雪玉.贝叶斯分类器与粗糙集相结合的变压器综合故障诊断[J].中国电机工程学报,2005,25(10):159-165.ZHU Yongli,WU Lizeng,LI Xueyu.Synthesized diagnosis on transformer faults based on Bayesian classifier and rough set[J].Proceedings of the CSEE,2005,25(10):159-165.
[7] 王永强,律方成,李和明.基于粗糙集理论和贝叶斯网络的电力变压器故障诊断方法[J].中国电机工程学报,2006,26(8):137-141.WANG Yongqiang, LÜ Fangcheng, LI Heming.Transformer fault diagnosis method of power transformer based on rough set theory and Bayesian net work[J].Proceedings of the CSEE,2006,26(8):137-141.
[8] 廖瑞金,王谦,骆思佳,等.基于模糊综合评判的电力变压器运行状态评估模型[J].电力系统自动化,2008,32(3):70-74.LIAO Ruijin,WANG Qian,LUO Sijia,et al.Condition assessment model for power transformer in service based on fuzzy synthetic evaluation[J].Automation of Electric Power Systems,2008,32(3):70-74.
[9] 郑蕊蕊,赵继印,赵婷婷,等.基于遗传支持向量机和灰色人工免疫算法的电力变压器故障诊断[J].中国电机工程学报,2011,31(7):56-63.ZHENG Ruirui,ZHAO Jiyin,ZHAO Tingting,et al.Power transformer fault diagnosis based on genetic support vector machine and gray artificial immune algorithm[J].Proceedings of the CSEE,2011,31(7):56-63(in Chinese).
[10] 郭创新,朱承治,张琳,等.应用多分类多核学习支持向量机的变压器故障诊断方法[J].中国电机工程学报,2010,30(13):128-134.GUO Chuangxin, ZHU Chengzhi, ZHANG Lin,et al.A fault diagnosis method for power transformer based on multiclass multiple-kernel learning support vector machine[J].Proceedings of the CSEE,2010,30(13):128-134.
[11] 董明,严璋,杨莉,等.基于证据推理的电力变压器故障诊断策略[J].中国电机工程学报,2006,26(1):106-114.DONG Ming,YAN Zhang,YANG Li,et al.An evidential reasoning approach to transformer fault diagnosis[J].Proceedings of the CSEE,2006,26(1):106-114.
[12] WANG Z,LI J,SOFIAN D M.Interpretation of transformer FRA responses-Part I:influence of winding structure[J].IEEE Transactions on Power Delivery,2009,24(2):703-710.
[13] SHINTEMIROV A,TANG W H,WU Q H.Transformer winding condition assessment using frequency response analysis and evidential reasoning[J].IET Electric Power Applications,2010,4(3):198-212.
[14] LUDWIKOWSKI K,SIODLA K.Investigation of transformer model winding deformation using sweep frequency response analysis[J].IEEE Transactions on Dielectrics and Electrical Insulation,2012,9(6):1957-1961.
[15] KENNEDY G M,MCGRAIL A J,LAPWORTH J A.Transformer sweep frequency response analysis(SFRA)[J].Energize publishers,2007:28-33.
[16]TRIANTAPHYLLOU E,KOVALERCHUK B,MANN L,et al.Determining the most important criteria in maintenance decision making[J].Journal of Quality in Maintenance Engineering,1997,3(1):16-28.
[17] YANG J B,XU D L.On the evidential reasoning algorithm for multiple attribute decision analysis under uncertainty[J].IEEE Transactions on Systems,Man and Cybernetics,Part A:Systems and Humans,2002,32(3):289-304.
[18] TANG W H,SPURGEON K,WU Q H,et al.An evidential reasoning approach to transformer condition assessments[J].IEEE Transactions on Power Delivery,2004,19(4):1696-1703.
[19] YE F,LI Y N.Group multi-attribute decision model to partner selection in the formation of virtual enterprise under incomplete information[J].Expert Systems with Applications,2009,36(5):9350-9357.
[20] WU W Y,LIN C,KUNG J Y,et al.A new fuzzy TOPSIS for fuzzy MADM problems under group decisions[J].Journal of Intelligent and Fuzzy Systems,2007,18(2):109-115.
[21] JOUSSELME A L,GRENIER D,BOSSÉ É.A new distance between two bodies of evidence[J].Information Fusion,2001,2(2):91-101.
[22] HUANG S F,CHENG C H.GMADM-based attributes selection method in developing prediction model[J].Quality&Quantity,2013,47(6):3335-3347.

