基于数据驱动的风机组网系统故障诊断∗
赵新龙 吴鹏飞 徐建锋
(1.浙江理工大学机械与自动控制学院;2.浙江上风高科专风实业有限公司)
基于数据驱动的风机组网系统故障诊断∗
赵新龙1吴鹏飞1徐建锋2
(1.浙江理工大学机械与自动控制学院;2.浙江上风高科专风实业有限公司)
风机组网系统的大型化、复杂化、综合化特性增加了其故障诊断的难度。基于主元分析、Kullback-Leibler散度、多分辨率奇异值分解的数据驱动方法,通过故障检测、故障定位、故障分析三个步骤,实现了对风机组网系统中增益性故障以及周期性冲击故障的诊断与分析。利用主元分析与Kullback-Leibler散度结合,实现系统故障检测;利用Z分解和Kullback-Leibler散度来故障定位,将故障定位到具体的风机;利用多分辨率奇异值分解来分析故障种类。仿真结果证明了该方法的有效性。
风机组网系统;主元分析;Kullback-Leibler散度;多分辨率奇异值分解
0 引言
相对于单台风机而言,风机组网系统具有大型化、复杂化、组网化的特性,增加了故障诊断的难度,需要更加精确的诊断方法。并且在判断系统是否发生故障之后,还需要将故障定位到相应的风机上,增加了风机组网系统故障诊断的难度。
故障诊断技术可以分为基于模型分析方法、定性经验和基于数据驱动的方法[1]。基于分析模型的方法需要有足够的信息和过程精确的定量的数学模型,其实际应用效果并不理想。基于定性经验的方法在分析中需要掌握复杂的专业知识和长期积累经验的工程人员。基于数据驱动的故障诊断方法包括基于统计分析的方法、基于信号分析的方法以及基于定量知识的数据分析方法,具有诊断精度高、对系统要求低、对工程人员经验要求低等优点逐渐成为了故障诊断的主要方法。
主元分析(PCA)是一种应用广泛的降维方法,在故障诊断、数据压缩和模式识别等领域都发挥着重要的作用[2-3],对数据协方差矩阵选取一定维数的特征向量,与原始矩阵相乘得到降维后的数据。KL散度(Kullback-Leibler Divergence)又称相对熵,是一种基于统计分析的故障诊断方法,它可以比较两个分布的不同程度,应用于模式识别[4]、异常探测[5]、故障诊断[6]等领域。KL散度可以较精确地检测出系统中存在的故障,更加直观地以数值的形式表现出来,但难以判断故障的类型。多分辨率奇异值分解(MRSVD)是一种基于信号分析的故障诊断方法,通过多次奇异值分解将原始信号分解到一系列不同层次空间,得到具有不同分辨率的近似信号和细节信号的多分辨率分解[7],再通过对近似和细节信号进行分析,来判断故障是否发生。MRSVD可以无相移的对信号进行降噪,提取出系统中存在的周期性故障,但检测故障精度不高。
本文融合了PCA、KL散度和MRSVD三种数据驱动方法完成对风机组网系统的故障诊断,利用PCA与KL散度结合的方法完成了对系统是否发生故障的判断;利用Z分解和KL散度完成了对故障的定位,利用MRSVD完成了故障的判断并简单分析了故障。在故障诊断过程中,以风机轴承的振动信号作为分析对象[8-9]。模拟实验证明,基于该方法可以检测出风机组网系统中出现的增益性故障和周期性冲击故障,并对故障进行具体定位以及识别故障种类。
1 结合PCA与KL散度的故障检测
对风机轴承中常见的增益性故障和周期性冲击故障进行诊断。增益性故障多发生于故障早期[10],表现为在短时时间窗内,信号的幅值有数值为a的额外增益。假设信号 x=(x1,…,xb,…,xc,…,xN)在间隔[b,c]之间发生了增益性故障,设故障的额外增益为a,则信号区间[b,c]的幅值为:

令G=1+a,则:

周期性冲击故障是当轴承表面的某一原件表面存在故障时、轴承存在点蚀或局部脱落时,在其振动信号中会有周期性的冲击存在[11]。长时间的冲击会加剧冲击的幅度,影响轴承的寿命,严重时会造成灾难性事故。
利用风机轴承的振动信号对风机组网的故障诊断主要分为3步:
第1步,故障检测:运用PCA与KL散度结合的方法判断风机组网系统中是否有风机存在故障。
第2步,故障定位:运用了Z分解与KL散度的方法来判断风机组网系统中哪部风机存在故障。
第3步,故障分析:运用MRSVD的方法判断风机发生的故障类型,并对故障进行初步的特性分析。
通过PCA与KL散度结合的方法进行整体故障的检测,首先将各个风机进行编号,进而确定所要分析数据的格式,将数据的列数与风机的数目相等,数据的行数与采样点数相等;再对各风机的健康运行时轴承的振动信号进行采样,得到参考数据。相应的,风机待检测状态时,对各风机运行时轴承的振动信号进行采样,得到待检测数据。将得到的参考数据与待检测数据分别进行主元分析,得到各自的第一得分向量,再对得分向量进行概率密度估计,通过KL散度公式,求出其KL散度值来判断是否发生故障。其检测过程如图1所示。

图1故障检测过程图Fig.1 The fault diagnosis process chart
在概率密度的估计上,对于未知的概率分布,利用核密度估计来估计概率密度函数,通过采样,得到选取点的离散概率密度值,再来求取KL散度值;对于已知的概率分布,可以通过距估计来估计相应的参数,得到概率密度函数,来求得相应的KL散度值。例如风机轴承常见的正态分布,假设经过距估计得到参考信号的概率密度函数 f(x)和待检测信号的概率密度函数g(x)分别服从均值和方差为的正态分布,则:

Kullback和Leibler将 f(x)和g(x)的KL信息定义为[15]:

在KL信息的基础上,KL散度定义为:

将 f(x)和 g(x)依次代入公式(5),再代入公式(6),得到KL散度公式为:

对于门槛值εsafe的选取,需要依据噪声的水平,信噪比的大小来选取[16]。
2 结合Z分解与KL散度的故障定位
在确定风机组网系统中发生了故障之后,需要判断是哪台风机发生了故障。本文通过对风机组网系统数据进行Z分解,从而以少量的工作来完成对故障的定位。
假设风机的台数为n台,且每次故障只发生一种,为增益性故障或周期性冲击故障,通过Z分解[17],可以将n维数据分解成Kz维数据(Kz<n),其中Kz为:

假设分解后的维数为m,即:

将n台风机编号为x1到xn,Z分解后的向量为z1到zm,于是得到相应的矩阵为:

其中2m-a+1+2m-a<n。
由于n台风机的n维数列到m维向量实质是通过二进制编码的方式。在检测发生故障的风机时,先检测z1到zm这m个分解向量,求出各个分量相对于参考分量概率分布的差异程度,即KL散度,再分析他们的组合方式来判断是哪台风机发生了故障。经过Z分解,只需检测m个信号,而不需要对每台风机的信号进行检测,就可以判断具体是哪台风机发生了故障,减少了工作量。
3 基于MRSVD分解的故障分析
经过对风机组网系统的故障定位后,可明确故障发生位置,进而对发生故障的风机振动信号进行分析,判断出相应的故障种类。对于增益性故障,可以初步判断其故障严重程度,对于周期性冲击故障,可以近似判断其冲击的频率。
将出现故障的风机轴承信号进行数次MRSVD分解,得到相应的近似信号和细节信号,通过对近似信号和细节信号的观察与分析,判断出故障种类。对于增益性故障,可以在细节信号中直观看到出现增益性故障的区间,并估计增益的幅值,判断故障的严重程度。对于周期性冲击故障,可以在细节信号中求出冲击的间隔,进而计算出冲击信号出现的频率。
4 仿真和结果分析
现以一个由7台风机组成的风机组网系统来讨论,假设它们的轴承振动信号服从正态分布,对其采样2 000个点,对他们编号为x1到x7,其分布如下所示:

对于增益性故障,将x1的[1 500:2 000]区间增加150%的增益;而对于周期性冲击故障,在x1上以每隔200点的频率叠加一个近似于正弦信号的微弱冲击信号。为了模拟噪声环境,对信号叠加信噪比为30dB的噪声。第1步,对风机组网系统的故障检测。将两组含有故障信号的数据与无故障的参考信号组成的数据进行主元分析,设定主元向量数目为4,选取各自的第一主元,三组第一主元的概率分布图如图2所示。
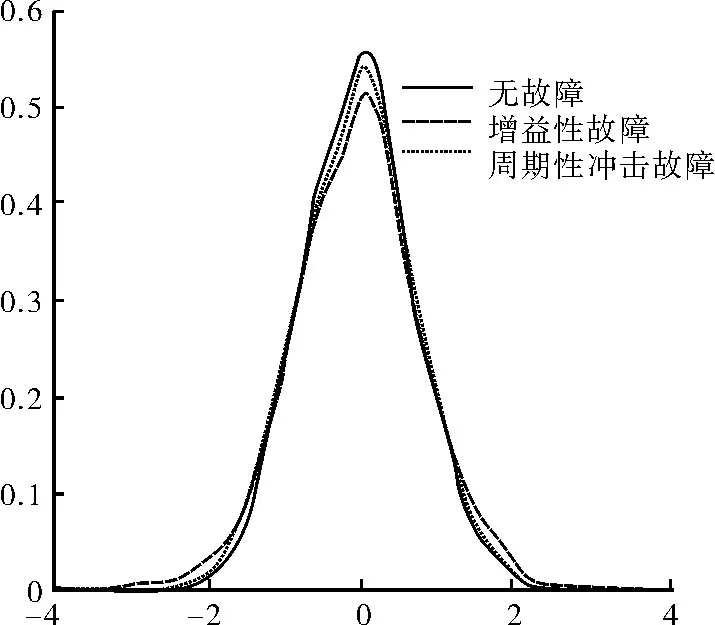
图2 三种状态下的第一得分向量的概率分布图Fig.2 The probability distribution of the first vector quantity in three conditions
由于PCA得到的主元向量是原始数据向量的线性组合,而原始各向量均满足正态分布,因此得到的得分向量也满足正态分布。得知主元向量的分布后,通过一阶和二阶距估计,求得分布的参数,进而得到概率密度函数。仿真中,分别对增益性故障和周期性冲击故障仿真了50次,在这50次中,其中第12次到15次,25次到26次,40次到45次,共12次是存在故障的,而其余的次数是不存在故障的。图3是增益性故障的仿真结果,图4是周期性冲击故障的仿真结果,从图中可以看出,对于故障的判定,通过KL散度值可以精确的判定出是否存在故障。

图3 增益性故障仿真Fig.3 The simulation of gain fault
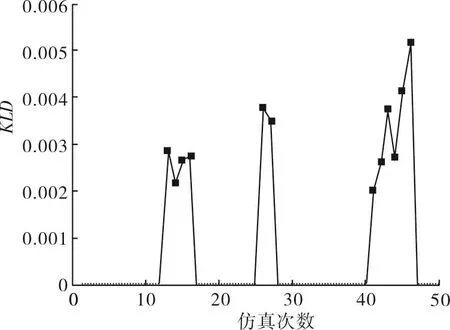
图4 周期性冲击故障仿真Fig.4 The simulation of periodic fault
对增益性故障而言,其增益的幅值也会影响其KL散度值。图5展示了对于不同增益下故障的KL散度值变化情况。在仿真实现的50次中,第5次到第9次,增益为110%,之后每当尾数为5到9的仿真的故障增益依次递增10%,如第45次到第49次的增益为150%。从图中可以看出故障增益与KL散度值成正相关关系。因此可以从KL散度值可以看出故障的严重程度。
后来她自己开发出了多种蛋糕,在色彩、配料、种类等种种过程中都融入了特色的东西;而这些特色和灵感恰恰来源于她之前对美学的学习,来源于她的画画、摄影、设计的经验。

图5 故障增益幅值与KL散度值的关系Fig.5 The relationship between fault gain amplitude andKLD
在风机组网系统的故障的定位中,由于存在7组风机,通过Z分解,得到Kz=3,根据Z分解得到,3组分量如下所示:

其故障位置与分解后的分量的逻辑关系如表1所示。

表1 故障定位与分量逻辑关系Tab.1 The logical relationship between fault location and component vector
Z分解是通过系数为二进制的x1到x7的向量的线性组合,因此得到的分解向量也满足正态分布。仿真中,对增益性故障和周期性冲击故障进行40次仿真,其中前20次为无故障时的KL散度值,后20次是x1有故障时的KL散度值。其中KL散度值是将待检测的z1到z3分量与相对应的参考分量求取KL散度得出的。增益性故障的z1到z3分量的KL散度值变化如图6所示,而周期性冲击故障相应的KL散度值变化如图7所示,分别对应z1,z2和z3的KL散度值。
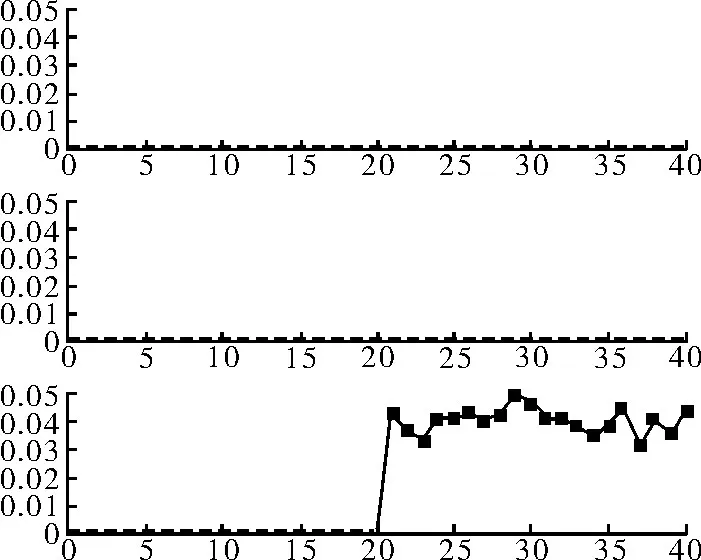
图6 增益性故障z1到z3的KL散度值Fig.6 TheKLDof gain fault fromz1toz3

图7 周期性冲击故障z1到z3的KL散度值Fig.7 TheKLDof periodic impact fault fromz1toz3
通过z1到z3的变化和表2的对应关系,得到了故障的位置为x1,于是继续对x1进行分析,得到参考信号和两种故障信号的时域图,如图8~图10所示。
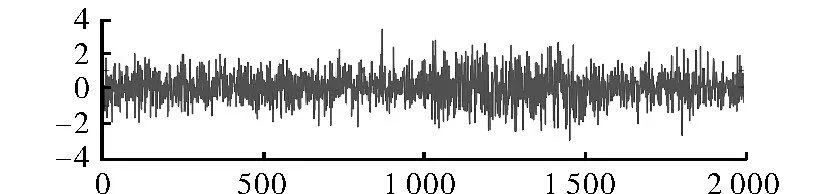
图9 x1发生增益性故障时域图Fig.9 Thex1time domain figure of gain fault

图10 x1发生周期性冲击故障时域图Fig.10 Thex1time domain figure of periodic impact fault
从上图中很难看出故障种类,对两组故障信号进行MRSVD分析,分别得到了各自的近似信号和细节信号,通过对近似信号和细节信号的分析来判断故障的种类,图11到图14是两组故障信号分别进行了8次MRSVD得到的近似信号和细节信号的时域图。

图11 x1发生增益性故障的近似信号时域图Fig.11 Thex1approximate signal time domain figure with gain fault

图12 x1发生增益性故障的细节信号时域图Fig.12 Thex1detail signal time domain figure with gain fault

图13 x1发生周期性冲击故障的近似信号时域图Fig.13 Thex1approximate signal time domain figure with periodic impact fault
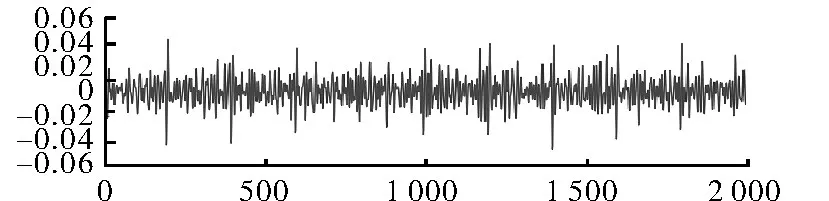
图14 x1发生周期性冲击故障的细节信号时域图Fig.14 Thex1detail signal time domain figure with periodic impact fault
从图12和图14中可以明确的看出故障的种类。在图12中,可以看到信号在1 000~1 450采样点之间的幅值明显大于其他采样点的幅值;而从图14中也可以明显的看到存在周期性冲击故障,每隔大约200个点会存在一次冲击。
对于增益性故障,可以通过故障检测得到KL散度值,再与图6中的数据进行对比,估计故障增益的幅值,进而判断故障的严重程度。
对于周期性冲击故障,可以对周期性信号的频率进行估计。假设对风机轴承2 000个采样点的采样时间为0.1s,则故障发生的间隔为0.01s,周期性冲击频率为100Hz。
5 结论
1)本文利用了数据驱动的方法完成了对风机组网系统的故障诊断。通过对系统进行故障检测、故障定位与故障分析,对系统中发生的增益性故障和周期性冲击故障实现诊断。
2)在诊断过程中采用了PCA模型、KL散度方法和MRSVD方法,通过PCA与KL散度结合来检测故障;通过Z分解与KL散度方法来定位故障;通过MRSVD来分析故障。在故障定位中应用了Z分解的方式,减少了分析的工作量,使得故障的定位更加直观,明确。
3)KL散度在故障检测中精度高,但难以判断故障种类,而MRSVD可以直观的在信号时域图中分辨故障种类,两者结合使用,提高准确度。
[1]李晗,萧德云.基于数据驱动的故障诊断方法综述[J].控制与决策,2011(1):1-9,16.
[2]JV.Kresta,JF.Macgregor,TE.Marlin.Multivariate Statistical Monitoring of Process Operating Performance[J].The Canadian Journal of Chemical Engineering,1991,69(1):35-47.
[3]陆宁云,王福利,高福荣,等.间歇过程的统计建模与在线监测[J].自动化学报,2006,32(3):400-410.
[4]J.Silva,S.Narayanan.Average divergence distance as a statistical discrimination measure forhidden Markov models[J].IEEE Transactions on Audio,Speech,and Language Processing,2006,14(May(3)):890-906.
[5]M.Afgani,S.Sinanovic,H.Haas.Anomaly detection using the Kullback- Leibler divergence metric. in:1st International Symposium on Applied Science on Biomedical and Computer Technology,2008:1-5.
[6]J.Harmouche,C.Delpha,D.Diallo.Faults diagnosis and detection using principal component analysis and Kullback-Leibler[J].IECON 2012-38th Annual Conference of the IEEE Industrial Electronics Society,2012,2(1):3907-3912.
[7]赵学智,叶邦彦,陈统坚.多分辨奇异值分解理论及其在信号处理和故障诊断中的应用[J].机械工程学报,2010(20):64-75.
[8]王英丰.风机的扭转振动及实例分析[J].风机技术,2017(2A):54-58.
[9]杨梦迪,施康.某高转速地铁风机强度、振动数值分析和优化设计[J].风机技术,2016(6):40-44,66.
[10]R.Isermann.Fault-Diagnosis Systems:An Introduction from Fault Detection to Fault Tolerance[M].Springer,Berlin,Heidelberg,2006.
[11]邵毅敏,周晓君,欧家福,等.增强型滤波及冲击性机械故障特征的提取[J].机械工程学报,2009,45(4):166-171.
[12]王颖.基于振动信号地铁轴流风机的故障诊断分析[J].风机技术,2017(2A):49-53.
[13]何小锋,何利鹏.排粉风机的振动分析及处理[J].风机技术,2016(2):94-96.
[14]James M.Sorokes,D.Fred Marshall,Mark J.Kuzdzal.关于作用在离心压缩机上的流体激振力以及由此产生的转子振动特性综述[J].风机技术,2017(1):43-64.
[15]S.Kullback,R.A.Leibler.On information and sufficiency[J].The Annals of Mathematical Statistics,1951,22(1):79-86.
[16]Jinane Harmouche,Claude Delpha,Demba Diallo.Incipient fault detection and diagnosis based on Kullback-Leibler divergence using Principal Component Analysis:PartI[J].Signal Processing.,2014(94):278-287.
[17]C.Delpha,D.Diallo,A.Youssef.Kullback-Leibler Divergence for fault estimation and isolation:Application to Gamma distributed data[J].Mechanical Systems and Signal Processing,2017(93):118-135.
Data Driven Fault Diagnosis of a Fan Network System
Xin-long Zhao1Peng-fei Wu1Jian-feng Xu2
(1.College of Mechanical Engineering and Automation;2.Zhejiang Shang Feng Special Blower Industrial Co.,Ltd.)
The fault diagnosis of large-scale,complex and integrated fan network systems is performed by three data driven methods based on principal component analysis,Kullback-Leibler divergence and multi-resolution singular value decomposition.Fault detection,fault location and fault analysis has been realized in three steps,i.e.,gain fault,periodic impact fault diagnosis and analysis of fan network system.The fault detection system uses the combination of principal component analysis and Kullback-Leibler divergence,the fault location,i.e.,the fault of a specific fan is determined using Z-decomposition and Kullback-Leibler divergence,and multi-resolution singular value decomposition analyses the fault type.The simulation results prove the effectiveness of these methods.
fan network system,principal component analysis,Kullback-Leibler divergence,multi-resolution singular value decomposition
浙江省重点科技创新团队项目(2013TD18)
2017-10-14 浙江 杭州 310018
TH43;TK05
1006-8155-(2017)06-0075-06
A
10.16492/j.fjjs.2017.06.0013

