正交异性材料双层板弯曲断裂分析
韩贵花,张雪霞,赵文彬,王 慧
(太原科技大学 应用科学学院,太原 030024)
正交异性材料双层板弯曲断裂分析
韩贵花,张雪霞,赵文彬,王 慧
(太原科技大学 应用科学学院,太原 030024)
研究含界面裂纹正交异性复合材料双层板在弯曲载荷作用下的裂纹尖端场问题。利用复变函数方法,引入含待定实系数的挠度函数,利用待定系数法,建立满足边界条件的非齐次线性方程组。求解得到满足控制方程和边界条件的挠度函数,推导出特征方程判别式均大于零时受弯曲载荷作用的正交异性复合材料双层板界面裂纹尖端的应力、应力强度因子、弯矩和扭矩的解析表达式。最后通过算例分析了极角取定值时,弯矩随极径改变的变化曲线以及极径取定值时,弯矩的角分布曲线。
正交异性材料双层板;界面裂纹;复变函数;弯矩
复合式材料双层板是由两种或者两种以上不同性能的材料构成,粘结部分存在界面,由于材料的制作与设计,界面处通常会有缺陷。在载荷的影响下,裂纹处经常出现应力集中现象,以致于裂纹扩展,最终导致材料结构失效。目前,很多研究者对复合材料双层板界面断裂力学进行了研究。A. D. Szekrenyes[1]利用三阶剪切变形板式理论分析了复合型材料式双层板在裂纹缺陷附近的应力以及能量释放率,考虑到平衡性问题再加上位移在界面处应具有连续性,制定出满足边界条件的控制方程。并用J积分方程对II、III型裂纹在缺陷尖端处的能量型释放率的分布形式进行了一定分析。SihGc[2]等对各向同性式双层材料板在纯弯载荷影响下的界面缺陷问题进行了分析,推理出含界面裂纹复合式材料在裂尖附近全场解的理论公式。郑百林[3]等通过傅里叶级数展开方法将位移场的位移函数用级数形式来代替,通过傅里叶变换,对复合式材料双层板的Ⅲ型界面裂纹尖端的应力场进行分析,并指出裂纹尖端存在奇异性,得到了全场解。杨维阳[4-6]等对复合式材料单层板裂纹在不同载荷情况的裂纹尖端场都进行了理论研究及力学分析,推算出受不同载荷作用下的复合材料板在裂尖处的应力场和位移场。张雪霞[7-8],李俊林[9]等对正交异性式双层材料板关于Ⅱ型和弯曲界面裂纹尖端附近的力学性态分别进行了理论探讨,凭借构造新的含待定系数的应力函数,根据复变法,推算出了含Ⅱ型界面裂纹的复合式材料双层板在裂纹尖端处受面内载荷作用下的应力、位移的理论计算公式,并对振荡奇异性进行了说明。Xian-Fang Li, GuoJin[10]对双材料在剪切力加载到环形界面裂纹表面时的应力强度因子以及尖端场问题进行了分析。根据裂纹的轴对称问题得到了混合边界条件,求解出一组没有振荡奇性的封闭解。M. Li[11], T. H. Long Rong[12]等用有限元法分别在笛卡儿坐标和极坐标下分析了界面裂纹的应力强度因子和应力场。基于拉格朗日插值法直接构造一阶偏微分方程矩阵,从而获得一组线性代数方程形式的控制方程和边界条件。用边界配置法对裂纹尖端奇异性和应力场进行了讨论和的数值求解,推导出复合式材料双层板在裂尖附近全场解的表达式。

1 力学模型
含有中心穿透裂纹长为2a的正交异性复合材料双层板,厚度为h,x轴和y轴与弹性主方向的关系为平行,受对称弯曲载荷M0作用,如图1所示,在直角坐标系xoy下,设y>0部分为正交异性双材料复合材料板1,y<0部分为正交异性复合材料板2,y=0,x
每种复合式材料的柔度系数(A11)j, (A12)j, (A22)j, (A66)j刚度系数(D11)j, (D22)j, (D12)j和抗扭刚度系数(D66)j与它的弹性常数Ej1,Ej2,νj1,νj2,μj之间满足关系如下:

(1)
根据弹性板的弯曲理论可知,挠度函数wj所满足的控制方程为[4]:

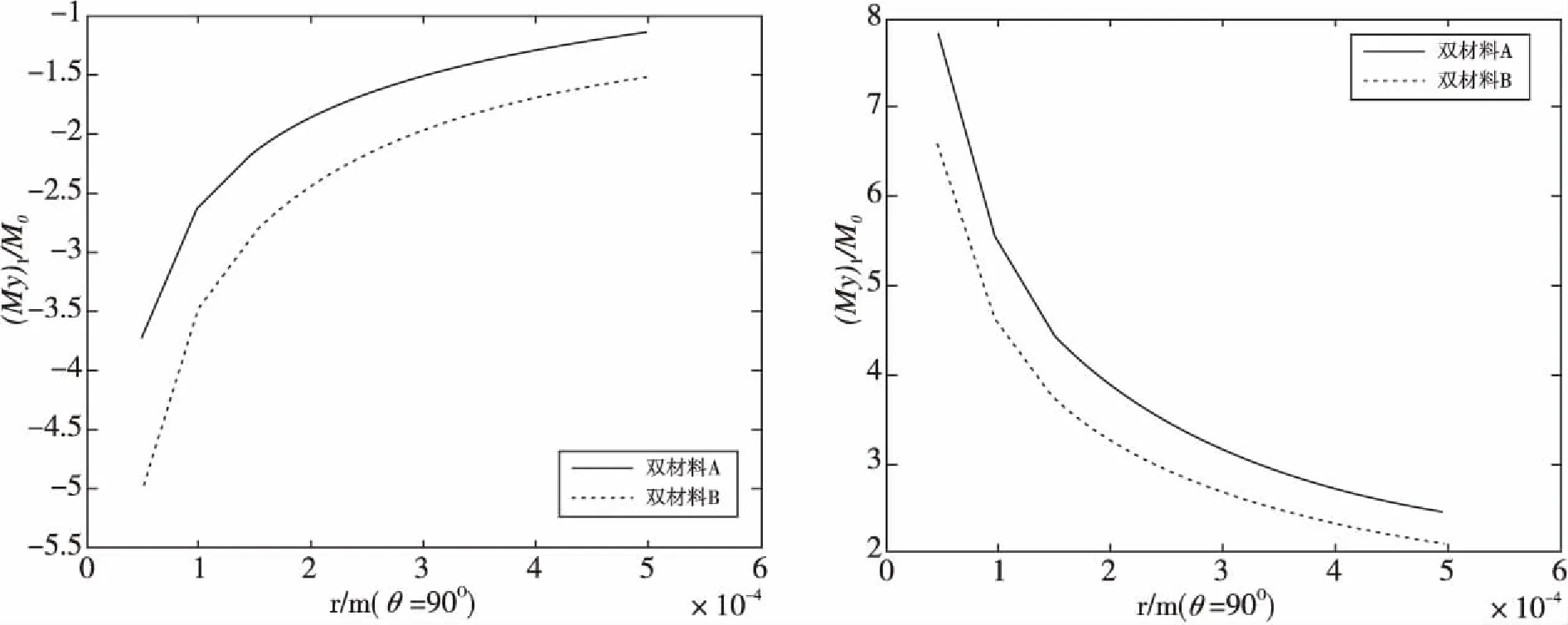
图1 含界面裂纹正交异性双层材料板
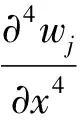
(2)
受弯曲载荷作用的正交异性纤维增强复合材料双层板界面裂纹边界条件为:
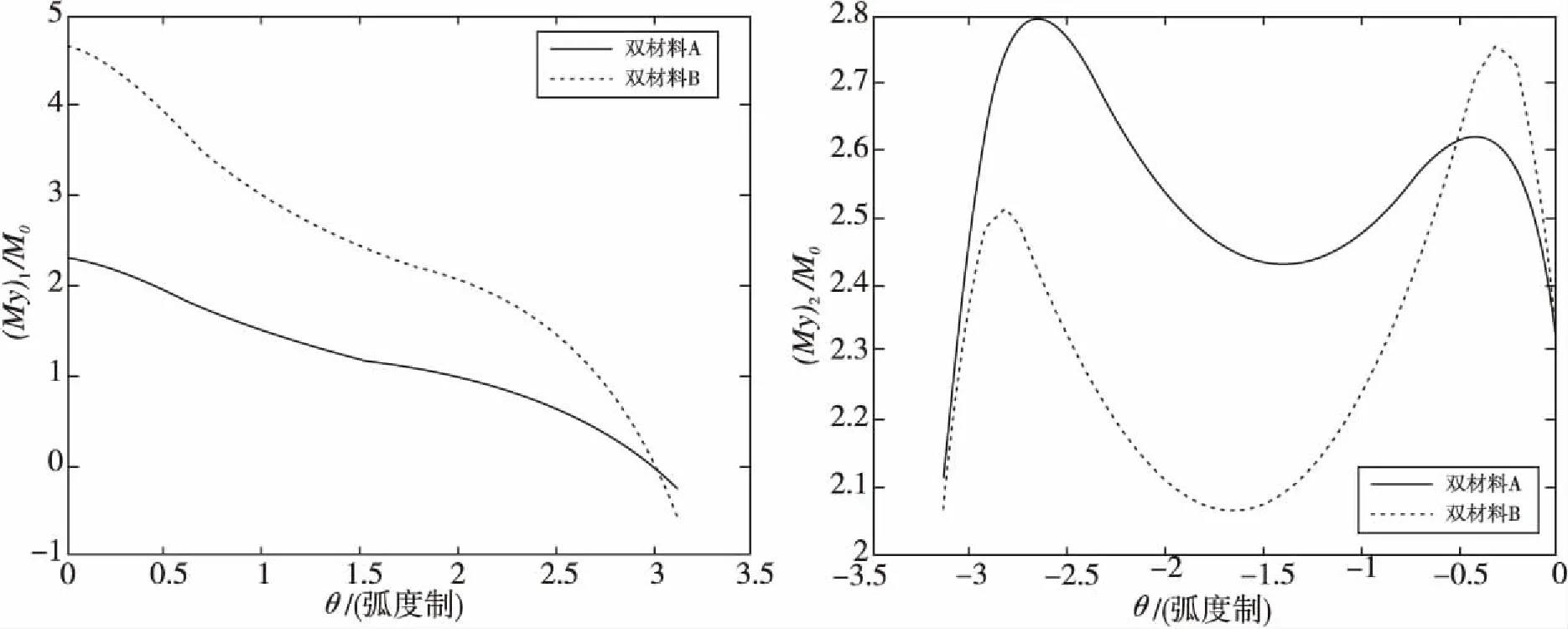
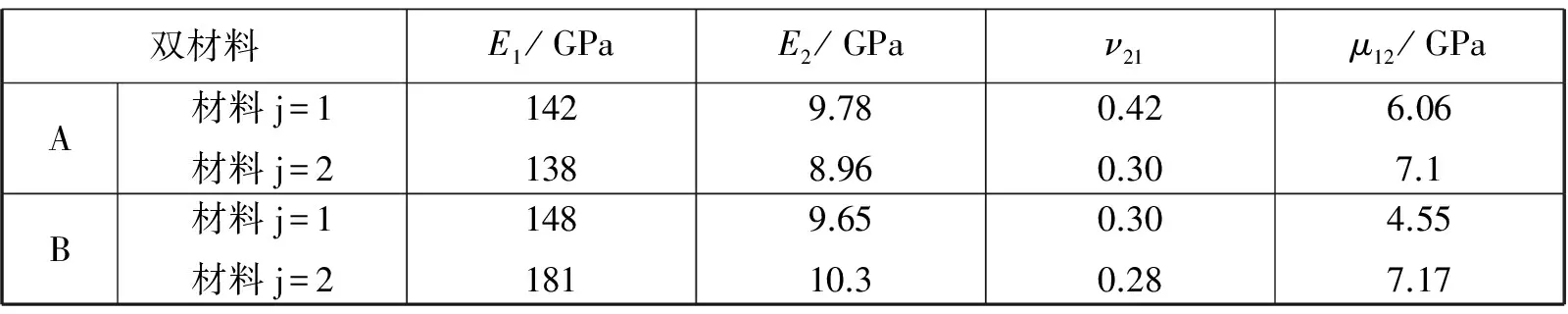
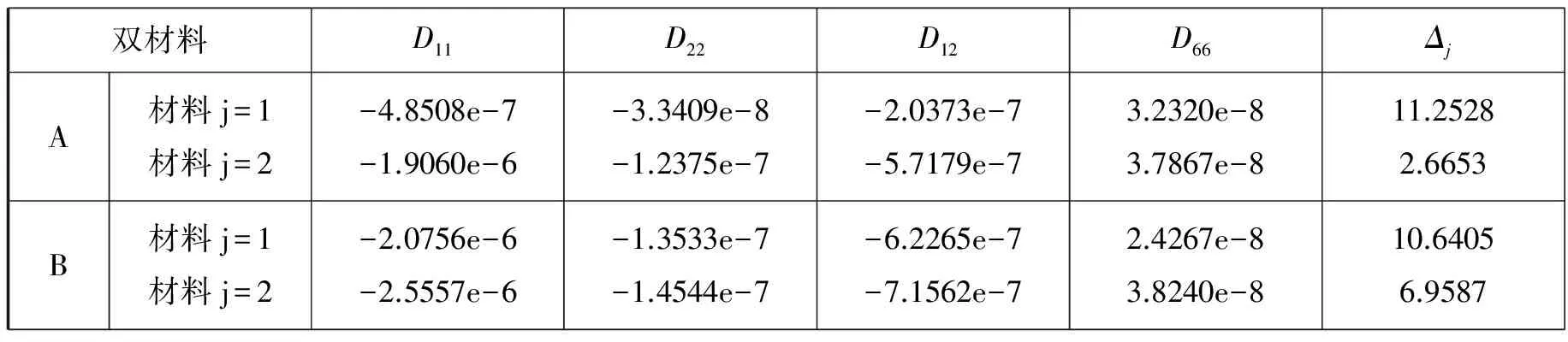
y=0,x (3) y=0,x>a:(My)1=(My)2,(Ny)1=(Ny)2 (4) y→+:(My)j=M0,(Hxy)j=0 (5) 于是讨论受弯曲载荷作用下的正交异性复合式双材料界面裂纹断裂问题就转化为非齐次偏微分方程组式(3)-式(5)的边值问题。下面利用复变函数方法,通过引入含参数的挠度函数,从而求解偏微分方程组边值问题。 令中面挠度函数wj=wj(x+sjy)可得控制方程(2)的特征方程为: (D22)jsj4+2[(D12)j+2(D66)j]sj2+(D11)j=0 (6) 这是双二次方程,定义其判别式: (7) 本文讨论两种材料的判别式Δj均大于零,即Δ1>0,Δ2>0的情形。 所以特征方程式的根为:sjk=iβjk,sj(k+2)=-iβjk, (j,k=1,2) (8) 式中βj2>βj1>0, 由(6)式可知: (9) 若记:zjk=x+sjky=xjk+iyjk (10) 利用复变函数和微积分知识可知: (11) 根据(11)式,那么方程(2)式就可化为广义形式的重调和方程: (12) (13) (14) 由方程式(14)和复数表示式(10)可知,复变量zjk的解析函数的实部或虚部都是基本方程(2)式的解,即方程一定有解析解。 考虑到k,m=1,2,故选取挠度函数wj为如下含有两个应力奇异指数λ1,λ2的级数形式: (15) 根据弹性板弯曲理论的应力、弯矩和扭矩的基本公式,可以得到: iBjk,λm)sjk2wjk,λm(zjk)] (16) iBjk,λm)sjk2wjk,λm(zjk)] (17) (18) iBjk,λm)sjk2wjk,λm(zjk)] (19) iBjk,λm)sjk2wjk,λm(zjk)] (20) (21) [(Ajk,λm-iBjk,λm)sjk3wjk,λm′(r,θ)] (22) 考虑到复合材料双层板受远场弯曲载荷M0的作用,特别选取挠度函数为: (23) (24) 因为zjk=x+sjky,zjk-a=rcosθ+sjkrsinθ, 所以zjk=rcosθ+sjkrsinθ+a, 从而: 将式(24)代入式(20)、式(22),再结合直角坐标与极坐标之间的变换关系,再带进边界条件式(3),可得: [(D22)1β112-(D12)1]cosλmπ·A11,λm+[(D22)1β122-(D12)1]cosλmπ·A12,λm +[(D22)1β112-(D12)1]sinλmπ·B11,λm+[(D22)1β122-(D12)1]sinλmπ·B12,λm=0 (25) {β11[(D12)1+2(D66)1]-(D22)1β113}sinλmπ·A11,λm-{β11[(D12)1+2(D66)1]- (D22)1β113}·cosλmπ·B11,λm+{β12[(D12)1+2(D66)1]-(D22)1β123}sinλmπ·A12,λm- {β12[(D12)1+2(D66)1]-(D22)1β123}cosλmπ·B12,λm=0 (26) [(D12)2-(D22)2β212]cosλmπ·A21,λm+[(D12)2-(D22)2β222]cosλmπ·A22,λm-[(D12)2- (27) β21sinλmπ·A21,λm+β22sinλmπ·A22,λm+β21cosλmπ·B21,λm+β22cosλmπ·B22,λm=0 (28) 将式(24)代入式(20)、式(22),再结合直角坐标与极坐标之间的变换关系,再带进边界条件式(4),可得: [(D22)1β112-(D12)1]A11,λm+[(D22)1β122-(D12)1]A12,λm-[(D22)2β212-(D12)2]A21,λm- [(D22)2β222-(D12)2]A22,λm=0 (29) {β113(D22)1-β11[(D12)1+2(D66)1]}B11,λm+{β123(D22)1-β12[(D12)1+2(D66)1]}B12,λm- {β213(D22)2-β21[(D12)2+2(D66)2]}B21,λm-{β223(D22)2-β22[(D12)2+2(D66)2]}B22,λm=0 (30) 将式(24)代入式(20)、式(21),再结合直角坐标与极坐标之间的变换关系,再带进边界条件式(5),可得: (31) (32) β11B11,λm+β12B12,λm=0 (33) β21B21,λm+β22B22,λm=0 (34) 为了方便计算,记: p1=β112D221-D121,q1=β122D221-D121,p2=β212D222-D122,q2=β222D222-D122. 所以方程组式(25)-(34)共十个方程八个未知数,将这非齐次线性方程组的系数以及常数项用矩阵表示,根据系数矩阵与增广矩阵的秩相等是非齐次线性方程组有解的充分必要条件,推导出: (35) (36) 考虑到zjk→a时,则挠度函数 定义受弯曲载荷作用的无限大正交异性复合材料双层板Ⅰ型应力强度因子为: (37) 观察式(35)和式(37)知,在弯曲载荷作用下的正交异性复合材料双层板界面裂纹尖端场的应力强度因子,不仅与裂纹的形状有关系,还取决于双材料的弹性常数。 (38) 将两种材料所得系数A11,λm,A12,λm,A21,λm,A22,λm,B11,λm,B12,λm,B21,λm,B22,λm和式(37)代入式(16)-式(21),分别得到正交异性复合材料板1和正交异性复合材料板2在裂纹尖端附近的应力、弯矩和扭矩的解析表达式: (39) (40) (41) (42) (43) (44) (45) (46) (47) (48) (49) (50) 选取两组正交异性复合材料双层板进行测定,分别得到两组双层材料板的弹性系数如表1所示。将每组材料双层板的弹性常数代入(1)式,得到每组双材料相应材料板的抗弯刚度常数和抗扭刚度常数。并将所得刚度系数代入(7)式,得到每组双材料的判别式如表2所示。 表1 两组双材料中每种材料的弹性常数 Tab.1 Elasticity constant of each material in two sets of double-materials 双材料E1/GPaE2/GPaν21μ12/GPaA材料j=1材料j=21421389.788.960.420.306.067.1B材料j=1材料j=21481819.6510.30.300.284.557.17 给定材料板厚度h=4 mm, 裂纹长2a=10 mm, 将每组双材料参数代入弯矩的解析标表达式(47)和(48)式,当极角取定值时,根据直角坐标系与极角坐标系的转换公式,利用Matlab软件绘出Myj/M0与极径的关系曲线,如图2所示。给定M0,随着极径的增加,正交异性复合材料双层板弯矩Myj逐渐减小,即无量纲弯矩随着极径的增加而减小。 给定材料板厚度h=4 mm, 裂纹长度2a=10 mm, 当极径r=0.5 mm时,将每组双材料参数代入弯矩的解析表达式(47)和(48)式,根据直角坐标系与极角坐标系的转换公式,利用Matlab软件,绘出正交异性复合材料双层板弯矩的角分布曲线,如图3所示。随着极角的增大,弯矩Myj有着相同的增减趋势,但是不对称。 表2 两组双材料刚度系数和判别式 Tab.2 Stiffness coefficient and the discriminant in wo sets of double material 双材料D11D22D12D66ΔjA材料j=1材料j=2-4.8508e-7-1.9060e-6-3.3409e-8-1.2375e-7-2.0373e-7-5.7179e-73.2320e-83.7867e-811.25282.6653B材料j=1材料j=2-2.0756e-6-2.5557e-6-1.3533e-7-1.4544e-7-6.2265e-7-7.1562e-72.4267e-83.8240e-810.64056.9587 选用复变函数法和待定系数法,研究了含界面裂纹正交异性复合材料双层板的弯曲断裂问题,推算出正交异性复合式材料双层板在界面裂尖附近的应力、弯矩、扭矩、和应力强度因子的解析表达式。通过算例对两组双材料的弯矩进行了数值分析,结果表明: (1)在极角大小一定的情况下,随着极径的增加,正交异性复合材料双层板弯矩Myj逐渐减小。 (2)在极径大小一定的情况下,随着极角的增加,正交异性复合材料双层板弯矩Myj有着相同的增减趋势,但是不对称。 图2 双材料弯矩曲线 图3 双材料裂纹尖端弯矩的角分布曲线Fig.3 Angular variation curve of bending moment in the crack-tip field bimaterial [1] SERENENESS A D. Stress and fracture analysis in decontaminated orthotropic composite plates using third-order shear deformation theory[J]. Applied Mathematical Modelling, 2014, 38(15-16): 3897-3916. [2] SIH G C, CHEN E P. Cracks in composite materials[M]. Hague: Martinus Nijhoff Publishers, 1981, 268-274. [3] 郑百林,戴瑛. 双材料反平面问题界面端奇异应力场[J]. 应用力学报, 1999, 16(4): 21-26. [4] 杨维阳,李俊林,张雪霞.复合材料断裂复变方法[M]. 北京:科学出版社, 2005. [5] LI J L, ZHANG S Q, YANG W Y. Stress field near interface crack tip of double dissimilar orthotropic composite materials[J]. Applied Mathematics And Mechanics, 2008,29(8): 1045-1052. [6] 杨维阳,张少琴,李俊林. 正交异性双材料Ⅱ型界面裂纹问题研究[J]. 应用数学和力学,2009, 30(5): 547-555. [7] 张雪霞,崔小朝. 正交异性双材料Ⅱ型界面裂纹尖端的应力场[J]. 兰州理工大学学报, 2011, 37(1): 168-171. [8] 张雪霞,崔小朝,杨维阳,等. 纯弯各向异性符合材料板的断裂分析[J].太原科技大学学报, 2010, 31(3):226-229. [9] 李俊林,张珺.纯弯正交异性双材料界面裂纹尖端应力场研究[J].武汉理工大学学报, 2012,34(2): 32-39. [10] LI X F,TANG G J. Stress intensify factors for an external circular crack at the interface of a bi-material in shear-compression[J]. International Journal of Solids and Structures, 2015, (64-65): 221-231. [11] LI M, MENG L X, WEN P H. Finite block method for interface cracks[J]. Engineering Fracture Mechanics. 2016, 156: 25-40. [12] LENGYEL T H, LONG R. Effect of interfacial slippage on the near-tip fields of aninterface crack between a soft elastomer and a rigid substrate[J].Physical and Engineering Sciences, 2014, 2170(470): 1364-1368. BendingFractureAnalysisofOrthotropicMaterialDoublePlates HAN Gui-hua, ZHANG Xue-xia, ZHAO Wen-bin, WANG Hui (School of Applied Sciences, Taiyuan University of Science and Technology, Taiyuan 030024) The crack tip field problems on the interface crack of orthotropic composite material double-layer plates under the bending load were studied.With the help of the complex function method, introducing the deflection function containing undetermined real coefficients, based on the boundary conditions and undetermined coefficients method, a non-homogeneous linear equations were established. The deflection function of satisfying the boundary conditions were got by solving equations. When the characteristic root discriminant were greater than zero, we can deduc the orthotropic composite materials interface crack tip stress field, the stress intensity factor, the analytic expression of bending moment and torque. Finally, through analyzing by an example, the polar angle is fixed bending moment along with the change of pole diameter change curve and the distribution curve of angle of the bending moment fixing polar diameter. orthotropic bi-materials, interface crack, complex function method, bending moment 1673-2057(2018)01-0076-09 2016-07-20 国家自然基金(51574171),太原科技大学研究生科技创新项目(20151037) 韩贵花(1988-),女,硕士研究生,主要研究方向为偏微分方程及其应用。 O157.5 A 10.3969/j.issn.1673-2057.2018.01.0142 弯曲型界面裂纹的挠度函数
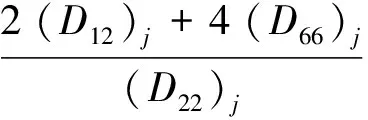
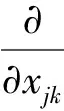
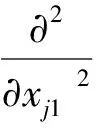

3 待定系数法
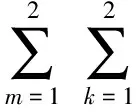
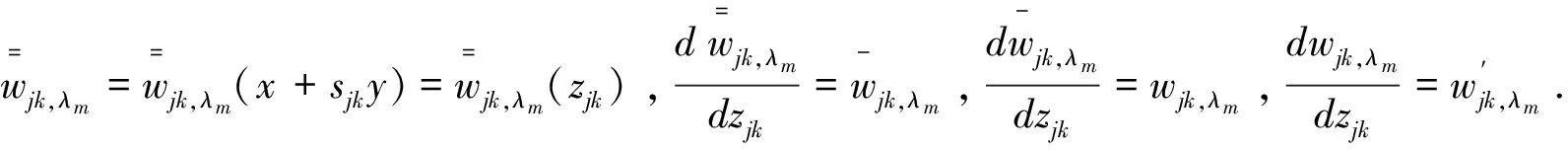









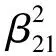


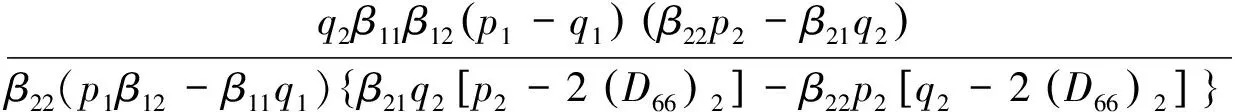
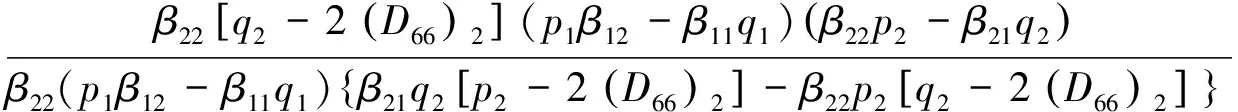
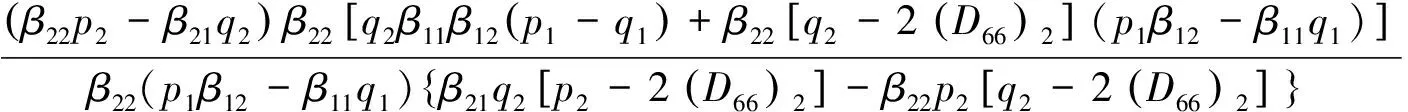
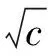

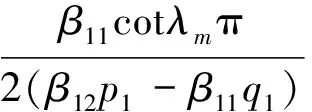
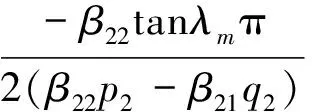
3 应力强度因子
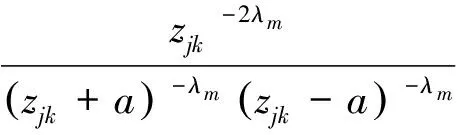
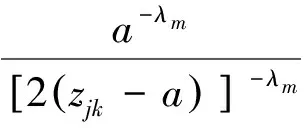
4 应力、弯矩、扭矩表达式
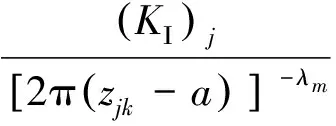
5 算例分析
6 结 论