GPS/BDS网络RTK非组合模型数据处理方法

王兴冰，黄劲松

(武汉大学 测绘学院/地球空间信息协同创新中心，武汉 430079)

GPS/BDS网络RTK非组合模型数据处理方法

王兴冰，黄劲松

(武汉大学 测绘学院/地球空间信息协同创新中心，武汉 430079)

针对网络RTK数据处理方法中组合模型计算复杂及不易扩展的问题，提出一种GPS/BDS网络RTK的非组合模型数据处理方法，并对该方法的定位精度和初始化时间进行分析。在该方法中，多频载波和伪距均参与解算，并将站间单差模糊度、双差电离层和对流层延迟作为待估参数。试验结果表明，BDS双频和三频网络RTK水平定位精度均优于1 cm(1σ外符合)，高程定位精度均优于2 cm(1σ外符合)，单GPS网络RTK定位精度优于单BDS网络RTK定位精度，GPS/BDS双系统网络RTK定位精度优于单GPS和单BDS系统定位精度；不同频率及系统组合的网络RTK能够提供定位服务的平均初始化时间短于30 s。

GPS/BDS；网络RTK；非组合模型；数据处理；定位精度；初始化时间

0 引言

在过去十几年中，网络实时动态差分法(real-time kinematic，RTK)作为一种为用户提供实时高精度导航定位服务的地基增强系统得到了长足的发展，并在测绘领域得到了广泛的应用。随着全球卫星导航系统(global navigation satellite system，GNSS)的日趋完善，网络RTK也向多频率多系统发展。

目前，针对网络RTK的数据处理方法国内外已经有许多学者进行了大量研究，并取得了很多成果。文献[1]针对网络RTK中北斗卫星导航系统(BeiDou navigation satellite system，BDS)三频模糊度固定问题，根据不同的组合系数将BDS三频观测值组合成超宽巷或宽巷观测值，实现了BDS三频观测值模糊度单历元固定，固定成功率达到99.9 %。文献[2]采用将双差载波相位观测值和码伪距观测值组成MW(Melbourne-Wubbena)组合的方法，求得L1、L2的模糊度固定解，经过试验证明可以提供厘米级的定位服务。文献[3]提出了一种利用组合观测值求得的双差模糊度之间的线性关系解决长距离网络RTK双差宽巷模糊度的单历元固定方法。文献[4]中的网络RTK系统采用双差载波相位观测值和双差码伪距观测值组合的方式，采用分步法处理得到L1、L2模糊度值。对于双频组合，现在通行的方法是采用无电离层组合的方式进行处理[5]；但是三频观测值的组合会出现最优组合系数的选择问题[6-7]，组成的观测值不仅要保证模糊的整数特性，还要有较长的波长，并且要降低电离层和组合噪声的影响[8-9]：因此采用组合的方法进行数据处理，模糊度解算需要分步处理，对于三频甚至以后出现的新频点载波观测值必须要选择最优组合系数，计算过程比较复杂。

现有的网络RTK 数据处理过程通常采用载波相位观测值和码伪距观测值组合的方式处理，分步完成模糊度的估算并用固定后的模糊度解算各项误差值[10]。本文提出一种非组合模型，直接估计每颗卫星的双差电离层、基站对流层湿延迟以及站间单差模糊度，随机模型采用基于单基站历元间差分残差的验前估计。相对于组合模型，本文提出的非组合模型对参数直接估计，无需分步；不用考虑不同观测值之间的最优组合系数选择问题，即便将来出现新的卫星导航系统或新的频段载波相位观测值，也可以使用该模型直接进行处理[11]。

1 非组合观测值处理算法

在非组合方法中，对模糊度、每颗卫星的双差电离层和基站天顶湿延迟直接进行估计，该非组合模型中所有卫星系统的多频载波和码伪距观测值均参与解算，并且每个卫星系统选择一颗相应的参考卫星[12]。

1.1 电离层误差参数化方法

本方法采用直接估计每对卫星的双差倾斜总电子含量，由电离层延迟的基本规律(忽略电离层高阶影响)可知载波相位观测值的电离层延迟为

(1)

式中：ρion为信号传播路径上的电离层延迟量；f为载波相位观测值的的频率；S为信号传播路径上总电子含量。很容易由上式得到双差电离层延迟量与双差倾斜总电子含量之间的关系为

(2)

1.2 对流层误差参数化方法

对于对流层延迟量，一般情形下可以分为湿分量和干分量的和，即

ρtrop=Fw·W+Fh·H。

(3)

式中：ρtrop为信号传播路径上的对流层延迟量；Fw和Fh分别为湿分量和干分量的投影系数；W和H分别为天顶对流层湿分量H和天顶对流层干分量。干分量约占总延迟的90 %，湿分量占总延迟量的10 %；其中干分量在已知气象元素(气温、气压、相对湿度)的情形下，模型计算的准确度可达亚毫米级。因此在单基线解算模式中，可以采用先验模型(Saastamoinen模型或者Hopfield模型)改正干分量，只需要估计基线2个基准站之间的相对湿分量。但是在解算过程中，由于2个基准站间的距离相对较近导致2个站的卫星高度角相近，则会导致设计矩阵中的湿分量投影系数几乎相等，形成了病态方程。针对这种情况，本方法采用2个站的卫星高度角的平均值计算投影函数的系数，然后估计2个站的相对天顶方向湿延迟。这种方法可以较好地避免形成病态法方程，增强方程的稳定性。

假设某条基线2个基准站A和B；同时观测了卫星p和q；则可以得到双差对流层延迟量的准确表达式为

(4)

(5)

1.3 非组合观测函数模型

根据电离层误差和对流层误差参数化方法，若A、B为网络RTK基准站，同时观测p、q2颗卫星，其中q为参考卫星，可得到双差方程为：

(6)

(7)

根据上述函数模型，利用卡尔曼滤波方法估计出的每个历元站间单差模糊度[13]、双差电离层参数和天顶站间单差是延迟参数，利用MLAMBDA[14-15]对模糊度进行固定，利用式(8)即可得到电离层参数和对流层参数的固定解

(8)

利用单差模糊度固定解、电离层误差固定解以及对流层误差固定解，根据用户的概略坐标生成用户处的虚拟观测值，并播发给用户完成定位。

1.4 非组合观测值随机模型

随机模型利用历元间差分残差采用验前估计的方法确定[11]。假设载波观测值没有周跳，则前后历元模糊度相等，从而得到历元间差分观测方程为

(9)

由式(9)可得历元间误差方程为

(10)

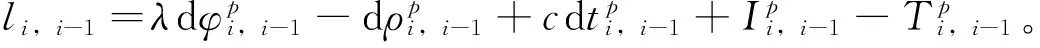
(11)

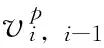
由式(10)可知，对n颗卫星的单频载波观测值联列方程，根据最小二乘原理可得

V=(B(BTD-1B)-1BTD-1-E)L。

(12)

式中：D为协因数矩阵；E为单位矩阵；B为对角线为光速c的n×n对角阵；L为li，i-1组成的n×1矩阵。若观测值真误差为ε，则有

V=(B(BTD-1B)-1BTD-1-E)(BX+ε)=

(B(BTD-1B)-1BTD-1-E)ε。

(13)

将式(13)表示为矩阵形式即

(14)

式中εφi为观测值φi的真误差。每个残差值vi可以表示为

(15)

由式(15)可以看出：各卫星的残差主要取决于该卫星观测值的真误差；其他卫星的真误差则较少反映在该残差中。根据残差进行进一步选权迭代，可以更精确得到各观测值的先验方差[7]。

由于网络RTK基站一般采用高采样率数据，可认为GNSS观测值在较短时间段内符合平稳时间序列特征，因此可以得到

D(εφi)=D(εφi-1)=σ2。

(16)

式中D(εφi)和D(εφi-1)为第i和i-1历元的观测值方差。根据协方差传播律可知，历元间差分观测值的方差

D(εφi.i-1)=D(εφi)+D(εφi-1)。

(17)

根据式(15)可以得到每颗卫星的历元间残差方差可以近似等于观测方差，则有

D(v)=2D(εφi)=2D(εφi-1)=2σ2。

(18)

式中v为当前观测值在时间窗口内的历元间差分残差序列。

对于t时刻的观测值方差，可以采用移动窗口的方法[12]统计其过去一段时间内的方差，以此表征当前时刻观测值精度，因此可以用式(19)计算当前非差观测值的随机模型为

(19)

在实际的数据处理过程中，采用转换矩阵将非差观测值直接变换为双差观测值，其变换矩阵的结构为：

站间单差转换矩阵为

(20)

星间单差转换矩阵为

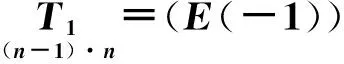
(21)

则双差转换矩阵为

T=T0·T1。

(22)

式中(-1)表示元素全为-1的列向量。根据协方差传播律，通过该双差转换矩阵可以实现由非差观测值方差阵到双差观测值方差阵的变换。

2 实验与结果分析

本文根据自主研发的采用双差非组合函数模型的网络RTK软件，分别对流动站定位精度以及初始化时间做验证分析。

2.1 数据来源

采用2015年年积日第331天采集的采样间隔为1 s的全天数据，包括BASE1、BASE2、BASE3和BASE4 4个基站，具体网形如图1所示。

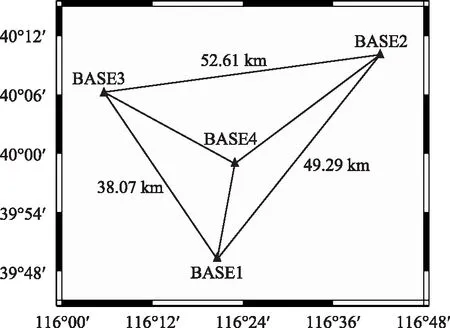
图1 试验基站分布

2.2 流动站定位精度

利用BASE1、BASE2、BASE3等3站作为网络RTK基站，生成BASE4处的虚拟参考站，将BASE4作为流动站，其已知坐标利用长期观测数据通过Gamit解算获得。将用户端确定出的BASE4的坐标与其已知坐标之差对全球定位系统(global positioning system，GPS)/BDS网络RTK中BDS双频、BDS三频、GPS、GPS+BDS双频和GPS+BDS三频5种模式的流动站定位精度进行分析。图2～图6为这5种模式生成的BASE4坐标差在N、E、U方向上的时间序列图。

图2 BDS双频模式N、E、U方向上的坐标差序列

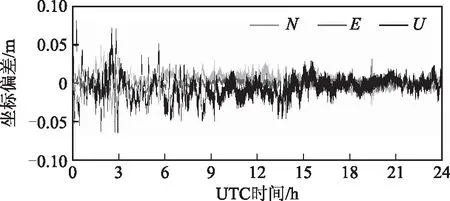
图3 BDS三频模式N、E、U方向上的坐标差序列

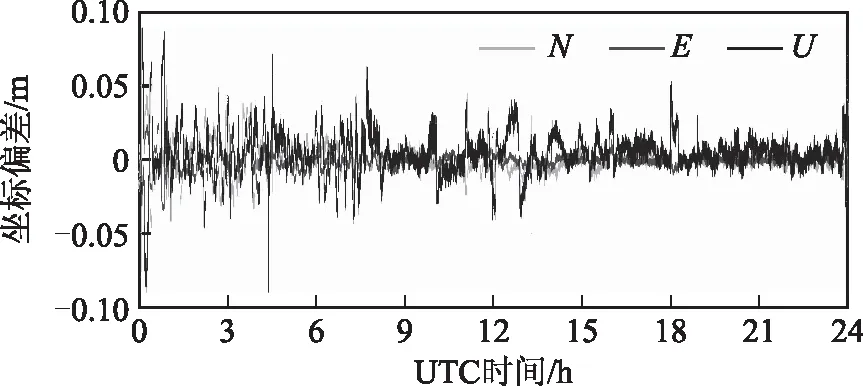
图4 GPS模式N、E、U方向上的坐标差序列

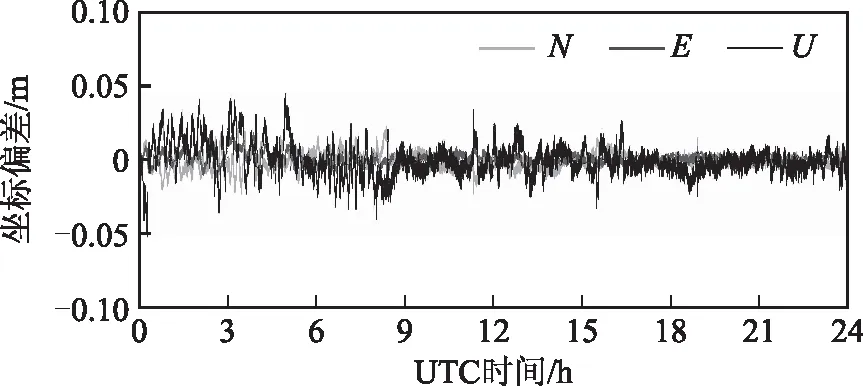
图5 GPS+BDS双频模式N、E、U方向上的坐标差序列

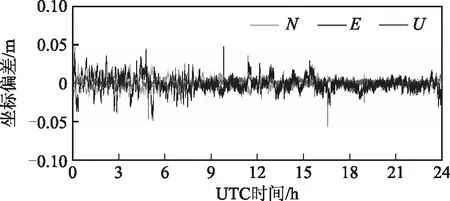
图6 GPS+BDS三频模式N、E、U方向上的坐标差序列

表1为5种定位模式的精度统计，StdN、StdE、StdU表示5种定位模式生成的BASE4的坐标与已知坐标的差值在N、E、U方向上的标准差，固定率是指固定解历元个数占所有解算历元个数的比例。

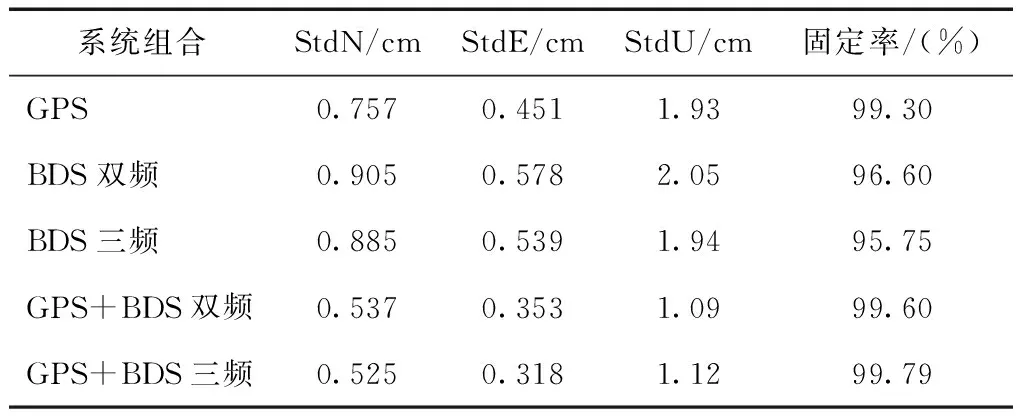
表1 5种定位模式精度统计及固定率

图2～图6给出了5种定位模式生成的BASE4的坐标与已知坐标的差值在UTC 0点至24点的N、E、U方向上的时间序列，表1是5种定位模式的定位精度和固定率统计。可以看出采用非组合模型对于BDS双频和三频数据可以采用同样的方式进行处理，并且在绝大部分情况下均可以得到水平优于1 cm、高程优于3 cm的定位结果。最后采用非组合模型对GPS和BDS双频以及三频分别进行联合处理，由于有更多的可视卫星，其精度和固定率均优于单系统的定位模式。说明本文采用的非组合模型可以对多频多系统数据灵活扩展，并且能够获得水平优于1 cm、高程优于2 cm的定位结果。

2.3 初始化时间

网络RTK的另一个重要服务性能指标是初始化时间，本文所提到的网络RTK服务初始化时间是指网络RTK软件从开始基线解算，到能为用户提供正确、稳定服务所需要的时间，该时间越短则网络RTK服务初始化性能越好。本试验将数据在UTC 0-23 h内每5 min设置一个试验样本，共276个样本数据，不同定位模式的初始化时间统计如表2所示。

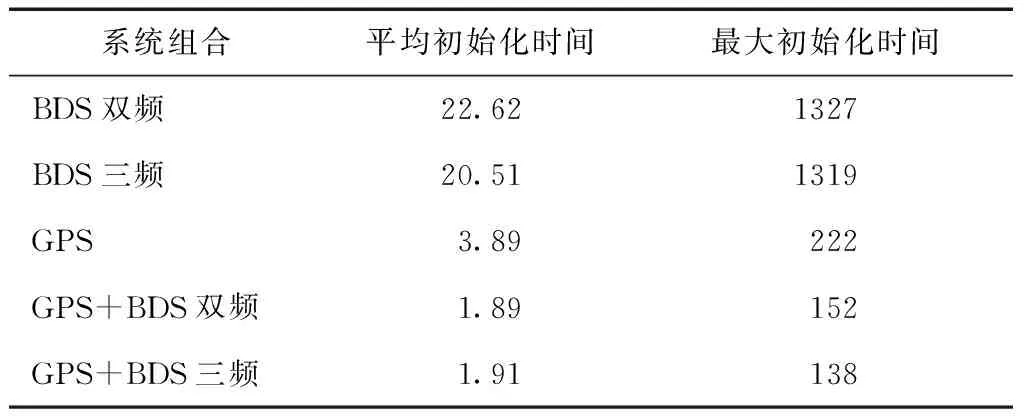
表2 5种定位模式初始化完成时间统计表 s

从表2可以看出：非组合函数模型处理5种定位模式的平均初始化时间均小于30 s，其中BDS双频和BDS三频的平均初始化时间长于其他3种定位模式，并且最大初始化时间也长于其他3种模式。对于单GPS定位模式初始化时间虽然优于BDS系统，但仍比双系统定位模式初始化时间长。将每种定位模式的初始化完成时间按照<30 s、30～60 s、60～300 s和>300 s进行划分，得到5种模式初始化时间的样本数分布，如表3所示。在30 s之内，在85 %以上的样本概率下，5种模式均能完成初始化；对于双系统定位模式，在30 s之内完成初始化的概率更是达到95 %，可以保证网络RTK能够快速、正常提供服务，缩短用户收敛时间。

表35种定位模式初始化完成时间样本个数分布表

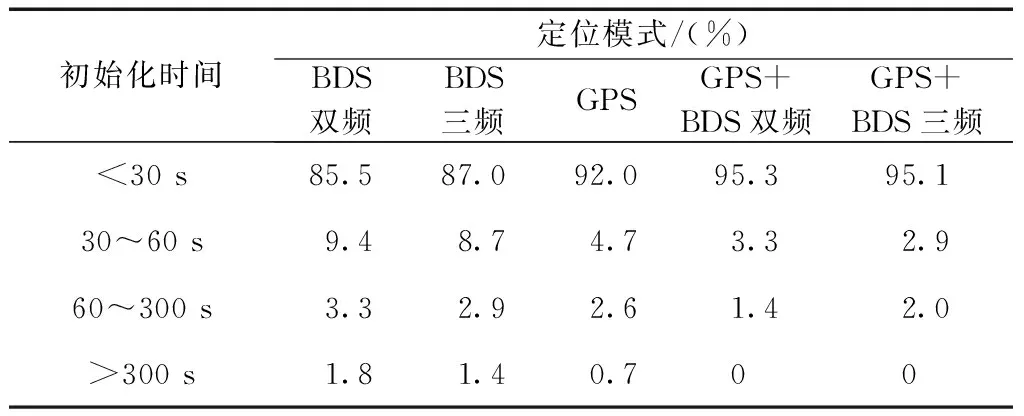
初始化时间定位模式/(%)BDS双频BDS三频GPSGPS+BDS双频GPS+BDS三频<30s85.587.092.095.395.130～60s9.48.74.73.32.960～300s3.32.92.61.42.0>300s1.81.40.700

3 结束语

相对于组合模型，本文提出的非组合模型在数据处理时过程简单，不用分步处理，在网络RTK数据处理中可以直接估计出模糊度参数、电离层参数和对流层参数，并且可以获得水平低于1 cm和高程低于3 cm的定位精度，保证平均初始化时间在30 s以内，能够满足测绘和导航领域内的需求。

对于多频观测值的组合模型，随机模型必须要考虑各个组合观测值误差之间的相关性，增加了处理复杂度。采用非组合模型，不用考虑不同观测值之间组合系数的问题，处理多频观测值更简便，可以同时处理GPS双频及三频数据、BDS双频以及三频数据。

目前，GNSS在不断发展中，将来若出现新的频点载波观测值，可以直接使用本文提出的非组合模型进行处理，扩展性更好。

[1] 高旺，高成发，潘树国，等.北斗三频宽巷组合网络RTK单历元定位方法[J]．测绘学报，2015，44(6)：641-648.

[2] 姚宜斌，胡明贤，许超钤.基于DREAMNET的GPS/BDS/GLONASS多系统网络RTK 定位性能分析[J]．测绘学报，2016，45(9)：1009-1018.

[3] 祝会忠，刘经南，唐卫明，等.长距离网络RTK基准站间整周模糊度单历元确定方法[J]．测绘学报，2012，41(3)：359-365.

[4] 唐卫明，刘经南，陈日高.PowerNetwork软件关键技术介绍和性能分析[J].武汉大学学报(信息科学版)，2008，33(8)：868-871.

[5] 黄丁发，周乐韬，李成钢，等.增强参考站网络RTK算法模型及其实验研究[J].武汉大学学报(信息科学版)，2009，34(11)：1344-1349.

[6] 伍晓勐.网络RTK基站数据处理关键技术研究[D].武汉：武汉大学，2016：23-26.

[7] 王振杰，方稚.GPS数据处理中实时随机模型的估计方法[J].海洋测绘，2014，34(6)：29-31.

[8] 李博峰，葛海波，沈云中.无电离层组合、Uofc和非组合精密单点定位观测模型比较[J].测绘学报，2015，44(7)：734-740.

[9] 高星伟，陈锐志，赵春梅.网络RTK算法研究与实验[J].武汉大学学报(信息科学版)，2009，34(11)：1350-1353.

[10] 唐卫明，刘经南，施闯，等.三步法确定网络RTK基准站双差模糊度[J].武汉大学学报(信息科学版)，2007，32(4)：305-308.

[11] 黄劲松.高精度GNSS数据处理基本数学模型及算法统一理论研究[D].武汉：武汉大学，2012：36-62.

[12] COCARD M，BOURGON S，KAMALI O，et al.A systematic investigation of optmal carrier-phase combinations for modernized triple-frequency GPS[J].Journal of Geodesy，2008，82(92)：555-564.

[13] 祝会忠，徐爱功，高猛，等.BDS网络RTK中距离参考站整周模糊度单历元解算方法[J]．测绘学报，2016，45(1)：50-57.

[14] TEUNISSEN P J G.The least-squares ambiguity decorrelation adjsutment：a method for fast GPS integer ambiguity estimation[J].Journal of Geodesy，1995，70(1-2)：65-82.

[15] CHANG X，YANG Xiaohua，ZHOU Tianyang.MLAMBDA：a modified LAMBDA method for integer least-squares estimation[J].Journal of Geodesy，2005，79(9)：552-565.

Applicationandpositioningperfomanceofun-combinedmodelinGPS/BDSnetwork-RTK

WANGXingbing，HUANGJingsong

(School of Geodesy and Geomatics，Wuhan University/Collaborative Innovation Center for Geospatial Technology，Wuhan 430079，China)

Aiming at the problems that it is complex of the calculation and is difficult to be extended for the combined model in the data processing of network-RTK，the paper proposed a data processing method of un-combined model for GPS/BDS network-RTK，and analyzed its positioning accuracy and initialization time：multiple frequency carrier and pseudorange were used in calculating，and the single-difference ambiguities between base stations，double-difference ionospheric delay and tropospheric delay were estimated.Experimental result showed that the horizontal positioning accuracy of BDS double-frequency and triple-frequency network-RTK would be better than 1 cm(1σexternal accuracy)，the vertical accuracy would be better than 2 cm(1σexternal accuracy)，the positioning accuracy of network RTK for single GPS would be better than that for single BDS，and that for GPS/BDS would be better than that for single GPS and single BDS；moreover，the average initialization time of the un-combined model could be less than 30 seconds in positioning service.

GPS/BDS；network-RTK；un-combined model；data processing；positioning accuracy；initialization time

2017-02-17

国家重点研发计划项目(2016YFB0501803)。

王兴冰(1989—)，男，山东济宁人，硕士研究生，研究方向为高精度卫星导航与网络RTK技术。

王兴冰，黄劲松.GPS/BDS网络RTK非组合模型数据处理方法[J].导航定位学报，2017，5(4)：92-97.(WANG Xingbing，HUANG Jingsong.Application and positioning perfomance of un-combined model in GPS/BDS network-RTK[J].Journal of Navigation and Positioning，2017，5(4)：92-97.)

10.16547/j.cnki.10-1096.20170417.

P228.1

A

2095-4999(2017)04-0092-06