一种卫星数量不足情况下的GPS定位算法
刘志锋,张 鹏,商 曼
(1.广州地铁设计研究院有限公司,广州 510010;2.武汉大学测绘学院,武汉 430079;3.精密工程与工业测量国家测绘地理信息局重点实验室,武汉 430079;4.广州市房地产测绘院,广州 510010
一种卫星数量不足情况下的GPS定位算法
刘志锋1,张 鹏2,3,商 曼4
(1.广州地铁设计研究院有限公司,广州 510010;2.武汉大学测绘学院,武汉 430079;3.精密工程与工业测量国家测绘地理信息局重点实验室,武汉 430079;4.广州市房地产测绘院,广州 510010
针对GPS卫星定位时由于障碍物遮挡等原因只能接收到少于4颗卫星的信号而导致定位精度不高的问题,提出一种卫星数量不足情况下的基于“合成孔径技术”的GPS定位算法:利用载波相位平滑伪距、电子罗盘辅助低精度IMU实现初始对准和航迹推算等方法,结合合成孔径技术实现定位。实验结果表明,该方法可以实现卫星信号数量不足情况下的定位,精度在20 m左右。
惯导;卫星数量不足;GPS定位;合成孔径
0 引言
能否在任何时间、任何地点为任何人提供精确的位置信息,是基于位置的服务(location based service,LBS)性能的评价指标;而卫星定位技术如今已经在导航领域中发挥出重要作用[1]。人们在追求高精度定位的前提下,也开始关注在严苛条件下的定位性能。在开阔地带,卫星定位技术能够实现高精度定位;但是在城市峡谷环境中,高楼大厦和高架桥等设施会遮挡卫星信号进而造成卫星信号频繁中断甚至很多卫星信号接收不到[2],使得接收机的冷启动时首次定位时间(time to first fix,TTFF)显著增加,甚至经常会出现卫星信号不足4颗而完全无法定位的情况,严重影响用户的体验。这使得卫星定位技术面临挑战。
处于移动状态的全球定位系统(global positioning system,GPS)接收机在不同时刻处于不同的空间位置,即使由于障碍物的遮挡导致卫星数量不足或频繁中断,GPS接收机仍然有机会在不同时刻不同位置收集到不同的卫星观测值。当GPS接收机观测到的可见卫星小于4颗无法实现定位时候,移动天线试图接收并保存大于4颗的不同卫星观测值,这样即使每次天线能观测到的卫星数量不足4颗,但是根据数据融合技术仍然可以进行伪距观测值的组合,从而实现定位。
“合成孔径技术”是利用雷达天线与目标的相对运动,把尺寸较小的真实天线孔径用数据处理的方法合成较大的等效天线孔径的雷达。本文借用“合成孔径”的思想,把天线从At运动到Bt+k过程中能观测到的所有卫星的观测值用数据处理的方法融合在一起,将其看作一个“大天线”来进行定位。基于“合成孔径技术”的GPS定位方法广泛适用于由于障碍物的遮挡或接收机的高动态性而导致的卫星数量不足、卫星信号频繁中断的场景,可为提高GPS在卫星数量不足或者频繁中断的情景下的定位算法研究提供参考。
1 基本模块分析与实现
1.1 载波相位平滑伪距
软件接收机相比硬件接收机具有算法更易于升级、扩展性更好和成本较低等优点;本文基于软件接收机平台进行卫星数量不足情况下的定位研究。基于“合成孔径技术”的GPS定位方法利用伪距观测值来实现,接收机直接输出的伪距观测值精度较低,难以满足实验要求;故本文在软件接收上实现了载波相位平滑伪距并将其输出,以提供初始观测值的精度,主要思想是利用精度更高的载波相位观测值来平滑粗糙的伪距观测值[3],以降低伪距观测值的误差,提高定位精度。短时间内,电离层、对流层随时间变化量可以忽略不计,在理想的没有周跳情况下,载波相位历元间差值与伪距历元间差值表示的距离变化量应该相等。以此为前提可以推导载体相位测量值进行伪距平滑的公式,其具体推理过程如下:
t时刻L1相位观测方程为

(1)
那么相邻历元载波相位差分观测值为
λδΦ=λΦt+1-λΦt。
(2)
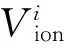
由于相邻历元的接收机钟差、电离层、对流层时延变化量可以忽略不计,将式(2)整理得

(3)
(4)

(5)
1.2 电子罗盘辅助对准
针对卫星数量不足4颗的场景,尝试利用低精度的惯性测量单元(inertial measurement unit,IMU)来辅助接收机定位,IMU能够提供全球卫星导航系统(global navigation satellite system,GNSS)接收机的相对位置变化信息,是正确进行“合成孔径”算法的基础。因为惯导是航迹推算系统,在进行航迹推算时IMU需要先完成航向角的初始对准,才能进行后面的航迹推算工作,而低精度的IMU无法通过自对准得到航向角;因此本文借助电子罗盘来提供初始的航向角。
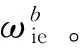
(6)

对式(2)作转置并简单处理,可得[5]
(7)

(8)

(9)

(10)

1.3 低精度惯导更新算法
微机电系统(micro-electro-mechanical system,MEMS)传感器有体积小、价格低、功耗小、使用方便等优点[7],已经成为国内外学者的研究热点。低精度MEMS系统与高精度的惯性导航系统相比,低精度MEMS系统陀螺仪和加速度计的零偏、随机噪声都比较大,陀螺和加速度计的固定零偏误差和零偏飘移误差等导致积分的初始值不为零,对后面所有计算历元都会产生累积误差,严重影响导航定位的结果;所以需要对数据进行预处理,主要包括对数据进行平滑滤波、零偏误差校正等,以尽量得到能够反映载体真实运动信息的数据,然后再进行姿态、速度、位置的更新。
因为IMU输出的陀螺角速度和加速度值都是相对惯性坐标系的测量值,要计算出载体的位移情况并进行导航或者位置推算,更关心的是当地导航坐标系下载体的位移情况;所以需要把比力测量值从载体坐标系投影到导航坐标系[8]。这就需要陀螺仪不断给出载体坐标系到导航坐标系的姿态矩阵,然后去除有害的加速度测量值,比如重力加速度、科氏加速度等等。总结起来,导航方程的求解过程主要分为以下4步:IMU姿态矩阵的更新、比力投影到计算用的导航系、载体在导航坐标系下的速度更新和载体在导航坐标系下的位置更新。其中角速率测量值积分更新姿态为后面的比力投影提供姿态矩阵、比力积分更新速度、速度积分更新位置[9]等。具体算法流程如图1 所示。

图1 MEMS算法流程
2 合成孔径算法
在由于城市峡谷、高楼大厦等的遮挡而导致有效信号的卫星不足4颗的情况下,普通的接收机算法无法实现定位。此时接收机仍然可能取得2或者3颗卫星的观测值,可以利用接收机保存视野下能观测到的小于4颗卫星的观测值;当接收机移动后接收到其他的卫星,同样可以保存下此时的卫星观测值。虽然在2个时刻能观测到的卫星数量都小于4颗,但是可以尝试将2个时刻的小于4颗卫星的观测值结合起来实现定位。简单地说,此算法输入值是不同时刻的小于4颗的卫星观测值和IMU推算的相对位置,输出值则是实时的接收机位置。
利用短时间内同一卫星到接收机之间的伪距观测方程的强相关性和IMU提供的航迹推算相对位置,将不同时刻不同位置的卫星观测值融合起来,以实现不足4颗卫星情形下的特殊场景的定位,这里称这种“合成孔径”算法为“几何法”。此方法不需要接收机初始位置,仍然能够进行虚拟观测值的构建并且实现定位,和单点定位模型很相似;不同之处在于“合成孔径”方法是利用了2个不同时刻的观测方程结合在一起组建而成的。


图2 几何模型

卫星的观测值和t+k时刻能观测到的3颗卫星的观测值,又因为“合成孔径”的时间间隔k通常较短,可近似认为钟差的变化量Δt为零[10];那么t时刻到t+k时刻未知参数的个数仍然为(x,y,z,t)4个,即在t时刻的接收机坐标和钟差只需要列出4个伪距观测方程即可求解得出。
由于“合成孔径”中GPS信号中断时间较短,通常小于1 min,在短时间内卫星钟差、电离层、对流层误差的变化量对定位结果的影响是可以忽略的[10]。而本文的思路是为了解决接收机在完全无法定位情况下的定位问题,即处理10 s以内或小于1 min范围内的卫星中断,而且是利用伪距的定位,可以忽略钟差、电离层误差在短时间内的变化值。如果不采用这种方法,则完全得不到位置;故为了得到卫星数量不足情况下的接收机位置,可以假设在中断的这些时间里各个卫星的钟差、电离层误差、对流层误差变化是可忽略的,可简化为
(11)

(12)

(13)
可以看出t+k时刻3个方程式与前面t时刻2个方程主要差别在于多了一个IMU的航迹推算向量(Δx,Δy,Δz),相当于在计算的常规卫星位置上作了一个改正。根据以上方程式可以列出相应的观测方程,并对其进行线性化,列出间接平差方程Vi=-liVx-miVy-niVz-ctr+Li,式中Vx、Vy、Vz为接收机位置的改正数。其中对t时刻的观测卫星有
(14)

(15)
常数项
(16)
再根据间接平差方程式
V=BX-L,
(17)
其中:V为改正数;B为系数矩阵;X为未知参数(xr,yr,zr,tr);L为常数项矩阵。即可求得未知参数X,得到定位结果,实现卫星信号频繁中断和卫星数量不足情况下的定位。
3 实验与结果分析
为验证“合成孔径”算法的可行性,本文设计实现了静态实验和动态实验。首先是静态静态实验,静态情况下,接收机静态不动,故没有IMU的推算误差,用来与动态实验做对比。
3.1 静态实验
本次实验数据采集于2015-12-28,将2个相同GPS天线分别连接软件接收机和NovAtel测量型接收机Propack-V3,天线放在测绘学院404实验室楼顶,接收机放在404实验室。打开接收机,同步观测约45 min左右,并保存所获得的观测文件和星历文件,得到观测文件并导出。先在RTKLIB软件中观察其卫星高度角、视野中的时间等信息,然后确定并选择模拟实验需要的卫星以及时间段。用TEQC软件对原始数据进行基本处理,对原始数据进行卫星号的剔除和时间上的截取,利用原始观测数据构造模拟成只有3颗卫星的情景来进行后面的实验。
商用接收机几何法定位结果如图3所示,以图中接收机基准位置作为参考真值,而深色点状为计算得到的几何法定位的坐标序列。软件接收机的定位计算方法与商用接收机类似,其定位结果如图4所示,以图中接收机位置为参考真值,而深

图3 商用接收机几何法定位结果

图4 软件接收机几何法定位结果
色点状为计算得到的几何法定位的坐标序列。
可以看出,软件接收机和商用接收机几何法定位精度差别不大,但是存在偏差,大概在20 m左右。
3.2 动态实验
动态实验数据采集于2015-12-28,将IMU、接收机固定在小推车后,先静止放置几分钟,再以中等速度推动小推车,如图5所示。采集到IMU数据后,先对原始数据进行预处理,主要包括对数据进行平滑滤波、固定零偏误差校正等;然后再进行航迹推算,并在谷歌地球软件上画出小推车轨迹,如图6中浅色线所示。可见轨迹误差随着时间推移在发散,但是总共推移了大概只有30 m左右,推动的时间约为40 s。从图中可见IMU总的定位精度大约为5 m左右。

图5 小推车实验

图6 小推车计算轨迹示意
动态实验定位方法与静态实验类似,只是增加了IMU航迹推算的相对位置基线。最终定位结果如图7和图8所示,从图可看出商用接收机几何

图7 动态情况商用接收机几何法定位结果

图8 动态情况软件接收机几何法定位结果
法定位偏差大概有15 m左右,软件接收机几何法定位偏差大概有20 m左右。
4 结束语
本文针对由于障碍物的遮挡导致GPS卫星信号数量不足或频繁中断,可以接收到信号的卫星少于4颗而无法定位的问题,提出了一种基于“合成孔径技术”的GPS定位算法,为卫星数量不足、卫星信号频繁中断的情况提供定位解决方案。最后通过静态实验和动态实验对算法进行验证,结果表明可以实现卫星信号数量不足情况下的定位,精度在20 m左右。
本文的方法也可以用于GPS/IMU组合导航在遮挡严重无法正常初始化时组合导航系统的初始位置确定。
[1] 徐亚明,刘志锋,张鹏,等.USRP平台下GPS软件接收机高精度定位的实现[J].测绘通报,2016(2):8-11.
[2] 张奕然.复杂城市环境下智能车导航定位方法研究[D].成都:电子科技大学,2015:30-35.
[3] 范士杰,孔祥元.基于Hatch滤波的GPS伪距相位平滑及其在单点定位中的应用[J].勘察科学技术,2007(4):40-42.
[4] HATCH R.The synergism of GPS code and carrier measurements[C]//Defense Mapping Agency & National Ocean Survey.Proceedings of the 3rd Geodetic Symposium on Satellite Positioning.Las Cruces:Physical Science Laboratory of the New Mexico State University,1982:1213-1231.
[5] 秦永元.惯性导航[M].北京:科学出版社,2014:90-97.
[6] 鲍其莲,吴周洁.低成本捷联惯导系统初始对准方法[J].中国惯性技术学报,2008,16(5):513-517.
[7] 肖昌怡.基于MEMS的导航系统设计与实现[D].哈尔滨:哈尔滨工程大学,2010:60-63.
[8] CHATFIELD A B.Fundamentals of high accuracy inertial navigation[EB/OL].[2016-11-20].https://www.adpenguin.biz/LP_TA/index.cfm?T=437420.
[9] BUDIYONO A.Principles of GNSS,inertial,and multi-sensor integrated navigation systems[J].Industrial Robot,2012,67(3):191-192.
[10] 曾凡河.基于时间差分的单机单频伪距定位及应用[D].长沙:中南大学,2007:30-33.
AGPSpositioningalgorithminconditionofinsufficientsatellites
LIUZhifeng1,ZHANGPeng2,3,SHANGMan4
(1.Guangzhou Metro Design & Research Institute Co.Ltd.,Guangzhou 510000,China;2.School of Geodesy and Geomatics,Wuhan University,Wuhan 430079,China;3.Key Laboratory of Precise Engineering and Industry Surveying,National Administration of Surveying,Mapping and Geoinformation,Wuhan 430079,China;4.Guangzhou Real Estate Surveying and Mapping Institute,Guangzhou 510010,China)
Aiming at the problem that the accuracy is liable to be lower due to the signal
from less than 4 satellites by obstacle blocking in GPS positioning,the paper proposed a GPS positioning algorithm in the condition of insufficient satellite number based on the synthetic aperture technology:carrier-phase smoothing technology,electronic compass aided low-precision IMU initial alignment and dead reckoning were used,and synthetic aperture algorithm was combined to do the positioning.Experimental result showed that the proposed method could help achieve the positioning by insufficient satelllites with an accuracy around 20 m.
inertial navigation;insufficient satellites;GPS positioning;synthetic aperture
2016-12-30
国家自然科学基金项目(41374011;41474005);湖北省自然科学基金项目(2014CFB717)。
刘志锋(1991—),男,湖北黄石人,硕士,助理勘测师,研究方向为地铁安全监测和GPS软件接收机相关技术。
刘志锋,张鹏,商曼.一种卫星数量不足情况下的GPS定位算法[J].导航定位学报,2017,5(4):10-15.(LIU Zhifeng,ZHANG Peng,SHANG Man.A GPS positioning algorithm in condition of insufficient satellites[J].Journal of Navigation and Positioning,2017,5(4):10-15.)
10.16547/j.cnki.10-1096.20170403.
P228
A
2095-4999(2017)04-0010-06

