例谈提高学生审题能力的有效策略
曹 悦
(东至县至徳小学 安徽池州 247200)
《中国学生发展核心素养》指出,学生核心素养是指学生应具备的,能够适应终身发展和社会发展需要的必备品格和关键能力。面对新时代的教育教学工作,注重发展学生核心素养是每位学科老师所面临的新课题。为此,数学老师也应基于教学实践,着力探究发展学生核心素养的途径和方法。在教学实践中,老师要树立培育学生数学核心素养的理念,找准切入点,探索途径,在一线课堂中不断尝试创新方法,多渠道培养学生灵活多变的数学思想,提升学生的思维能力。
简单来说,学生学习数学的过程就是通过有效数学思维训练形成完整清晰的知识脉络,用数学思维发现和解决生活实际问题,彰显数学文化的育人功效。
亲历一次次教学实践,面对一次次作业反馈,我有这样的迷惑:一堂新课结束后,学生对基础性练习,做起来不碍手,正确率很高。对于提升性乃至开放性练习,错误率却居高不下。刨根究底,审视学生的错误解题方式,发现他们审题能力薄弱,思维能力训练不足,良好的审题习惯有待养成,数学素养有待提升。
为此,在数学学习中,我以提升审题能力为切入点,逐渐提高学生思维能力,落实学生数学核心素养目标。下面,我就结合教学案例,浅谈基于发展学生数学核心素养审题问题及解决策略。
一、审题时出现的问题
在教学实践中,梳理学生审题的薄弱环节,发现学生常有的审题问题有以下三种:
(一)概念模糊不清,审题易出现偏差
数学概念比较抽象,往往难用语言描述,很多时候,它要建立在学生充分理解的基础上,才可融会贯通,举一反三。如对“单位1”“倍数”“小数的意义”等概念性知识的理解,学生需借助实例或生活模型,也需在对比强化中加深理解。
【案例一】学校图书馆现有260本科技书,科技书本数是故事书的2倍,科技书和故事书共有多少本?
解决这题,学生匆忙读题,很快列出算式:260×2+260=780(本)或260×(2+1)=780(本)。追问原因,学生①答:这题很简单,题中出现2倍,所以先用260×2算出科技书的本数,再算出两种书的总本数。学生②答:求科技书和故事书的总本数,就是求科技书本数的3倍是多少?所以列式:260×(2+1)=780(本)。
显然,学生自认为正确的算式是错误的。因为学生对“倍数”概念掌握不牢固,模糊不清,简单认为出现“倍数”字眼,就用乘法解决,没有思考:科技书的本数是故事书的2倍,是指故事书本数是科技书的1/2,也就是说,并不是有“倍数”一词,就用乘法计算。这类的审题障碍,我们称之为“概念模糊不清”,对概念一知半解,势必影响解题效果。
(二)读题不够细致,审题落入陷阱
数学文字题一般短小精炼,不细致读题也容易落入“陷阱”。小学生年龄小,喜欢匆忙看题答题,很难养成仔细读题、认真审题的习惯。一不留神,就掉进题目陷阱,盲目写出错误答案。如遇到单位不统一的两组数据,盲目相加减;遇到题中无用的条件,没有选择性使用等,出现啼笑皆非的错误。
【案例二】有三根小棒,长度分别为5厘米、1分米和6厘米,这些小棒可不可以围成三角形?
解决这道题,学生稍作思考,学生①得出:“这题太简单了,不可以围成。”学生②答:“5+1=6(厘米),两边之和等于第三边长度,所以三根小棒不能围成三角形。”两位同学答完后,同学们点头表示赞同。
针对学生的解题方式,貌似有理有据,追根溯源,学生没有注意5厘米、1分米这两组线段的单位是不统一,不能直接将5厘米与1分米相加,犯了低级错误。这类审题障碍,我们称之为“读题审题不够细致”,忽视培养学生细致读题审题的习惯,会让学生在解题中栽跟头。
(三)数学思维训练不力,理解题意困难
数学教学是数学思维活动的教学,有了思维的数学课堂才是有灵魂的课堂,学生在这样的课堂中思维才能变得更敏锐、更睿智。教学中,发现学生思维能力发展不均衡,有些学生理解辨析能力弱,造成审题困难。
【案例三】张宁和王晓星一共有86张画片,王晓星给张宁8张后,两人画片张数同样多,两人原来各有画片多少张?
解决这道题,学生①轻而易举列出算式:张宁(86-8)÷2=39(张);王晓星39+8=47(张)。学生②阐述解题思路:王晓星给张宁8张后,两人画片张数同样多,也就是王晓星比张宁多8张画片,由此列出算式:(86-8)÷2=39(张)。当学生没有疑问时,老师质疑:王晓星47张,张宁39张,王晓星给张宁8张后,两人的画片张数同样多吗?辨析后,学生知道这种解题方式不正确,但为什么不对,百思不得其解。
针对这样的解题方式,学生不能准确理解“王晓星给张宁8张后,两人的画片张数就同样多”与“王晓星比张宁多8张画片”之间的区别。这样的审题错误,源于学生理解力较弱,没有找到分析题意的好方法,我们称之为“理解题意困难重重”,这样的理解困难症影响解题方式和效果。
学生常见的几种审题障碍,制约学生思维能力的发展。而训练思维能力是培养学生综合能力的核心,也是培养学生核心素养的有效途径。在教学探索中,我针对学生审题过程中出现的问题,积极寻求提高学生思维能力的突破口:
二、提高审题能力的策略
(一)圈一圈关键词,找准切入点
学生解决问题时,要引导他们养成认真读题的习惯,准确读出题中的关键词,找寻主要信息和隐形信息,并圈一圈关键词,找准切入点,扫清拦路虎,正确剖析题意。在圈一圈、画一画的过程中,找出审题关键,发展学生的数学思维能力。
如案例一,学生认真读题后,圈出关键句:“科技书的本数是故事书的2倍。”继续追问学生:“科技书有260本,故事书的本数应是科技书的多少?如何求出故事书的本数呢?”引导学生明晰“科技书的本数是故事书的2倍,也就是故事书的本数是科技书的1/2”,为此,故事书的本数并非520本,应是130本,两本书的总本数为390本。
再看案例二,圈出关键句“长度分别为5厘米、1分米和6厘米”,小手一指,学生明白了这里出现不同的长度单位“厘米”和“分米”。学生立马答道:“单位不统一,不能相加减。”将1分米化为10厘米,单位统一后,再根据“三角形两短边之和大于第三边”进行判断,因为5+6=11(厘米),且11厘米>10厘米,可判定能围成三角形。
看,学生在圈一圈关键词中,提取关键信息,找准解题切入口,明辨解题思路。在这个过程中,学生会逐渐学会分析题意的方法,养成认真析题的习惯,习得融会贯通的能力,思维能力得到提升。
(二)学会画图分析,更准确直观理解题意
学生解决问题时,分析题意的能力有高有低,可鼓励学生用“线段图”“表格”“直观图”等形象方式描述信息,辨析题意。学生在画一画中,借助图形辨析题中隐藏的数量关系,明晰思路和审题策略,提升解决问题的能力。
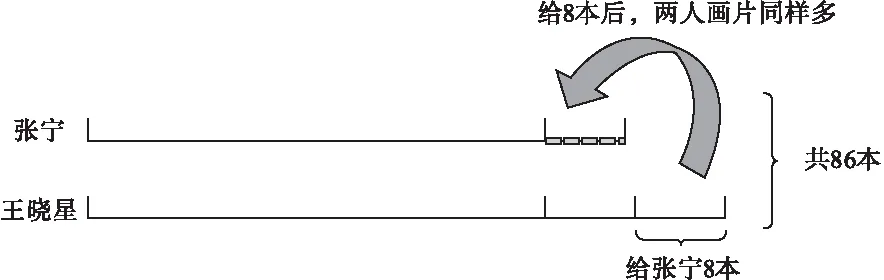
如案例三,可引导学生画“线段图”来辨析题意。
学生①答:王晓星给张宁8张后,两人画片数同样多,那么王晓星原来的画片应比张宁多:2×8=16(张)。学生们豁然开朗,问题迎刃而解,得出列式:张宁(86-2×8)÷2=35(张);王晓星35+16=51(张)。
瞧,用画一画的方式代替枯燥的分析,将复杂数学问题变得简明形象,用最简单易懂的方式解决了难题,学生在“画一画”“说一说”中提升分析、推理及判断能力,思维训练贯穿其中,受益颇丰。
(三)经常辨析相似题,找出异同,明晰审题关键
在实际教学中,老师容易陷入“唯分数论成败”的怪圈,惯用题海战术,提高学习成效。其实,这是教学大忌,这样会制约学生思维发展。我们要树立大教育观,基于提升学生数学核心素养,运用比一比相似题的教学策略,将类似的题目进行梳理归整,引导学生比较异同点,从而明晰不同的解题思路,达到思维训练之目的。
针对案例一易错点,我设计了另一道相似题,将两题放在一起进行比较:
(1)学校图书馆现有260本科技书,科技书本数是故事书的2倍,科技书和故事书共有多少本?
(2)学校图书馆现有260本科技书,故事书本数是科技书的2倍,科技书和故事书共有多少本?
让学生细读题目,认真思考,慢慢有小手举起。学生①说:“这两题既有相同点,又有不同点,第二个条件有所不同。”师追问:“两题的解题方式到底有何不同呢?”启发学生思考,明辨异同后,学生②答:“两道题的思路是相同的,都是先求故事书的本数,但第(1)题得用除法,第(2)题得用乘法。”师追问:“什么时候用乘法,什么时候用除法呢?”在这样对比追问中, 学生奋力寻找异同点,学生③精彩答道:“当‘单位1’知道,用乘法计算;当‘单位1’不知道,用除法计算。”在一步步引导中,达到了“山重水复疑无路,柳暗花明又一村”的境界。
看,在相似题的对比练习中,在思辨推理中,异同点明晰了,思路清晰了,审题能力提升了,思维能力得以训练了。
总之,作为新时代的数学教师,要格外关注培育学生的数学核心素养,摸索探究,提升学生自主学习能力。从提升审题能力入手,在启发、点拨、释疑中,激发学生自主探究热情,灵活运用圈一圈关键词、画一画直观图、比一比类似题等审题策略,点燃学生思维的火花,寻求审题妙招,形成培育学生数学核心素养的基本途径。

