巧用几何性质，优化平面向量计算

☉湖南省衡阳市一中 谭祖荣

巧用几何性质，优化平面向量计算

☉湖南省衡阳市一中 谭祖荣

通常我们把平面向量的运算分为几何运算和代数运算（坐标运算），其难点在几何运算上，灵活应用图形的几何特点与性质，往往是解决问题的关键.

一、在三角形中灵活应用“四线，四心”

例1 已知△ABC中，点D在AB上，CD平分∠ACB.若（ ）.

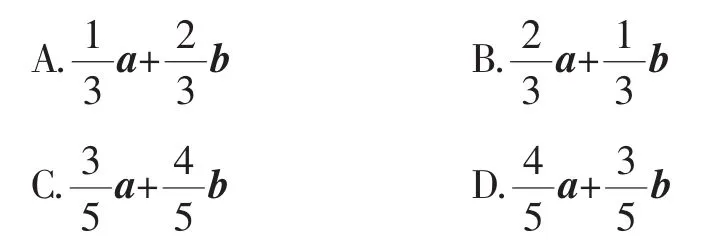
分析：本题是2010年全国卷Ⅱ理数中的试题，主要考查向量的基本运算，考查角平分线定理.

解：因为CD平分∠ACB，由角平分线定理得，所以D为AB的三等分点，且所以故选B.

A.重心 B.外心

C.内心 D.垂心

分析：本题考查了平面向量的加减运算、向量的共线及点的轨迹.

解：如图1，由分别表示上的单位向量，从而

图1

又四边形ADFE为菱形，于是AF平分∠BAC.

A.重心 B.外心

C.内心 D.垂心

分析：本题考查了平面向量的加减运算、向量的共线及点的轨迹.

解：如图2，由AD为BC边上的高，于是

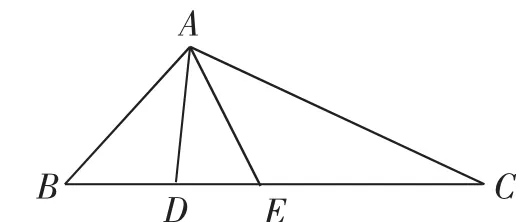
图2

A.重心 B.外心

C.内心 D.垂心

分析：本题考查了平面向量的加减运算、向量的共线及点的轨迹.

解：由

例5在△ABC中，∠A，∠B，∠C的对边分别为a，b，c，重心为G，若a则∠A=________.

分析：本题考查了三角形的重心的性质、平面向量的加减运算及共线向量定理.

解法1：由G是三角形ABC的重心知

解法2：由G是三角形ABC的重心知令于是

二、利用向量的模的几何意义构建几何图形

例6 已知平面向量α，β（α≠0，α≠β）满足|β|=1，且α与β-α的夹角为120°，则|α|的取值范围是__________.

分析：本题是2010年浙江理数中的试题，主要考查了平面向量的四则运算及其几何意义，突出考查了对问题的转化能力和数形结合的能力，把题设条件表示在三角形中，即可迎刃而解.

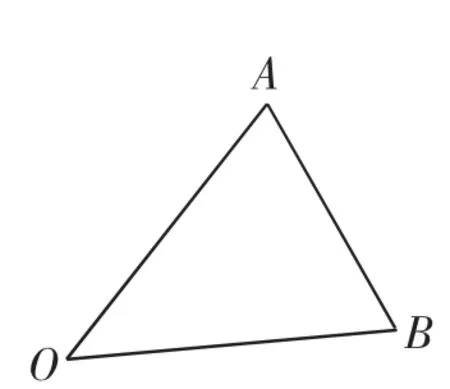
图3

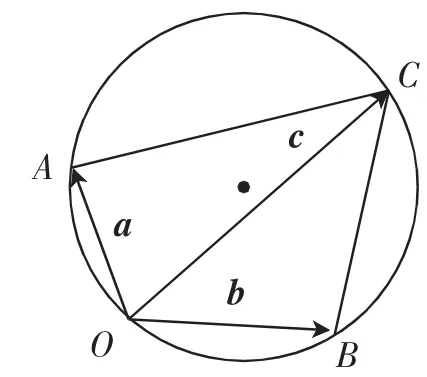
图4

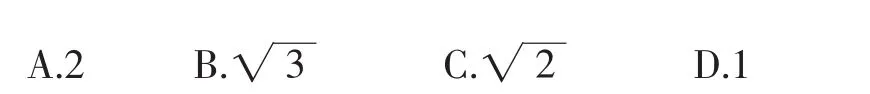
分析：本题是2011年全国大纲卷理数中的试题，考查平面向量的知识，与2010年浙江理数试题相同，更突出考查了对问题的转化能力和数形结合的能力，利用题设条件及其几何意义把问题转化到三角形的外接圆中，应用几何方法求最值.

通过以上几个示例启示我们：在向量的几何运算及与模有关问题中，通过转化与化归，灵活应用图形的几何特点与性质可让问题迎刃而解.