加强数学解题中“数”的研究，提高学生的核心素养

☉江苏省金湖中学 陈万斌

加强数学解题中“数”的研究，提高学生的核心素养

☉江苏省金湖中学 陈万斌

“数”是数学的基础和核心，是数学中最基本、最重要的呈现方式，可以说没有“数”就没有数学.学生对“数”的认识是最基本的数学素养，这就需要我们在教学或解题指导中加强对“数”的本质及特征性研究，加强“数”在具体习题中的实际用意和数学含义的思考.针对性对“数”进行专题探讨，提高学生灵活思维能力和分析问题、解决问题的实践能力，通过对“数”的研讨，不断提高学生的数学核心素养.下面从几个例题来加以说明.

一、“系数”在圆锥曲线中的运用，培养学生的直观想象素养

例1已知（x0，y0）是椭圆上一点，A（1，1），点F为其右焦点，求（|PA|+2|PF|）min.

解析：抓住数字“2”的实际含义和用法.设过点P作右准线的垂线，垂足为N.

故（|PA|+2|PF|）min=（|PA|+|PN|）min=|AN|=4-1=3.

评论：抓住数字“2”的实际含义和用法，联想离心率直接转化.

二、“变数”在不等式中的运用，培养学生的数学抽象素养

例2定义R上的函数（fx）是奇函数，当x≥0时，（fx）=x2对任意x∈［t，t+2］，不等式（fx+1）≥2（fx）恒成立，求实数t的范围.

解析：解题在于试题中“2（fx）”中数字“2”变到“自变量中”去.由（fx）是奇函数知，故2（fx）=又（fx）是R上增函数，原不等式：当x∈［t，t+2］时恒成立，即当恒成立，即

评论：解题在于试题中“2（fx）”中数字“2”变到“自变量中”去，培养学生对函数抽象化的理解.

三、“拆数”在三角函数中的运用，培养学生的数学运算素养

例3已知sin（3α+β）=2sin（α+β），求的值.

解析：比较已知与结论，抓住“3”和“1”处理：3=2+1，1=2-1.

因为3α+β=（2α+β）+α，α+β=（2α+β）-α，

则由已知得sin［（2α+β）+α］=2sin［（2α+β）-α］，

即sin（2α+β）cosα+cos（2α+β）sinα=2［sin（2α+β）cosα-cos（2α+β）sinα］，

于是sin（2α+β）cosα=3cos（2α+β）sinα，故

评论：培养学生善于观察“数”，把握运算技巧.

四、“常数”在函数单调性中的运用，培养学生的逻辑推理素养

例4已知定义域为（0，+∞）的单调函数（fx），若对任意x∈（0，+∞），都有则方程（fx）=2+的解的个数是（ ）.

（A）3 （B）2 （C）1 （D）0

解析：抓住关键词，充分理解题目的本质.本题关键词是“单调”，函数f（x）在（0，+∞）上是单调的，再由知，（fx）+log1x只能是一个“常数”.

2

则log2m+m=3，

故m=2.

故（fx）=log2x+2.

所以x1=4或x2=16共两解.

评论：抓住关键词充分理解题目的本质，进行逻辑推理.

五、“凑数”在函数最值中的运用，培养学生的数学建模素养

例5已知求（fx）的最大值和最小值之和.

解析：分析已知函数特点，进行变化.

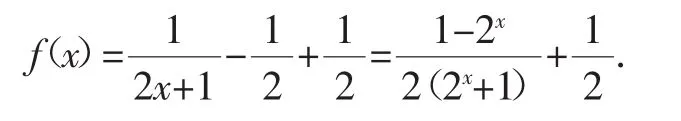
maxmin

评论：由常见结论是奇函数，故配数可解题.分析已知函数特点，建立新的函数模型.

六、“消数”在圆中的运用，培养学生的数据分析素养

例6已知点M在圆C：（x-4）2+（y-4）2=8上运动，A（6，-1），O为原点，求数S=（|MO|+2|MA|）min

解析：本题的难处在于式子“|MO|+2|MA|”中的数字“2”如何“消去”.设M（x0，y0），则（x0-4）2+（y0-4）2=8，

设点B（3，3），则S=2（|MB|+|MA|），

评论：本题的难点在于“|MO|+2|MA|”中的数字“2”如何“消去”，要善于捕捉数据的特点并进行分析和转化.

七、“巧数”在数列中的运算，培养学生对“数”的深层理解

例7已知｛an｝成等比数列，an＞0，a1a5=64，S5-S3=48.

（1）求an；

（2）对于正整数k，m，（lk＜m＜l），求证：m=k+1且l=k+3是5ak，am，al这三项适当排序后能构成等差数列成立的充要条件.

解析：（1）可知an=2n.

（2）证明可知｛an｝中任何不同三项不可能成等差数列（证明略），由数字“5”进行变化，抓住“5”这个“巧数”进行奇偶性推论.

①由2am=5ak+al，则则不成立；

②2a1=5ak+am，同理可得不成立；

③2ak=am+al，得5=2m-k-1+2l-k-1，

评论：对数字“5”的奇偶性及相关式子进行深层次分析.

要活化学生的数学素养，正如在水中才能学会游泳一样，唯有教师引导学生参与课堂，日积月累，才能是显性的思维活动内化为隐形的数学素养，而加强对“数”的特点进行研究，本身培养学生的数学核心素养的一个重要方式、具体手段，教师要在平时教学过程中不断引导学生在数学学习中注意回归到本身、本质，注意回归数学的基础、源头，学生就能更好理解数学的本来面目，更能灵活地分析问题，更能培养学生分析解题能力，更能提高学生的解题能力，进而达到适应试题变化、思考方向的转化要求最大化，达到方法和思维的最优化，达到数学素养提升的最快化.