一道数学竞赛题的解法探究

☉华中科技大学附属中学 曾昀敏

一道数学竞赛题的解法探究

☉华中科技大学附属中学 曾昀敏

一题多解常常训练学生的综合能力，提高他们的数学思维水平，笔者结合2016年全国高中数学联赛湖北省预赛试题第9题谈谈一题多解.

题目：已知MN是边长为的等边△ABC的外接圆的一条动弦，MN=4，P为△ABC的边上的动点，则的最大值为_________.

方法一（基底法1）：以M为起点.，当且仅当也就是P与MN中点H重合时取到等号.

方法二（基底法2）：以△ABC外接圆的圆心O为起点.

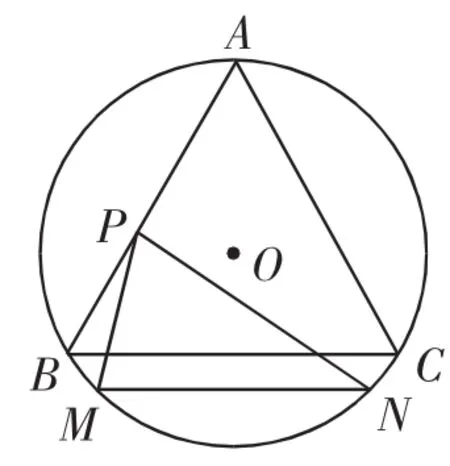
图1

方法三（坐标法1）：以△ABC为参照物，弦MN绕圆心运动.

所以，在△OMN中，OM⊥ON，以△ABC的外心为原点，以BC的中垂线为y轴，建立如图2所示的平面直角坐标系，不妨设点P在BC边上，则因为OM⊥ON，所以可设

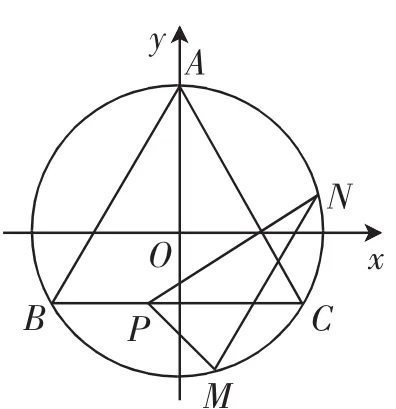
图2

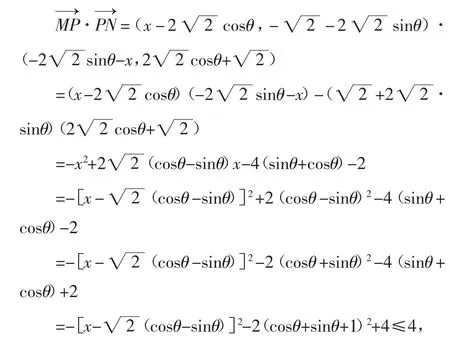
方法四（坐标法2）：以弦MN为参照物，△ABC绕圆心运动.由正弦定理知

又MN=4，则在△OMN中，OM⊥ON.

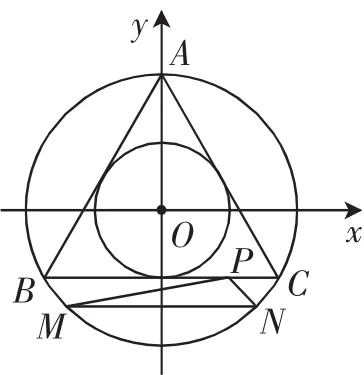
图3

以△ABC的外心为原点，以MN的中垂线为y轴，建立如图3所示的平面直角坐标系.

当且仅当sinθ=-1且r=2，即P（0，-2）时，取到等号.

方法五（不等式法）

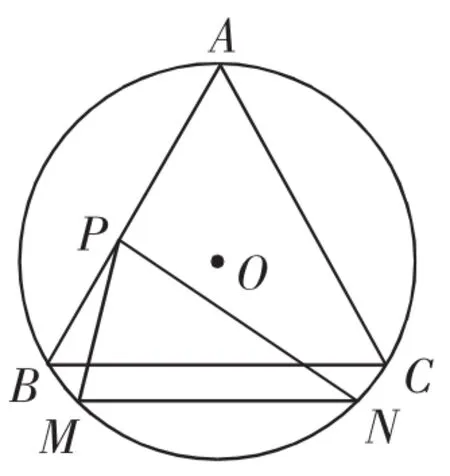
图4

方法六（向量积化恒等式法）：设MN中点为H，则

当且仅当P，H重合时取到等号.因为圆心到△ABC边长的距离，而圆心到MN距离为2，

所以P，H可以重合，即能取到最大值4.

该问题的本质：若两个向量之和的模为定值，当且仅当这两个向量相等时，数量积有最大值_______.

在该题的解法中，我们提出了基底法、坐标法、不等式法、向量积化恒等式法等六种解法，并指出该问题的本质为若两个向量之和的模为定值，当且仅当这两个向量相等时，数量积有最大值.由此，该问题还可以进一步抽象化.通过一题多解，锻炼学生综合运用各种知识的能力，达到事半功倍的效果.