复合函数的零点问题方法探究

☉天津市耀华中学 明廷军

复合函数的零点问题方法探究

☉天津市耀华中学 明廷军

复合函数的零点问题是近些年高考的热点和难点，在全国各地的高考模拟试题中也频频出现，因为它涉及内外多层函数，函数的图像不像基本函数那么简单，所以学生很难掌握，甚至有学生见到这种题就直接放弃，从来不敢奢求做对.正是基于复合函数的零点问题具有综合性强、关系复杂的特点，本文从函数方程、数形结合、分类讨论和化归与转化等数学思想入手，通过例题分析，方法归纳，帮助学生对这类问题进行解读，从而提高学生的数学能力.

一、换元法

（A）（-∞，3） （B）（0，3］

（C）［0，3］ （D）（0，3）

解：令f（x）=t，则t2-bt+c=0.①

要使原方程有8个不同实根，则方程①必有两个不等根t1，t2，且t1，t2∈（0，1］，如图1，函数y1=f（x）与y2=t图像交点的横坐标即为原方程的根.

例1已知函数f

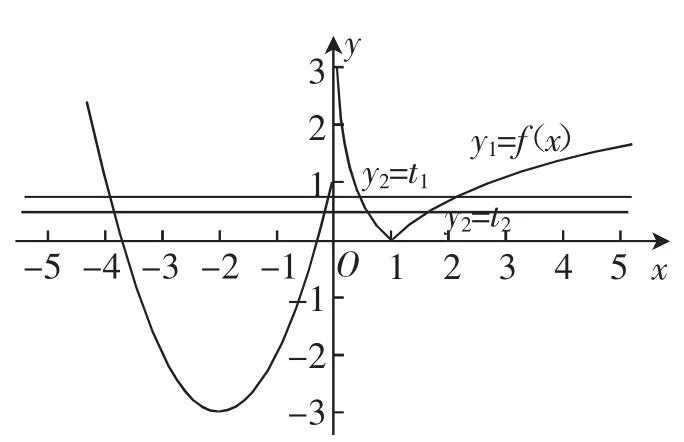
图1

所以b+c∈（0，3）.

小结：利用换元的思想将原来非常复杂的方程转化为学生熟悉的一元二次方程以及大家熟知的基本函数，利用函数图像，问题迎刃而解.

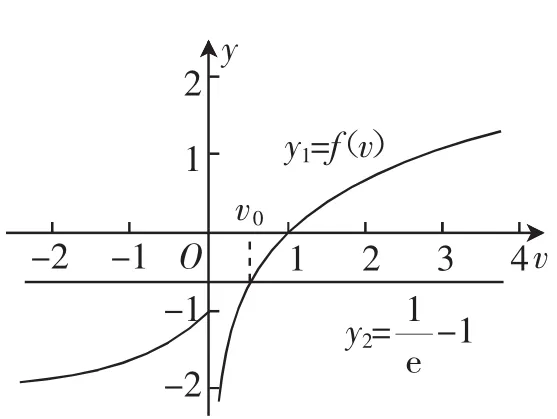
图2

（A）当k＞0时，有3个零点；当k＜0时，有4个零点

（B）当k＞0时，有4个零点；当k＜0时，有3个零点

（C）无论k为何值，均有3个零点

（D）无论k为何值，均有4个零点

解：令f［f（kx）+1］+1=0，则f［f（kx）+1］=-1.

其中v0∈（0，1），所以kx=v0，所以

综上可知，当k≠0时，原函数均有3个零点.

小结：这道题条件虽然很简单，但是让人感觉非常的抽象，因为对于这个函数的图像无从把握，我们依旧遵循了之前先外后内逐层分析的思路，采用了换元的方法，问题得到顺利解决.

二、化归法

例3函数f（x）=-x2+3x+a，g（x）=2x-x2，若f［g（x）］≥0对x∈［0，1］恒成立，则实数a的取值范围是（ ）.

（A）［-2，+∞） （B）［-ln2，+∞）

解：因为g（x）=2x-x2，所以g（′x）=2xln2-2x.

因为［g（′x）］′=（2xln2-2x）′=2（xln2）2-2，ln2＜1，所以（ln2）2＜1.

所以当x∈［0，1］时，2（xln2）2-2＜0，即［g（′x）］′＜0，所以g（′x）在［0，1］上单调递减.

所以g（x）在［0，1］上先增后减，且g（0）=g（1）=1，所以g（x）≥g（1）=g（0）=1.

又因为x∈［0，1］时，2x-x2≤2x≤2，所以g（x）∈［1，2］.

所以原不等式可等价于［fg（x）］min≥0，

所以a≥-2.

小结：利用导数分析内层函数的单调性，再结合外层函数的特点，将恒成立问题转化成最值问题，从而便于学生理解和接受.

三、数形结合、分类讨论法

（A）5 （B）6 （C）7 （D）8

解：令，① 则（ft）=a.②

于是，原方程的实根可以分两步来求，先求出方程②的解（y1=（ft）与y2=a的交点横坐标），然后代入到①中，得到最终的解

y=（fx）亦即y=（ft）的图像如图3.

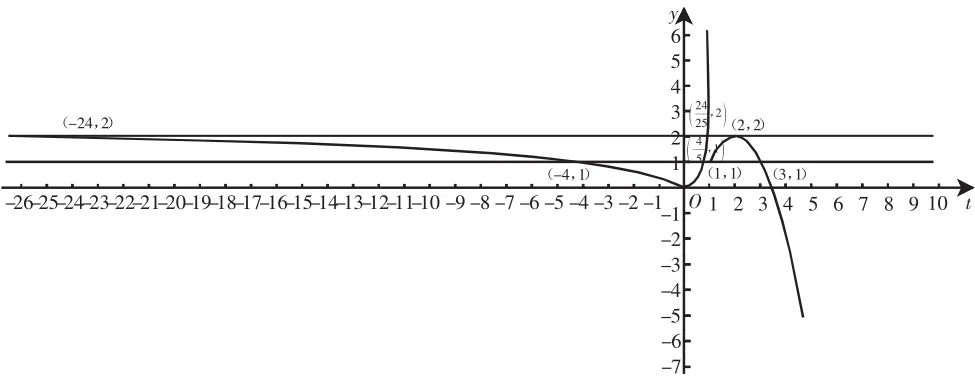
图3

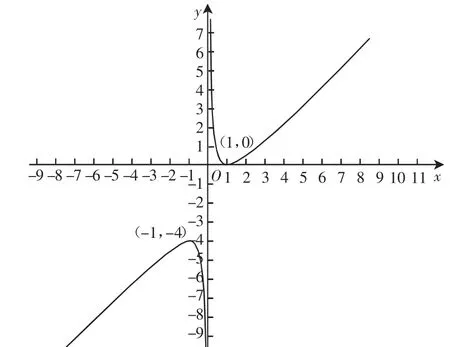
图4

当a＞2时，方程（ft）=a有两个解，分别为t1和t2，其中同时作出与y=t的图像，会发4现它们共有4个交点，即原方程实根个数是4.

当a=2时，方程（ft）=a有三个解，分别为t1，t2和t3，其中同时作出与y=t的图像，会4发现它们共有6个交点，即原方程实根个数是6.

当1＜a＜2时，方程（ft）=a有四个解，分别为t1，t2，t3和t4，其中.同时作出y=x+3与y=t的图像，会发现它们共有8个交点，即原方程4实根个数是8.

当a=1时，方程（ft）=a有四个解，分别为t1，t2，t3和t4，其中同时作出与y=t的图4像，会发现它们共有7个交点，即原方程实根个数是7.

当0＜a＜1时，方程（ft）=a有三个解，分别为t1，t2和t3，其中.同时作出与y4=t的图像，会发现它们共有4个交点，即原方程实根个数是4.

当a=0时，方程（ft）=a有两个解，分别为t1和t2，其中t1=.同时作出与y4=t的图像，会发现它们共有3个交点，即原方程实根个数是3.

当a＜0时，方程（ft）=a有一个解，为t1，其中同时作出与y=t的图像，会发现它们共有2个4交点，即原方程实根个数是2.

综上可知，答案为A.

小结：经过一段时间的学习和思维训练，部分学生对于这类问题会有一些思路和想法，但是准确度却是一个大问题.有的学生花了很长时间，但最后还是功亏一篑.因为学生对于复杂问题的分类讨论并不擅长，但是如果掌握了问题的规律与本质，那么分类讨论就会成为一件非常简单的事情.

例5已知函数则下列关于函数y=f［f（x）］+1的零点个数的判断正确的是（）.

（A）当k＞0时，有3个零点，当k＜0时，有2个零点

（B）当k＞0时，有4个零点，当k＜0时，有1个零点

（C）无论k为何值，均有2个零点

（D）无论k为何值，均有4个零点

解：令t=f（x），①则f（t）=-1，②

所以原方程的实根可以分两步来求，先求出方程②的解（y1=f（t）与y2=-1的交点横坐标），然后代入到①中，得到最终的解（y3=f（x）与y4=t的交点横坐标）.

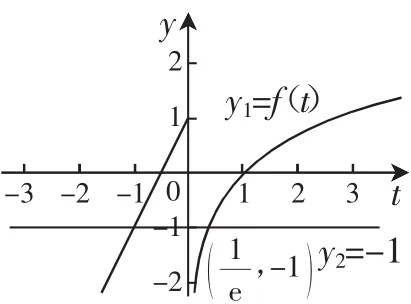
图5

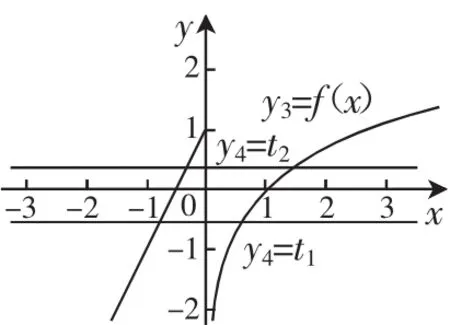
图6

当k＞0时，方程（ft）=-1有两个解，分别为t1和t2，其中；再同时作出y=（fx）与y=t的图像（如图6），会34发现它们共有4个交点，即原函数有4个零点.

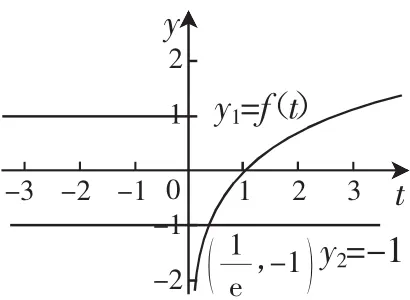
图7

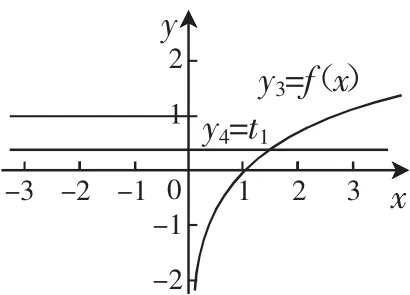
图8

当k=0时，方程（ft）=-1有一个解，为t1，其中；再同时作出y3=（fx）与y4=t的图像（如图8），会发现它们共有1个交点，即原函数有1个零点.

当k＜0时，如图9，

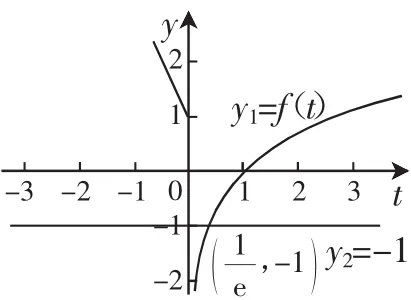
图9

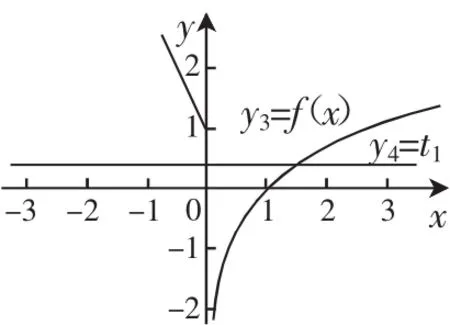
图10

方程（ft）=-1有一个解，为t1，其中；再同时作出y3=（fx）与y4=t的图像（如图10），会发现它们共有1个交点，即原函数有1个零点.

综上可知，答案为B.

小结：这道题的分析思路与方法与上一道题有类似的地方，当你了解了这道题的解法后，你会不得不佩服命题人，他命题时想尽一切办法在那里遮遮掩掩，把一些本来特别简单的问题变得面目全非，故意为难你，目的就是不让学生一下子看出来.所以对于数学的深度学习必须配以深度的理解，学生成绩的提高靠的是学生自己的探究与体悟，绝不是靠课上老师多讲几道题或课下多做几道题就可以实现的.

总之，虽然复合函数的零点问题往往会出现在选择题或是填空题的最后一道题上，是小题中的压轴题，难度非常大，但是从以上例子的分析我们可以得知：如果我们能够利用函数图像从外到内依次进行分析，把握每一个具体函数的特点，那么我们就会大大节省分析问题的时间，提高正确率，将这类问题轻松解决.