基于目标状态的自适应卡尔曼滤波器

高 焘，崔威威，袁剑华，王善民

(1. 海军驻武汉四六一厂军事代表室， 武汉 430000；2. 中国船舶重工集团公司第七二四研究所，南京 211153)

基于目标状态的自适应卡尔曼滤波器

高 焘1，崔威威2，袁剑华2，王善民2

(1. 海军驻武汉四六一厂军事代表室， 武汉 430000；2. 中国船舶重工集团公司第七二四研究所，南京 211153)

针对过程误差难以确定、观测精度较差、目标位置较远时卡尔曼滤波性能下降的情况，结合目标当前运动状态，定义了基于当前观测值置信度的权重矩阵，推导了基于权重矩阵的修正卡尔曼滤波观测更新方程，实现目标状态协方差矩阵、增益矩阵快速自适应调整，提高了算法稳健性。实验验证了算法的可行性和改进性。

目标跟踪；卡尔曼滤波；自适应滤波

0 引 言

目标数据处理是自动控制、航空/航天、雷达数据处理的重要研究课题[1]，研究对象是存在随机干扰的观测数据。因具备无偏最小方差估计以及线性递推的优点，卡尔曼滤波器在目标跟踪数据处理领域得到了广泛的应用。卡尔曼滤波器面临的主要困难包括难以获得目标运动的先验信息，观测噪声会随着环境、天气和设备状态不同而变化，过程噪声也需要进行相应的调整。但是，对过程噪声进行精确的分析的算法计算复杂[2]，实践中假定过程噪声和观测噪声是互不相关的，并使用有界噪声模型。[3-5]

在过程噪声模型难以确定情况下，存在卡尔曼滤波器发散、滤波性能下降等问题，尤其在观测精度不高、目标速度低条件下，错误的过程模型会严重影响目标状态估计。卡尔曼滤波器获得相当广泛的研究和改进以增强滤波稳健性和自适应性。王文正等人给出了一类表征过程噪声模型优劣的简便算法[6]，但依赖最小上界的选取，难以做到自适应。周宏仁基于最大最小加速度假设提出了当前统计模型对目标的状态协方差矩阵进行调整，增强了目标机动情况下目标跟踪的能力。[7]朱洪艳基于交互多模型算法结合多扫描观测信息，采用离散优化技术，给出了近似于实际过程噪声水平的最优子集模型集。[8]刘建书基于何衍等人的工作，结合模糊推理系统给出过程噪声的调整算法，提升了对目标的跟踪能力。[9]田俊林等人基于周东华提出的强跟踪滤波器[10]，引入了时变渐消因子来尝试修正过程噪声以及状态协方差矩阵，拓展了卡尔曼滤波器在非定轨目标跟踪的应用。[11]相关作者深入研究的成果为本文提供了研究思路和参照依据。

1 标准卡尔曼滤波器

标准卡尔曼滤波器的二维空间目标运动方程和观测方程分别是

xk=Fk-1xk-1+wk

yk=Hkxk+νk

其中，xk=(Xx,vxk,Xy,vyk)表示k时刻目标的位x、y坐标及其速度；wk是零均值白噪声过程的误差序列，其方差矩阵是Qk；vk是零均值白噪声序列，其方差矩阵为Rk；xk的协方差矩阵记为Pk；Fk-1、Hk、Kk表示转移矩阵、观测矩阵和增益矩阵。

根据上述的运动模型和观测模型，卡尔曼滤波算法可以描述如下：

(1) 时间更新

(2) 观测更新

-、+分别表示时间更新结果和观测更新结果，对于观测的目标状态更新，可以进一步写为

2 基于当前状态的卡尔曼滤波器

卡尔曼滤波器的增益Kk将当前观测误差、过程误差引入当前目标状态估计值，决定了滤波器的带宽和反应速度以及滤波效果。较小的卡尔曼滤波器增益能够对非机动状态起到良好的降噪作用，而较大的卡尔曼增益能够对目标机动做出快速反应。标准卡尔曼滤波器中，过程噪声和观测噪声对当前状态估计作出了共同的贡献，在观测精度较差、目标位置较远以及噪声模型和真实情况存在偏差等情况下会出现滤波能力下降。

在观测误差较差、难以准确获得过程噪声的信息情况下，将观测先验信息、目标运动后验信息结合起来，通过定义基于置信度的权重矩阵，实时调整增益矩阵、目标状态协方差矩阵，有助于降低由观测噪声引起的目标状态起伏，增强卡尔曼滤波的稳健性和自适应性：

其中Bk被定义为由观测信息和目标运动后验信息共同决定的权重矩阵。该矩阵描述了目标观测值和目标状态之间的匹配程度。特别针对雷达观测目标，观测值(方位、距离)服从正态分布，因此利用外推位置和观测值之间的方位、距离差计算关联点和外推点之间的置信度λk，此处定义权重矩阵Bk=λkI，也可以使用其他方式权重矩阵计算方式：

式中，σa、σd分别表示方位、距离误差均方根，λa、λd表示目标外推和观测位置的方位、距离差。使用取小是为了避免Bk=λkI矩阵值太小，产生滤波失败的情况。基于修正权重矩阵Bk进一步推导出噪声协方差矩阵、增益矩阵的计算。

由协方差的定义可知：

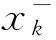
得到

考虑到增益矩阵Kk是使代价函数取得最小值的最优解，通过对矩阵进行微分得到Kk的推导公式：

使上式为0得到

代入状态更新公式：

在实验中，为简化问题以及降低计算复杂度，考虑Bk=λkI，可知计算过程中使用λk等同于Bk，因此使用λk替代Bk：

考虑使用目标滤波前后的状态变化作为过程误差的近似形式在试验中使用如下的状态补偿公式，即使用目标的外推位置和滤波位置距离差作为补偿因子。

3 仿真验证

本文考虑低速条件下的两种运动方式：直线运动和圆周运动。对处于匀速直线运动状态的目标进行滤波试验分析，能够检验滤波器的收敛和平滑性能。对处于圆周运动状态的目标进行滤波试验分析，能够检验滤波器对机动状态的反应速度。设置雷达的方位距、离观测精度分别是0.2°和50 m，设置一个目标以5 m/s的速度，从坐标(60 000,70 000)(单位：m)的位置向240°方向匀速运动300 s后，开始以w=2°s-1法向加速度(对应的法向加速度an=0.1745 ms-2)保持做圆周运动500 s，继续保持直线运动200 s，进行1000次蒙特卡洛仿真实验，得到图1的滤波结果。图中左侧表示改进后的滤波结果，右侧表示标准卡尔曼滤波结果。

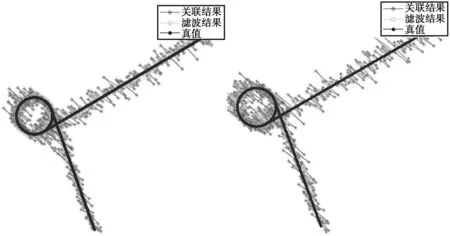
图1 目标跟踪全局

从图1可以看出，改进后的算法滤波位置抖动较小，而标准卡尔曼滤波抖动较大。在前面若干周期内，在观测精度较差条件下，目标的速度难以准确建立起来，需要大约30个周期才能获得较为准确的当前目标速度，在目标速度估计中存在相应的反映。本文考虑目标的位置和速度作为分析指标。首先给出直观的统计结果，如图2、3所示。

图2 XY坐标跟踪误差

图3 XY速度滤波精度

从图2、3可以看出，改进后的算法误差分布范围较小，较为集中，说明算法滤波结果有一定的提升。按照目标的运动特征，将运动过程分为3部分：运动全程、直线运动阶段和圆周运动阶段。3个运动阶段指标的蒙特卡洛仿真统计值如以下3个表所示。

表1 全过运动程跟踪精度表

表2 直线运动阶段跟踪精度表

表3 圆周运动阶段跟踪精度表

从上面3个表格看出，标准卡尔曼滤波器在3种情况下得到的指标值近似，改进后的算法在圆周运动时指标略有下降，除了距离均方根误差外其余指标均有所提升，具体表现为指标的均方根误差小于标准卡尔曼滤波器的均方根误差，尤其是目标的速度和XY坐标滤波。

实验分析表明，当前状态估计增强了卡尔曼滤波器的自适应性，提高了卡尔曼滤波器的滤波效果，同时没有花费更多的计算资源。

4 结束语

针对卡尔曼滤波系统在噪声模型不匹配，以及处理观测精度较差、距离较远的低速目标时跟踪性能下降，基于观测信息和目标运动后验信息给出了一类新算法，该算法能够根据观测值自动调整增益矩阵以及协方差矩阵，增强了算法的稳健性，同时取得了较标准卡尔曼滤波算法更好的跟踪效果。但是，该算法存在目标机动时跟踪指标存在下降的情况，下一步会针对提高目标在高速机动时的跟踪性能做进一步的研究。

[1] Dan Simon. 最优状态估计[M]. 北京：国防工业出版社, 2012: 88-100.

[2] 陈嘉鸿, 韩九强, 席震东, 等. 一般相关噪声下多传感器平滑融合算法[J]. 自动化学报, 2009,35(5):491-497.

[3] 符安迪, 朱云民. 过程噪声和量测噪声多步相关的卡尔曼型滤波[J]. 四川大学学报(自然科学版), 2009, 46(5): 1237-1240.

[4] 李昇平. 过程噪声未知但有界情况下系统最优滤波其设计方法[J]. 电子学报, 2004,32(6): 1050-1053.

[5] 周振威, 方海涛. 在不准确方差下带随即系数矩阵的卡尔曼滤波稳定性[J]. 自动化学报, 2013,39(1):43-52.

[6] 王文正. 基于最小噪声确定模型的结构[J]. 自动化学报, 1999, 25(2): 1-4.

[7] 周宏仁. 机动目标当前统计模型与自适应算法[J]. 航空学报, 4(3):73-86.

[8] 朱洪艳, 韩红, 韩崇昭, 等. 一种改进的多模型噪声识别方法[J]. 系统仿真学报, 2003,15(6): 800-803.

[9] 刘建书, 何亚娟, 王小永, 等. 模糊自适应机动目标跟踪算法[J]. 弹箭与制导学报, 2010.8, 30(4)：8-9.

[10] 田俊林, 付承毓, 唐涛, 等. 过程噪声方差实时补偿的费定轨目标跟踪[J]. 光电工程, 2012，39(1)：68-72.

[11] 周东华, 王庆林. 有色噪声干扰的非线性系统前跟踪滤波[J]. 北京理工大学学报, 1997, 17(3)：321-326.

Adaptive Kalman filter based on target status

GAO Tao1, CUI Wei-wei2, YUAN Jian-hua2, WANG Shan-min2

(1.Military Representatives Office of the PLA Navy in No. 461 Factory in Wuhan, Wuhan 430000;2. No. 724 Research Institute of CSIC, Nanjing 211153)

In view of the difficulty of determining the process error, the poor observation accuracy and the performance degradation of the Kalman filtering when the target position is relatively far, in combination with the current target movement status, the weight matrix is defined based on the current confidence coefficient of the observation value, and the updated observation equations of the modified Kalman filtering are derived based on the weight matrix, realizing the covariance matrix of the target status and rapid adaptive adjustment of the gain matrix, and improving the robustness of the algorithm. The feasibility and improvement of the algorithm are verified via the test.

target tracking; Kalman filtering; adaptive filtering

TN713

A

1009-0401(2017)04-0011-04

2017-10-11；

2017-10-20

高焘(1983-)，男，工程师，研究方向：船舶制造、船舶特种装备仪器；崔威威(1987-),男，工程师，硕士，研究方向：雷达数据处理；袁剑华(1984-),男，高级工程师，硕士，研究方向：雷达系统应用处理；王善民(1986-)，工程师，硕士，研究方向：雷达数据处理。