地铁隧道竖井间贯通测量误差分析与应用研究

胡玉祥，张洪德，王智，孙晓丽

(青岛市勘察测绘研究院，山东 青岛 266032)

地铁隧道竖井间贯通测量误差分析与应用研究

胡玉祥*，张洪德，王智，孙晓丽

(青岛市勘察测绘研究院，山东 青岛 266032)

竖井间贯通测量是地铁隧道施工的重点和难点，因而探索适合城市地铁工程特点的贯通测量技术措施至关重要，本文根据隧道贯通测量的基本工艺流程，在分析贯通测量主要误差源的基础上，对联系测量和地下导线测量两个重要环节进行误差分析和精度预估，提出了适合青岛地铁自身实际的测量精度保证措施，通过实际工程验证，取得了较好的效果。

竖井贯通测量；误差分析；精度预估；联系测量；地下导线测量；青岛地铁

1 引 言

地铁结构施工中，通过精确测量使隧道两个相向施工的贯通面、单向施工的贯通面与预留面的施工中线理想衔接。隧道工程施工一般是由两侧竖井相向推进至贯通面结束，因而在推进线路的纵向、横向和竖向会出现测量误差，其中横向误差和竖向误差对隧道的贯通影响巨大，已有隧道工程贯通测量结果表明竖向贯通误差容易控制[1，2，5]，因而控制好横向贯通误差成为关键。按照规范要求[4]，对于隧道贯通项目要进行贯通误差预计，做好关键环节的设计和控制。本文从青岛地铁隧道实际出发，分析了贯通测量的主要误差源，对涉及的联系测量和地下导线测量两个重要环节进行了详细的误差公式推导、分析，提出了保证地铁顺利贯通的测量精度保证措施。通过青岛地铁某隧道贯通测量结果表明：所有精度指标符合《城市轨道交通工程测量规范》要求，取得了良好的效果。

2 贯通测量关键环节

从贯通测量的整个流程看，主要涉及地面控制测量、联系测量和地下控制测量等关键环节。由于地面控制测量、联系测量、地下控制测量及细部放样误差的影响，使得两个相向施工的贯通面，单向施工的贯通面与预留面施工中线不能理想衔接，从而产生的错开现象，即为贯通误差。而由于地面环境较好，精度较易保证，因而以下主要讨论联系测量和地下导线测量两个关键环节。

2.1 联系测量

考虑到城市地铁建设实际，联系测量一般采用竖井悬挂钢丝的一井定向。一井定向主要采用连接三角形法，如图1所示。

图1连接三角形示意图

C和C′称为井上下的连接点，A、B点为两垂球线点，从而在井上下形成以AB为公用边的三角形ABC和三角形A′B′C′。

连接测量时，在连接点C和C′处按测回法测量角度φ、φ′、γ、γ′。同时丈量井上下连接三角形的6个边长a、b、c、a′、b′、c′。

由图1可知，井下导线起始边C′D′的方位角αC′D′可用下式计算：

αC′D′=αDC+φ-α+β′+φ′±4×180°

(1)

方位角αC′D′的误差就是定向误差，以mαC′D′表示。它除了包括计算中所用到的各角度误差外，还有投向误差θ。因此，总的定向误差为：

(2)

当α≈0°，β≈180°(或α≈180°，β≈0°)时，则各测量元素对于垂球线处角度的精度影响很小。因为此时

tanα≈0，tanβ≈0，cosα≈1，cosβ≈-1

垂球线处角度误差为[2]：

(3)

2.2 地下导线测量

地下工程地下平面控制测量通常采用支导线形式。通过对测角和测距误差分析[3]可以看出，由于测角量边误差的积累，必然使导线点位位置产生偏差，从而产生贯通误差。如图2所示，1、2、3、…等导线点的点位没有误差，1′、2′、3′、 …等导线点是在测角量边误差影响下各相应导线点的位置。

图2井下支导线误差

设β1、β2、…、βn为所测导线的左角；l1、l2、…、ln为导线的边长；α1、α2、…、αn为导线边的坐标方位角；mβ1、mβ2、…、mβn为导线角度的误差；ml1、ml2、…、mln为导线边长的误差。

支导线终点K的坐标可按下式确定：

(4)

而导线边的坐标方位角是所测角的函数，即

(5)

由此可见，导线终点的坐标是整个导线所测角度和边长的函数，因而导线终点坐标的误差公式为：

(6)

上式等号右边第一项为测角误差对终点坐标的误差影响，第二项为量边误差的影响。

(7)

设Ri为导线终点与某一导线点连线长度，Ryi为Ri在y轴上的投影(如图3所示)，则：

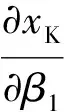
(8)

将以上各式带入(8)式可得：

(9)

式中：Rxi—导线终点与各导线点的连线长度在x轴上的投影。

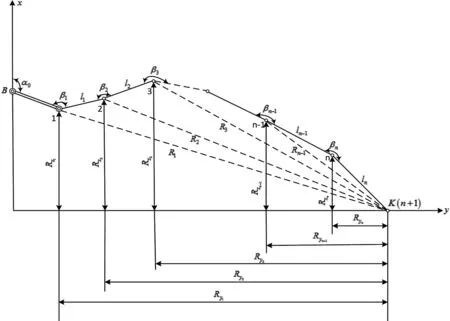
图3 Ri及其在坐标轴上的投影

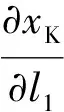
将以上各式带入式(8)可得：

(10)

当等精度测角时可得：

(11)

3 关键技术及精度指标确定

隧道贯通测量主要涉及联系测量和地下导线测量等关键环节，正确估算这两个关键环节的误差，是科学制定技术方案和保证隧道准确贯通的关键。本部分首先分析各环节指标的确定，在满足要求的前提下进行分析，并给出具体的使用建议。

3.1 井下起始方位角中误差确定

根据《城市轨道交通工程测量规范》(GB50308-2008)中规定，暗、明挖隧道和高架结构横向贯通测量中误差为 ±50 mm，高程贯通测量中误差为 ±25 mm[3]。考虑到地面控制测量精度较易满足[4]，可将误差分配如下：地面控制测量中误差 ±24 mm，联系测量中误差 ±36 mm，地下导线测量中误差 ±30 mm。地面控制测量不受地下施工条件的影响，而由式(11)可知地下控制测量点位中误差随距离的增长而增大，因而当隧道长度越长时需要的井下起始边方位角精度越高。

联系测量中误差≤36 mm可理解为联系测量坐标、方向传递对地下导线最远处点位引起的横向误差。假设隧道长度为 2 km时，由式(11)简化可求取井下起始边方位角中误差应小于±3.71″，即

(12)

式中，mα为井下起始边方位角中误差，L为地下导线长度，m2为联系测量中误差 ±36 mm。

3.2 联系测量误差分析与精度指标确定

联系测量一般采用联系三角形法，由式(2)可知，井下起始方位角中误差主要由垂球线角度误差mα、mβ′，连接角误差mφ、mφ′，井上起始边方位角mαDC以及投点误差mθ组成，假定井上起始方位角和连接角处无误差，投点误差为±2.9″[4]，则由式(2)可以求得垂球线处的连接角误差应≤±1.64″。 根据《城市轨道交通工程测量规范》(GB50308-2008)要求，在满足γ小于1°，距离测量选用I级测距精度(1 mm±1 ppm×D，D为边长，以km为单位)的仪器和反射片测距时，测距中误差ms为 1 mm，依据式(5)可计算a、c边长与角度γ测量误差之间的关系，结果如下：

边长a、c与角度γ测量误差关系 表1

由表1可见，在满足规范要求的前提下，角度γ的测角中误差应≤±1.33″，依据规范要求[4]，测角宜采用0.5″级全站仪按4个测回进行施测。

3.3 地下导线测量误差分析与精度指标确定

依据式(11)可知，边长测量误差主要与导线的形状、终点距起始点距离有关，相对来说较易控制，对地下导线横向误差影响较小；而角度测量误差源较复杂，对地下导线测量的影响较大，当地下导线敷设为近似等边直伸形支导线时，式(11)可简化为：

(13)

假设地下导线的长度为2 km、地下导线测量中误差≤±30 mm，依据式(13)可得到导线边长、测站数以及测角中误差之间的关系，如表2所示。

从表2可以看出当导线边长不超过 150 m、测站数超过14时，测角中误差应≤1.36″，依据规范[4]，测角宜采用0.5″级全站仪按4个测回进行施测、测距宜采用Ⅰ级(1 mm±1 ppm×D，D为边长，以km为单位)以上测距精度按2个测回进行施测。

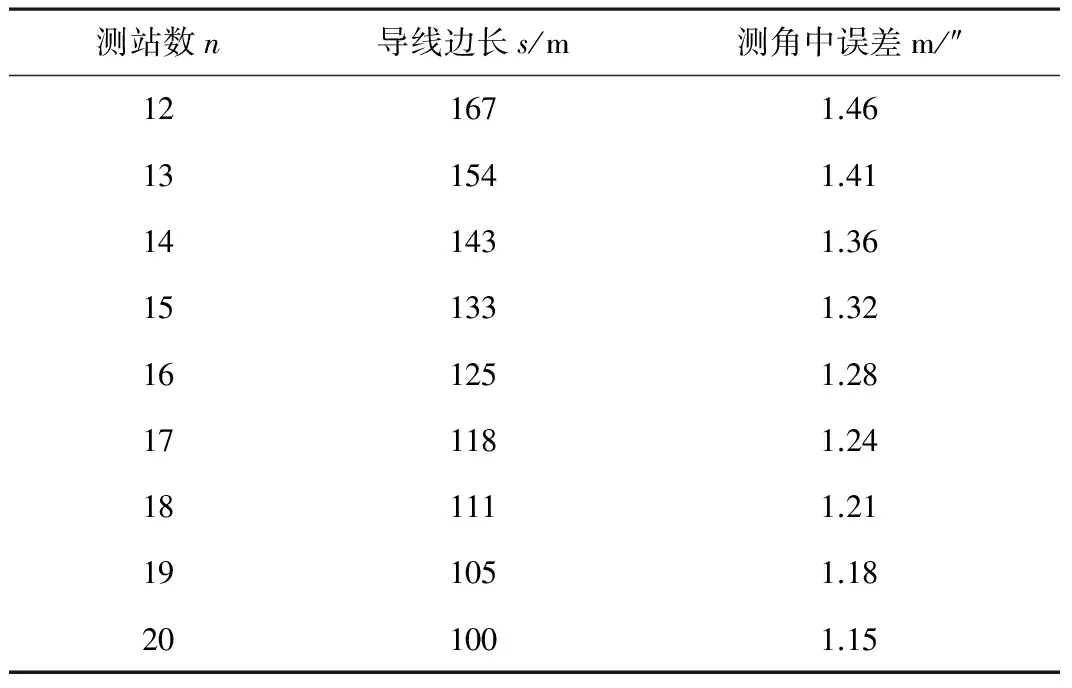
导线边长、测站数和测角中误差的关系 表2

4 工程应用与分析

青岛地铁某两个施工竖井位于市区车流密集地段，平均井深约 30 m，两井间相距约 1.5 km，施工单位分别从两竖井相向开挖，在大约两竖井中间位置贯通，开挖前在两施工竖井分别采用联系三角形法将地面坐标和方位引入地下，在整个过程中对贯通测量的关键工序进行了严格的技术方案设计，并采取了相应的满足上文分析要求的误差控制措施。为满足要求，采用徕卡TS30测量机器人(标称精度：±0.5″、0.6+1×D，D为边长，以km为单位)测量角度、距离，角度测4个测回、距离对向观测2个测回，对两竖井间进行了贯通后的相关测量工作。

本文分别从两竖井采用支导线的方式测至贯通点，然后整体联测综合平差，分析了平面和高程测量对比较差；在此基础上，结合设计对贯通测量误差进行了分析。

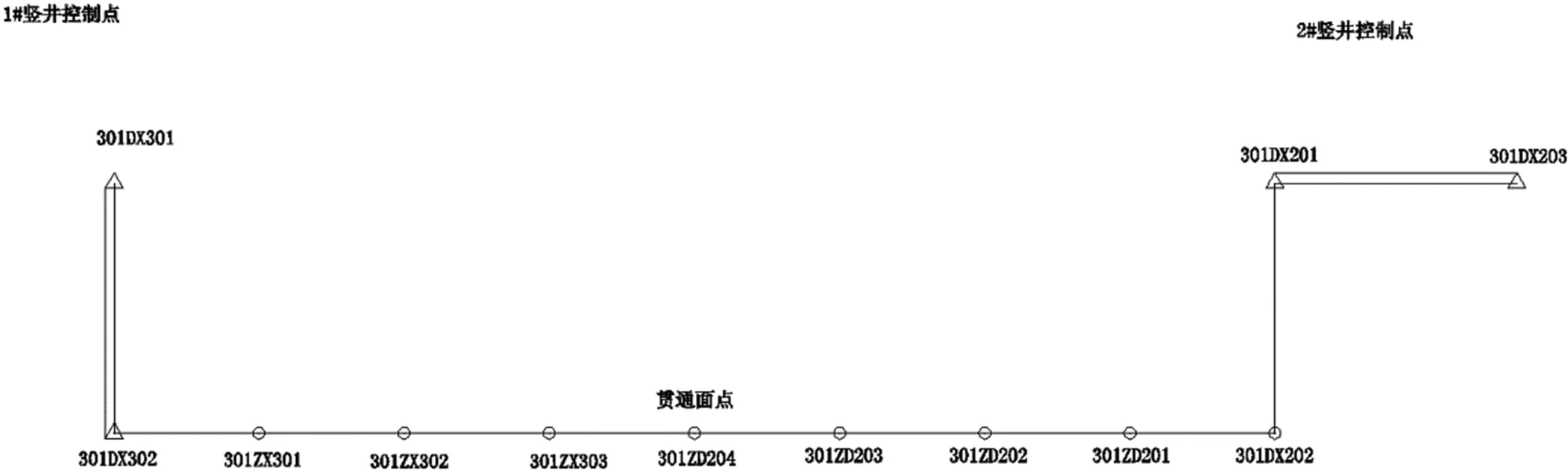
图4 竖井间贯通测量示意图

(1)平面和高程较差对比分析

平面坐标较差 表3

高程较差 表4

①从表3和表5可以看出，贯通点坐标与控制点联测坐标较差分别为 -15.3 mm、17.1 mm；②从表4可以看出，贯通点高程较差为 1.7 mm；③贯通测量结果符合《城市轨道交通工程测量规范》(GB50308-2008)限差要求。

(2)贯通误差分析

贯通点位误差 表5

①由表5可知，贯通点的x向误差为 0.94 mm，y向误差为 0.97 mm，点位误差为 1.35 mm。贯通点满足技术方案预估精度要求；②根据设计，1#竖井～2#竖井贯通点的线路方向与坐标北方向夹角为246°27′02.21″，由此计算，1#竖井～2#竖井横向贯通误差 20.9 mm，纵向贯通误差为 9.6 mm，高程贯通误差为 1.7 mm。符合《城市轨道交通工程测量规范》(GB50308-2008)限差要求。

5 结 论

贯通测量在地铁建设中至关重要，本文抓住贯通测量中的两个关键工序，结合青岛城市地铁建设实际，对联系测量和地下导线测量两个重要环节进行误差分析和精度预估，提出了适合青岛地铁自身实际的测量精度保证措施，通过实际工程验证，取得了较好的效果，从一定程度上克服了贯通测量的难点，为地铁工程顺利建设提供了良好的基础保证。

[1] 张正禄等. 工程测量学[M]. 武汉：武汉大学出版社，2002.

[2] 张国良，朱家钰，顾和和. 矿上测量学[M]. 徐州：中国矿业大学出版社，2001.

[3] 郑文华. 地下工程测量学[M]. 煤炭工业出版社，2011.

[4] GB50308-2008. 城市轨道交通工程测量规范[S].

[5] 王启善. 特长距离高精度巷道贯通测量方案设计及精度分析[J]. 煤矿安全，2011，42(3)：135-138.

[6] 程远达，傅晓明. 小半径、大深度隧道贯通测量的研究和实践[J]. 城市勘测，2014(2)：134-137.

[7] 高绍伟. 激光铅垂仪向上投点在地铁隧道工程中进行联测测量的实践[J]. 北京测绘，2008(2)：57-60.

[8] 刘建伟，师军良. 一井定向在地铁隧道中的应用[J]. 内江科技，2009(6)：7-12.

ErrorAnalysisandApplicationResearchontheTransfixionMeasurementofSubwayTunnel

Hu Yuxiang，Zhang Hongde，Wang Zhi，Sun Xiaoli
(Qingdao Geotechnical Investigation and Surveying Institute，Qingdao 266032，China)

The shaft piercing measurement is the key and difficult point in the subway tunnel construction，and exploring the essential measures through suitable for city subway engineering is important，according to the basic process of tunnel measurement，based on the analysis of the main error sources through measurement，this paper implies error analysis and accuracy prediction on measurement of contact and underground traverse and proposes measurement accuracy for Qingdao Metro actual measures. Good results are achieved through practical engineering.

the shaft piercing measurement；error analysis；accuracy prediction；contact measurement；underground traverse survey；Qingdao Metro

1672-8262(2017)06-126-05

P207

B

2017—03—02

胡玉祥(1988—)，男，硕士，工程师，主要从事GNSS数据处理与应用、城市轨道交通测量研究工作。