收获方法 融汇知识——一道简单几何题的探究与思考

□胡连成

（丰县华山初级中学，江苏丰县 221700）

收获方法 融汇知识
——一道简单几何题的探究与思考

□胡连成

（丰县华山初级中学，江苏丰县 221700）

比知识重要的是方法，比方法重要的是兴趣.在数学解题教学中教师应该引导学生主动参与，通过一题多解，对习题的解法进行探究，实现学生对问题的多维思考，对知识的融会贯通，使学生收获的不仅是解决问题的方法，更是探究意识的培养、学习兴趣的激发.

解法探究；一题多解；知识融合；兴趣培养

一、题目介绍

二、探索过程

生1：太简单了，已知AF⊥DE，那么不就说明CF⊥DE了吗？

师：请同学们仔细阅读题目，你认为点A，F，C在同一条直线上吗？

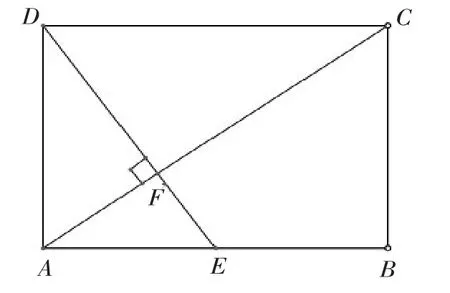
图1

生1：根据图形可以看出点A，F，C都在矩形ABCD的对角线上呀！

生2：已知条件中没有说线段AF，CF在矩形ABCD的对角线上，也就是说“点A，F，C在同一条直线上”是未定的结论，需要我们证明.

至此同学们恍然大悟，问题没有那么简单，大家陷入思考之中……

生3：要证CF⊥DE，通常需要证明∠DFC=90°，因此我想到通过计算证明“DF2+CF2=CD2”成立来说明△DFC是直角三角形.

师：这位同学执果索因的逆向思维方式给了我们一些启示，谁能帮助他计算CF的长呢？

生4：生3的解法给我一些启示，我想过F点作FG⊥DC（见图2），得到Rt△FDG和Rt△FCG.

根据 CD∥AB，可得∠CDF=∠DEA，又知∠DGF=∠EAD=90°，所以△DGF∽△EAD，可求，所以CG=CD-DG=2-故可得.所以△DFC为直角三角形，即CF⊥DE.

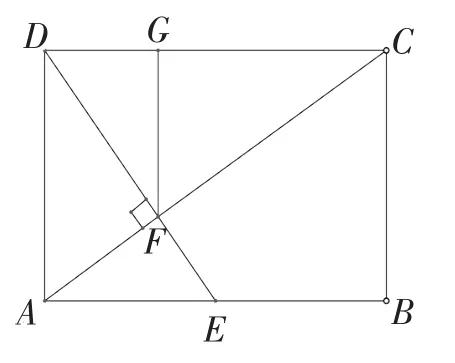
图2

师：生4通过F点作FG⊥DC构建Rt△FDG和Rt△FCG，使“需证”和“条件”建立联系.连续运用勾股定理巧妙地证明了“DF2+CF2=CD2”，太棒了！同学们还有什么发现吗？

生5：我感觉生4的证法过于复杂，我想如果充分运用相似三角形可有更简洁的方法.借鉴前面同学的结论可知.所以，所以根据CD∥AB可得∠CDF=∠DEA.所以△DFC∽△EAD ，所以∠CFD=∠DAE=90°，亦可证CF⊥DE.

师：图形中蕴含了丰富的知识，同学们不但要认真审题，同样也要认真审图，这位同学通过“审图”充分挖掘图形中的相似三角形，发现较为简便的证明方法，这种好习惯值得我们借鉴.

生6：我的证明思路和前几位同学的不同，既然本题的难点是已知条件没有说明点A，F，C的三点共线，我想能否过点C作CF′⊥DE，垂足为点F′（见图3），然后说明F′和F是同一点呢？我们在学习“三边成比例的两三角形相似”时曾经运用过类似的方法解决问题，于是我就想能否借鉴教材中的方法呢？

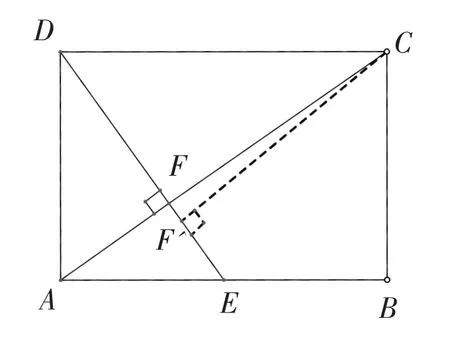
图3

证明过程如下：过点C作CF′⊥DE，垂足为点F′.

根据∠CDF′=∠DEA，∠CF′D=∠DAE，可证△CF′D∽△DAE.根据可求DF′=，根据生3解法可知所以DF′=DF，即点F′与点F重合，所以 CF⊥DE.

师：生6的解法太精妙了，由因导果或执果索因的常规思考有难度时，换个角度思考问题，通过构造CF′⊥DE，利用相似证明了DF′=DF，从而说明F′与F是同一点，这种方法我们称为同一法.这位同学善于精读教材，在反复品味中思考问题，归纳方法，这种好习惯值得我们学习.

生7：生6的解法给我很大的启发，我们在学习一次函数时常有判断三点共线的问题.于是我想到一种新的解题方法：以点A为坐标原点、AB所在的直线为x轴、AD所在的直线为y轴建立平面直角坐标系（见图4）.设直线AF的解析式为y=kx，根据k=tan∠FAE=tan∠ADE可得，当x=2时所以可以判断在直线y=上，即A，F，C三点共线，所以CF⊥DE.

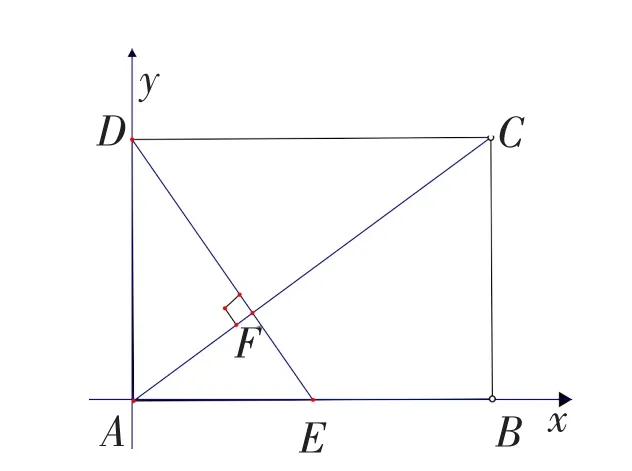
图4

师：这位同学给我们展现了更为“惊艳”的解法，运用一次函数和锐角三角函数知识说明了 A，F，C三 点 共 线.你 是 如 何 想 到“k=tan∠FAE”的呢？

生7：一开始我想用待定系数法求直线AC的函数表达式，但我发现F点坐标不好求，我在学习“锐角三角函数”时，发现一次函数y=kx+b的一次项系数“|k|”的大小和直线的“倾斜程度”有关，而三角函数中坡度i=tanα也和直线的“倾斜程度”有关，二者之间必有某种联系，我通过结合实例进行归纳，并查阅相关资料，发现i=tanα=|k|是成立的.

此时，全班同学对此赞不绝口，笔者也是为之一振，数学学习的目的不就是通过探索活动发现数学规律，并运用规律解决问题的吗？

生8：看到生7运用三角函数的过程，我想到另一种解法，连接AC，因为.所以tan∠FAE=tan∠BAC.所以∠FAE=∠BAC.故AF与AC重合，所以CF⊥DE.

至此，全班自发响起阵阵掌声，大家不由得赞叹解法的精妙.大道至简，一道习题5种解法，从不同角度思考问题，由繁至简、数形结合、规律运用、知识交融……令人拍案叫绝.

三、几点启发

（一）知识学习，重视生成过程

知识学习是个体经历探索、碰撞、发现、感悟的过程，学生在知识生成的探索中收获的不仅是知识，更重要的是方法经验和情绪体验，这是个体不断成长的重要过程.“一个定义、几项注意、反复练习”的灌输式学习方式，忽视了学生探索知识的过程，不利于学生的思维发展和心理成长，早已被我们所抛弃.俗话说“磨刀不误砍柴工”，虽然知识探索时效不高，课本知识可能会遗忘，但探索知识收获的经验、方法、思想却将伴随学生一生，使他们终身受益.本例探索中，学生由课本知识的探索收获想到用同一法解决问题，给人以“惊艳”之感.再比如，我们学习“圆周角的度数等于它所对弧上的圆心角度数的一半，同弧或等弧所对的圆周角相等”时，应该留足够时间经历知识的探索过程，从中体会“分类讨论”“从特殊到一般的思考方法，一般问题转化为特殊情况的解决方法”等相关的思想.教学中花费时间经历知识“再生成”过程，短期效果可能不明显，但从长远来看，一定会有助于学生的思维发展，正所谓“无心”插柳柳成荫，“不经意间”的知识探索生成会使学生有意想不到的收获.因此，数学教学应重视知识探究学习，通过思考、交流、感悟，经历知识的“生成”过程，在主动知识探索中体会数学的思想方法，感悟探索的快乐.

（二）问题思考，善于探究规律

数学教学应重视问题探索，鲜活的具体问题是数学知识的载体，数学知识是问题的灵魂.学习数学从某种角度来说就是通过探索问题发现数学知识的内在规律，并运用规律解决问题的过程，规律可能是计算方法和技巧，可能是解决问题的思路和途径，可能是抽象的数学思想与方法……对于具体的问题思考，不要局限于解决问题，应进一步追问与探索，问题解决的方法是否具有普遍性、规律性，问题的结论是否可以进一步推广延伸，与其他内容是否具有内在的联系，数学问题是具体的、可变的，数学知识规律是简洁而恒定的.例如，本例中，学生根据一次函数图象的“直线倾斜”和锐角三角函数“边的倾斜”，思考其内在联系，归纳了“i=tanα=|k|”，岂不精妙！再比如，我们学习了二次函数的平移规律“上加下减、左加右减”，那么回头再思考八年级学习的一次函数和反比例函数是否也有类似的平移规律呢？再如，我们学习了“菱形的面积等于对角线乘积的一半”，那么，结论的背后蕴含的是“只要四边形对角线互相垂直，它的面积就等于对角线乘积的一半”的规律，学生在学习了“锐角三角函数”后，可以进一步探索“四边形的面积和两条对角线长度及对角线的夹角锐角 α 有 内 在 普 遍 规 律”.如果教学中有意识地培养数学的这种规律探究意识，学生的数学素养一定会有极大的提高.

（三）知识运用，重视融会贯通

知识的学习，妙在通透.“通”为互通，知识点融会贯通、四通八达、形成体系；“透”指透明，知识点本质要义一目了然、熟烂于胸.数学教学要处理好知识融合的问题，形成完整的知识结构，实现“既见树木又见森林”的知识整合目的.本例中解法的探究历程，不单纯以解答问题为目的，而应从多种解法中对比、联系，一题多解实现对问题的多维思考，多解归一实现知识的融会贯通.例如，本例中，一次函数图象的“直线倾斜”和锐角三角函数“边的倾斜”内容融合统一.再如，方程、不等式与函数的融合统一；三角形“内心、外心、重心及正三角形的中心”的联系；平行四边形、矩形、菱形、正方形的图形性质和证明方法的联系和区别；统计中的“频率”与“概率”的内在统一等.

（四）课堂教学，重在激发兴趣

课堂的有效性取决于学生主动参与度，调动学生主动性需要培养学生对知识探索的强烈兴趣.比知识更重要的是方法，比方法更重要的是兴趣，学习兴趣是课堂焕发生命活力的前提.学习兴趣的培养需要教师精心设计问题引领探索活动，问题的选择设计外表要鲜活——有趣，能吸引学生的眼球；里子有内涵——方法、思想蕴含其中.问题的引导要把握时机，在“好雨知时节，当春乃发生”处引导，于“随风潜入夜，润物细无声”时熏陶.在浓厚的求知欲和好奇心的引领下，激情思维才能碰撞出火花，才能形成“百花齐放、百家争鸣”的良性课堂互动氛围.本例在问题的探索中，学生收获的不仅是问题解决的不同策略，更重要的是激发了数学探究的兴趣、感受了探索的乐趣，让学生感到数学好玩、有趣，这才是数学教育的最高艺术 .