电磁轨道发射装置轨道几何参数对电流分布的影响
贺景瑞,李小将,齐 跃
( 航天工程大学 a.研究生管理大队; b.航天装备系, 北京 101416)
【航天工程】
电磁轨道发射装置轨道几何参数对电流分布的影响
贺景瑞a,李小将b,齐 跃a
( 航天工程大学 a.研究生管理大队; b.航天装备系, 北京 101416)
为分析电磁轨道发射装置的轨道几何参数对轨道电流分布的影响,采用有限元仿真软件COMSOL Multiphysics,研究轨道宽度、高度、宽高比与轨道最大电流密度的关系,仿真计算矩形、凸形和凹形3种不同截面的轨道电流分布。结果表明:增加轨道宽度和高度,轨道电流密度降低;在截面积不变条件下,减小轨道的宽高比,轨道电流密度降低;在矩形、凸形和凹形截面轨道中,凸形截面轨道在电流上升沿阶段具有最均匀的电流分布。
电磁发射;电流分布;轨道参数;有限元分析
电磁轨道发射装置是一种新型发射装置,发射时电流通过轨道和电枢之间的闭合回路产生磁场,电枢在磁场作用下产生电磁力将物体沿轨道加速至超高速。电磁轨道发射装置因其具有发射初速高、成本低、速度容易控制等优点,在超高速撞击实验、微小卫星发射、防空反导等方面具有广阔的应用前景。
电磁轨道发射装置上的电流分布情况是决定发射装置效率和寿命的重要因素。轨道的形状、尺寸、材料等参数能够影响电流在轨道上的分布情况[1-2]。近年来,国内外学者针对电磁轨道发射装置的电流分布情况展开了大量的研究。文献[3]建立二维矩形轨道模型,使用有限元的方法分析轨道长度、宽度、高度变化对电流分布的影响,但其对照仿真实验数目较少。文献[4]采用二维边界元方法对矩形截面和弧形截面轨道几何参数和电流分布的关系进行了研究,但其未考虑电枢的存在,并且未计算轨道内部的电流分布。文献[5]建立了轨道和电枢模型,仿真计算了二维轨道上的电流分布,但其仿真结果未体现出趋肤效应对电流分布的影响。文献[6]利用智能估算方法(IEM)导出了矩形轨道截面和凹弧形轨道截面的电流分布,但其没有计算凸弧形轨道截面的电流分布。文献[7]采用有限元软件MAXWELL的瞬态场求解器对矩形、凸形和凹形3种不同截面轨道进行电流分布的数值仿真,但未分析驱动电流下降沿的轨道电流分布情况。文献[8]采用Ansoft12有限元软件对比仿真分析了矩形、跑道形、圆形三种不同截面的轨道,未分析凸形和凹形截面轨道的电流分布。文献[9-10,]在时域谐波下仿真了电磁轨道发射装置的二维和三维电流分布,但未仿真一次发射中不同时刻轨道内的电流。
在本文中,考虑电枢存在的影响,采用COMSOL Multiphysics有限元仿真软件,建立不同轨道参数的电磁轨道发射装置模型,采用瞬态求解器从中直接求解轨道的电流分布进行分析。选择铜作为轨道材料,在静止条件下,分析在驱动电流不同时刻的轨道内电流分布情况。选择电磁轨道发射装置设计时可能采用的矩形、凸形和凹形三种截面,分别建立模型求解其电流分布。通过改变轨道宽度、高度和宽高比,研究其与轨道电流密度的关系。通过分析仿真结果,为电磁轨道发射装置的优化设计提供参考。
1 不同时刻轨道中的电流分布
电磁轨道发射装置的驱动电流是脉冲电流。在发射过程中,通过轨道的电流从零迅速增大,经过平沿阶段然后减小,在电枢与轨道分离时减小至零[11]。图1所示为本文使用的驱动电流波形,幅值为1 kA,上升沿时间0.8 ms,平沿时间1.2 ms,下降沿时间3 ms。
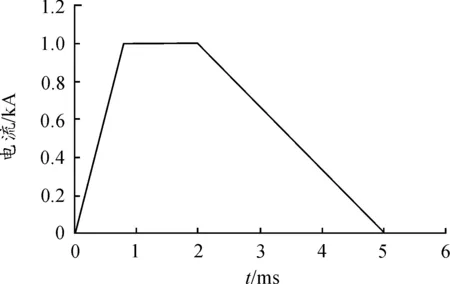
图1 驱动电流波形
在脉冲电流的上升沿、平沿和下降沿,电磁轨道发射装置内的电流分布有显著的差别。了解轨道内的电流分布是电磁轨道发射装置优化设计的基础。因此,有必要对轨道内不同时刻的电流分布状况进行分析。
建立轨道的3D模型,利用有限元仿真软件COMSOL Multiphysics对轨道内的电流分布进行仿真。轨道选择具有一般性的矩形截面轨道,轨道长50 mm,宽10 mm,高20 mm,采用铜作为轨道材料。加载幅值为1 kA的驱动电流后,轨道在0.1 ms,0.4 ms,1.4 ms,3.4 ms时刻的电流密度云图如图2所示。
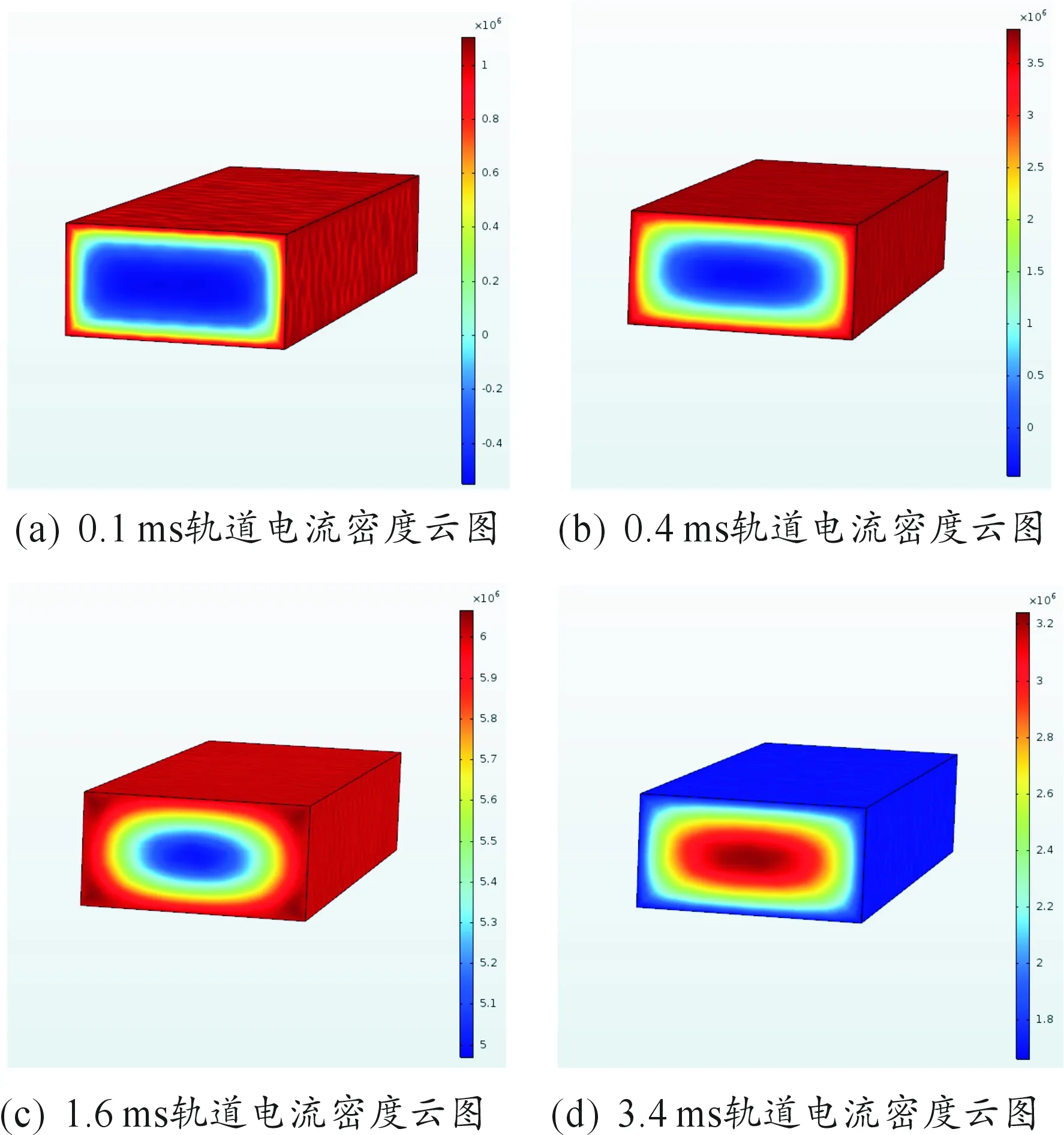
图2 不同时刻轨道电流密度云图
图2(a)和(b)中驱动电流处于上阶段,变化的电流在轨道内产生趋肤效应,电流趋向于在轨道四周表面流动。图2中驱动电流从轨道左端流入,右端流出,但并不是所有时刻电流密度矢量的方向都由左指向右,图2(a)的深蓝色位置,电流密度的沿轨道方向分量Jx=-5.41×105A/m2,相对应的在轨道表面Jx=1.06×106A/m2。轨道在0.1ms时的电流密度矢量如图3所示。

图3 0.1 ms时刻电流密度矢量图
图3中,在轨道表面电流密度矢量(红色)的方向与驱动电流方向相同,由轨道左端指向右端。而轨道内部电流密度矢量(蓝色)方向与轨道表面电流密度矢量方向与轨道表面相反。这种现象是驱动电流迅速上升引起的涡流现象导致的。
图2(b)中电流密度仍集中在轨道的表面区域,实际上在整个驱动电流上升沿阶段,轨道上的趋肤效应一直较为明显。这造成了能量传输的损耗和轨道局部位置温度过高进而引起轨道损伤的情况。图2(c)中,1.6 ms时刻驱动电流处于平沿,电流的趋肤深度加深,虽然趋肤效应仍存在,但是已经十分微弱,轨道内部与表面的电流密度接近。在图2(d)中电流处于下降沿阶段,轨道的趋肤效应消失,轨道中的电流分布与电流的上升阶段相反,电流集中在轨道内部,受轨道内涡流的影响,轨道表面部分区域电流反向。
2 不同轨道结构参数下轨道电流分布特性
为了解轨道结构对电流分布的影响,下面针对几种不同形状的轨道分析其轨道结构参数与电流分布的关系,为电磁轨道发射装置设计提供参考。
2.1 矩形截面轨道电流密度分布
对于矩形截面轨道,分析轨道高度H、轨道宽度W以及在截面积S不变的条件下轨道宽高比W/H对轨道电流分布的影响。在矩形截面轨道的研究中,轨道的基本参数为:宽度10 mm,高度20 mm,长度50 mm,间距15 mm。图4为0.4 ms时和1.4 ms时矩形截面轨道电流密度分布云图。
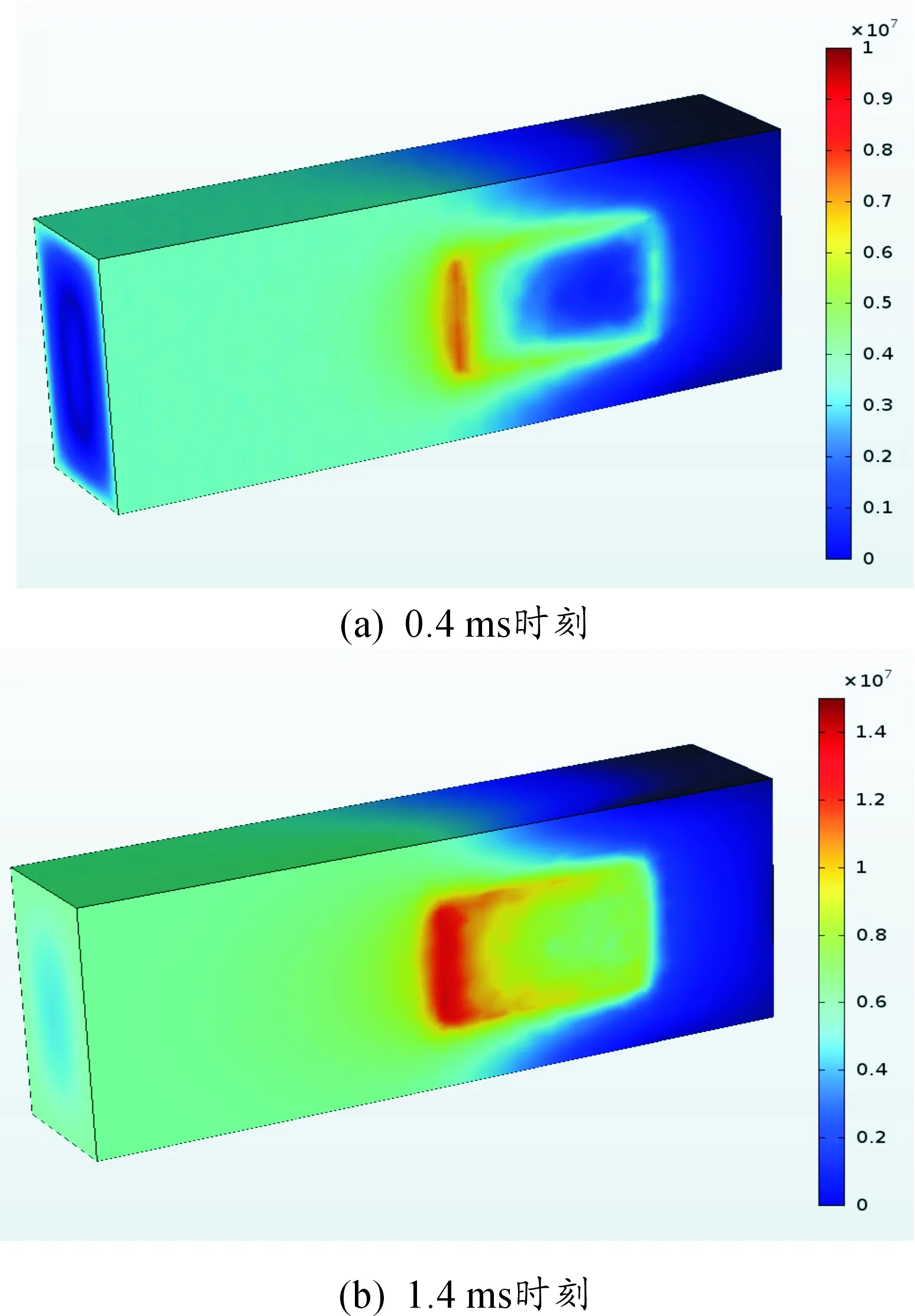
图4 矩形截面轨道电流分布
在图4所示的矩形截面轨道电流密度分布云图中,电流聚集在枢轨接触面后部及其两侧。在0.4ms时刻,趋肤效应引起电流密度由外至内逐渐递减,在轨道中心形成反向电流。在枢轨接触面的中前部,形成了低电流密度区域,整个接触面的电流分布不均匀。在1.4 ms时,轨道上趋肤效应减弱,最大电流密度虽然仍出现在枢轨接触面尾部,但整体电流分布更加均匀。
通过调整轨道的宽度、高度、宽高比3个参数,分析轨道参数对电流分布的影响,具体参数选择如表1。
当弹体的侵彻速度u大于临界速度uf0时,弹靶附近的材料会产生极大的静水压,因此可以忽略靶体材料的剪应力,此时弹靶界面材料可以看成近似流体(此为A-T模型的基本假设)。基于文献[19,20-21,25]的研究,本文认为长杆弹侵彻混凝土靶体时,靶体的响应区与金属靶板的响应区类似,同样可以划分为流动区、塑性区(包括破碎区和开裂区)和弹性区。图1为长杆弹侵彻半无限混凝土靶示意图。

表1 轨道参数
轨道最大电流密度计算结果如图5所示。
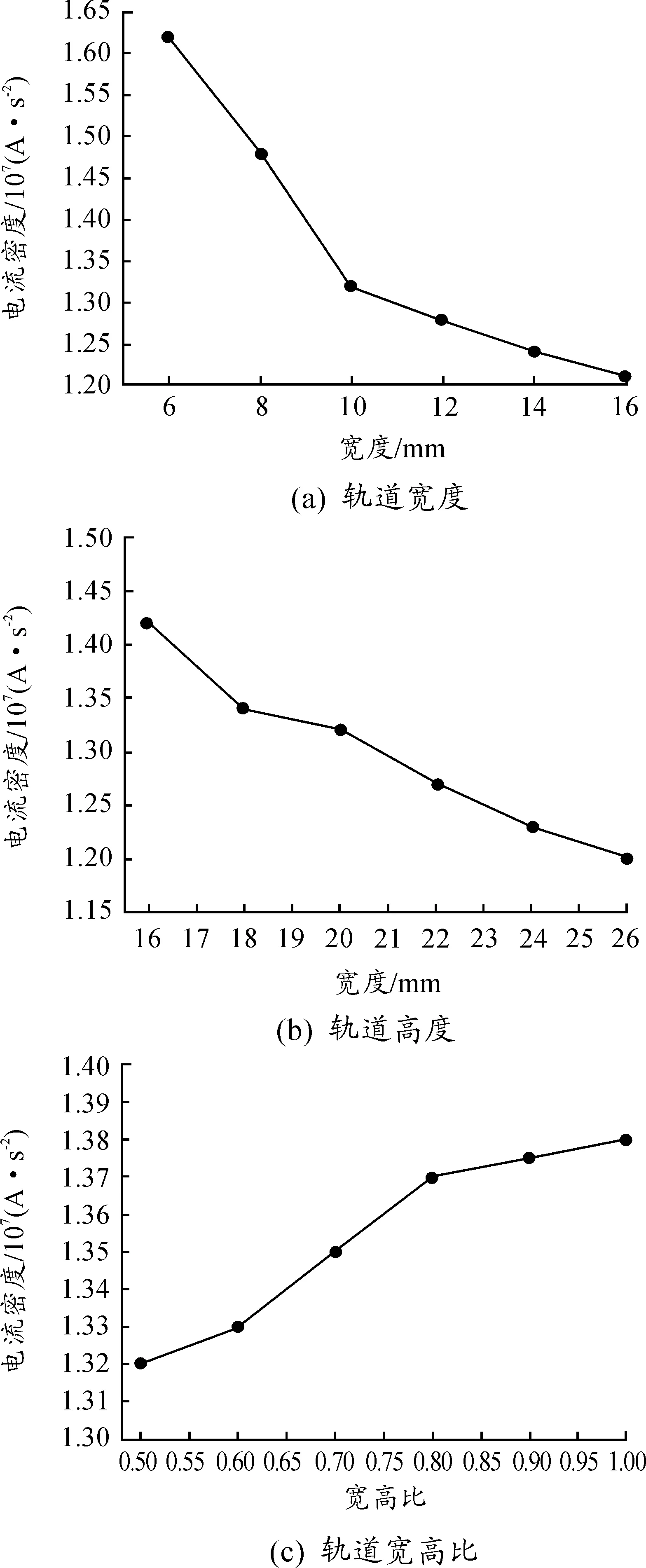
图5 各轨道参数与电流密度关系曲线
图5(a)中,横坐标表示轨道宽度,纵坐标表示轨道在1.2 ms时的最大电流密度。在轨道宽度小于10 mm时轨道,随着轨道宽度增大,轨道电流密度迅速下降。当轨道宽度大于10 mm时,随着宽度的增加,电流密度下降速度趋缓。这提示电流密度的降低不仅仅是轨道通流截面积增大引起的。考虑到高频驱动电流的趋肤效应,计算其趋肤深度。铜轨道趋肤深度计算公式为:
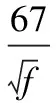
(2)
式中:f为驱动电流频率;d为趋肤深度,驱动电流频率为200 Hz,计算得驱动电流趋肤深度为4.73 mm。因此,当轨道宽度小于电流在上下表面的趋肤深度,即W<2×4.73=9.46 mm时,轨道内部没有低电流密度区,轨道宽度增加能够有效降低轨道内部电流密度;当轨道宽度W>9.46 mm时,电流主要分布在轨道边沿至深度4.73 mm区域内,增加宽度对电流密度的影响变小。
在图5(b)中,增加轨道高度,轨道上的电流密度逐渐变小。因为此时轨道宽度和轨道高度均大于9.46mm,所以此时轨道高度的增加实际上是通过增大通流面积降低轨道电流密度。
从图5(c)中可知,矩形轨道截面积不变的条件下,随着轨道宽高比的不断增加,轨道上的最大电流密度升高。这是因为在短时间、大电流条件下,轨道内的趋肤效应十分明显。电流主要集中分布在轨道的外表面上,流经轨道内部的电流较少甚至方向相反,由内向外呈现出逐渐升高的梯度分布。保持轨道长度不变和轨道截面面积不变,减小轨道宽度和高度的比值,使轨道更加扁平,能够有效消除趋肤效应引起的低电流密度区域。因此,通过减小轨道的宽高比,使得轨道上的电流分布更加均匀,电流密度也大幅下降。
2.2 弧形截面轨道电流密度分布
弧形截面轨道分为凸形截面轨道和凹形截面轨道两类。凸形截面轨道的基本参数为:宽度9 mm,高度20 mm,弧高3 mm。凹形截面轨道的基本参数为:宽度11 mm,高度 20 mm,弧深3 mm。凸形截面轨道和凹形截面轨道在0.4 ms时刻和1.4 ms时刻的电流密度分布如图6和图7所示。
由表2可以看出,轨道截面形状对接触面最大和最小电流密度的影响主要发生在处于驱动电流上升沿的0.4 ms时刻,处于驱动电流平沿的1.4 ms时刻,轨道截面形状对接触面最大和最小电流密度的影响不再明显。
0.4 ms时刻凸形截面轨道具有最大的电流密度,凹形截面轨道的最大电流密度略高于矩形轨道。从图6中可以看出,凹形截面轨道的枢轨接触面中前部出现了深蓝色区域,这表明轨道上电流分布极不均匀,在此区域中电流密度仅为4.7×105A/m2,仅为最大电流密度的十六分之一。凸形截面轨道的接触面没有出现电流密度极低的深蓝色区域,在三种轨道中凸形截面轨道接触面的电流分布最为均匀。
1.4 ms时刻驱动电流处于平沿阶段,虽然此时凸形截面轨道的最大电流密度仍为最大,但是三种不同截面轨道的电流密度已经较为接近。在图6(b)中,凸形截面轨道的电流分布在枢轨接触面的尾部更为集中,形成了一条深红色的高电流密度带。因为通过电枢的磁场由尾部到头部逐渐降低,所以大电流集中通过电枢尾部有利于获得更高的电磁力,缺点是当集中在电枢尾部的欧姆热过高时容易引起轨道损伤。
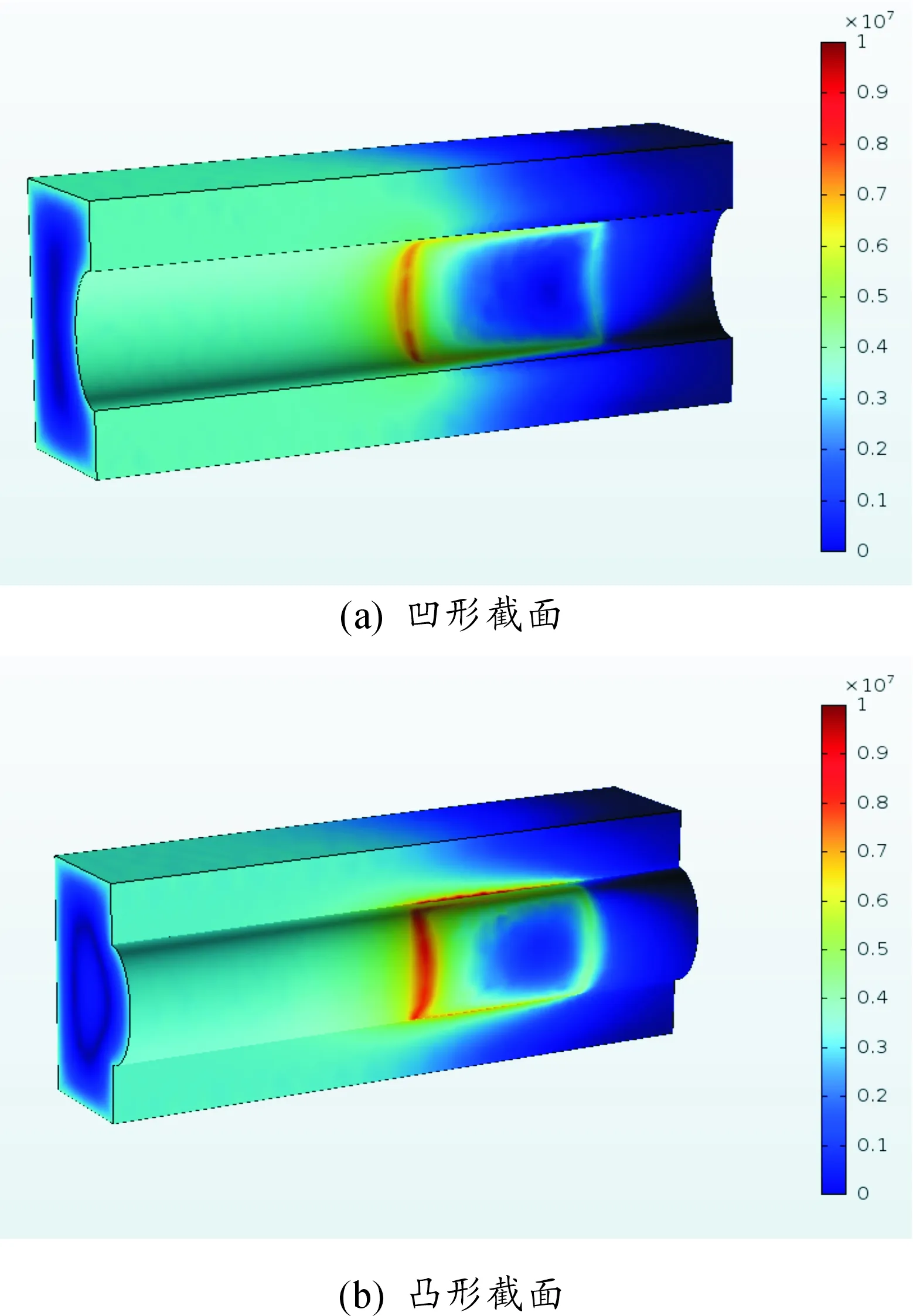
图6 0.4 ms弧形截面轨道电流分布

图7 1.4 ms弧形截面轨道电流分布
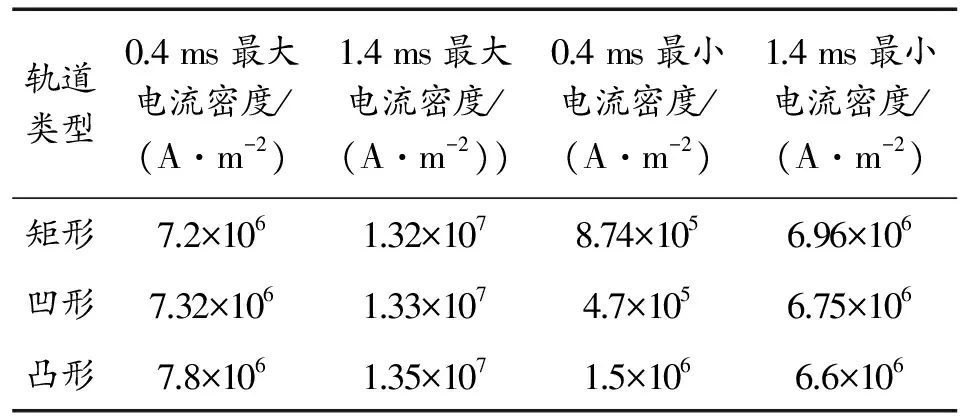
轨道类型0.4ms最大电流密度/(A·m-2)1.4ms最大电流密度/(A·m-2))0.4ms最小电流密度/(A·m-2)1.4ms最小电流密度/(A·m-2)矩形7.2×1061.32×1078.74×1056.96×106凹形7.32×1061.33×1074.7×1056.75×106凸形7.8×1061.35×1071.5×1066.6×106
凹形截面轨道边沿的电流密度高于平面形截面和凸形截面轨道。在凸形截面轨道上,中间凸起部分的电流密度较凹形截面和平面形截面更大。在三种不同截面轨道上,枢轨接触面的尾部及其两侧都具有较高的电流密度。
3 结论
本文利用COMSOL Multiphysics有限元仿真软件分析了电磁轨道发射装置在驱动电流不同时间阶段的轨道电流分布和不同轨道结构参数对电流分布的影响,为电磁轨道发射装置的实验设计提供参考,主要结论如下:
1) 轨道内的电流分布在驱动电流的不同时间阶段有明显的区别。在驱动电流上升沿,轨道内趋肤效应明显,电流集中在轨道的表面。在驱动电流平沿,轨道内电流分布渐趋均匀。在驱动电流下降沿,轨道内电流密度由内至外逐渐降低。
2) 增加轨道的宽度、高度和减小轨道宽高比均能降低轨道内的电流密度。在选择轨道结构参数时考虑驱动电流趋肤深度的影响能够更有效改善轨道上的电流分布。
3) 矩形、凸形、凹形截面轨道在枢轨接触面尾部均会出现电流聚集现象。在驱动电流上升阶段,矩形和凹形截面轨道枢轨接触面均存在电流密度极低的深蓝色区域,凸形截面枢轨接触面的电流分布较为均匀。采用凸形截面轨道有利于抑制电流上升阶段产生的损伤。在驱动电流的平沿阶段,凸形截面轨道具有最高的电流密度。
[1] KESHTKAR A, BAYATI S.Effect of Rail’s Material on Railgun Inductance Gradient and Losses[C]//Electromagnetic Launch Technology, 2008, Symposium on.IEEE, 2008:1-4.
[2] BAYATI M S, KESHTKAR A.Transition Study of Current Distribution and Maximum Current Density in Railgun by 3-D FEM-IEM[J].Plasma Science IEEE Transactions on, 2011, 39(1):13-17.
[3] KESHTKAR A.Effect of rail dimension on current distribution and inductance gradient[J].Magnetics IEEE Transactions on, 2005, 41(1):383-386.
[4] 张豪, 谢龙, 高俊杰,等.电磁轨道炮轨道形状对电流分布的影响[J].火炮发射与控制学报, 2016, 37(4):48-53.
[5] YUAN W, YAN P.Comparison of Railguns through Numerical Simulations[J].Symposium on Electromagnetic Launch Technology, 2008:1-3.
[6] BAYATI M S, KESHTKAR A,Transition Study of Current Distribution and Maximum Current Density in Railgun by 3-D FEM-IEM[J].Plasma Science IEEE Transactions on, 2011, 39(1):13-17.
[7] 李鹤, 李治源, 雷彬,等.电磁轨道炮不同截面轨道的特性分析[J].火力与指挥控制, 2014(4):45-48.
[8] 解世山, 吕庆敖, 郭春龙,等.静止条件下轨道炮电流分布特征仿真[J].火炮发射与控制学报, 2012(2):9-12.
[9] LIEBFRIED O, SCHNEIDER M, STANKEVI T, et al.Velocity-Induced Current Profiles Inside the Rails of an Electric Launcher[J].IEEE Transactions on Plasma Science, 2012, 41(5):1520-1525.
[10] STANKEVI T, SCHNEIDER M, BALEVIIUS S.Magnetic Diffusion Inside the Rails of an Electromagnetic Launcher: Experimental and Numerical Studies[J].IEEE Transactions on Plasma Science, 2013, 41(10):2790-2795.
[11] 袁建生, 李军, 左鹏,等.不同截面形状轨道的电磁炮电流分布特性分析[C]//2011中国电工技术学会学术年会.2011.
EffectofGeometricalParametersChangeonCurrentDistributionintheElectromagneticLauncher
HE Jingruia, LI Xiaojiangb, QI Yuea
(a.Department of Graduate Management; b.Department of Space Equipment, Aerospace Engineering University, Beijing 101416, China)
Current distribution in electromagnetic Launcher structure is the effective factor that determines its efficiency and life. In order to analyze the influence of rail geometrical parameters on the current distribution of electromagnetic launcher, the finite element simulation software COMSOL Multiphysics is used to study the relationship between rail width, height and aspect ratio and its current distribution. The rail current distribution in rectangular, convex and concave cross-section is simulated. The results show that increasing the rail’s width and height can reduce the rail current density. Under the condition of constant cross-section, reducing the aspect ratio of the rail can effectively reduce the rail current density. The convex cross-section rail has the most uniform current distribution at the rising edge of the driving current in the rectangular, convex and concave cross-section rail.
electromagnetic launcher; current distribution; geometrical parameters of the rail; finite element analysis
2017-09-15;
2017-10-12
贺景瑞(1992—),男,硕士,主要从事电磁轨道发射技术研究。
10.11809/scbgxb2017.12.042
本文引用格式:贺景瑞,李小将,齐跃.电磁轨道发射装置轨道几何参数对电流分布的影响[J].兵器装备工程学报,2017(12):186-190.
formatHE Jingrui, LI Xiaojiang,QI Yue.Effect of Geometrical Parameters Change on Current Distribution in the Electromagnetic Launcher[J].Journal of Ordnance Equipment Engineering,2017(12):186-190.
TJ303
A
2096-2304(2017)12-0186-05
(责任编辑杨继森)

