一种基于后悔理论的启发式医学决策曲线分析方法
王 凯,刘玉文,2,徐济成
(1.蚌埠医学院 卫生管理系,安徽 蚌埠 233030;2.中国科学技术大学 计算机科学与技术学院,安徽 合肥 230027;3.安徽农业大学 信息与计算机学院,安徽 合肥 230027)
一种基于后悔理论的启发式医学决策曲线分析方法
王 凯1,刘玉文1,2,徐济成3
(1.蚌埠医学院 卫生管理系,安徽 蚌埠 233030;2.中国科学技术大学 计算机科学与技术学院,安徽 合肥 230027;3.安徽农业大学 信息与计算机学院,安徽 合肥 230027)
决策曲线分析(decision curve analysis,DCA)已被广泛用于诊断或评价预测模型.然而,DCA的核心是基于期望效用理论的,通常受直觉系统和分析与审议双认知系统的影响,决策准确度不高.为提高预测模型的准确性,提出了一种双重模拟量表,通过预期后悔差异算子描述遗憾决策函数模型,基于经典决策树模型描述决策方案,然后对策略候选集计算净预期后悔差异值,构建决策阈值概率关系,以疾病概率的形式确定潜在错误决策的阈值,以提高模型的容错能力.实验表明,本模型具有较高的稳定性与准确性.
后悔理论;决策曲线分析;双重模拟量表;阈值概率
为消除临床决策模型的不确定性,相关专家学者提出了许多方法,主要基于统计概率模型、信息理论、模糊逻辑及熵理论等方法.文献[1]区别对待离散型和连续型属性值,基于决策链方式处理离散属性间的传递相关性,利用连续多标记决策系统扩展了传统粗糙集模型.文献[2]对Partin表的预测作用进行了评估,通过建立不同预测模型的效益模型,评估并预测了基于决策曲线分析理论的数学模型,优化了决策理论.文献[3]运用效用分析函数模拟建立了社交网络模型,估计效用函数参数,校准蒙特卡罗参数.文献[4]针对语言集数据构建云模型生成算法,采用数值模拟方法处理语言数据的基本运算,生成多准则决策模型.文献[5]针对双边匹配决策问题, 基于变步长求解模型,计算最优匹配决策方案.文献[6]以多属性决策分析中常优劣解距离法为核心构建最优云服务决策函数,获取了云模型决策最优集合.以上模型与方法虽然能够有效降低决策系统的数据噪声问题,过滤出有效的评价数据,但由于未考虑决策认知模型的主观偏好性,整体决策精准度不高.
在临床医学研究中,面向诊断及治疗的决策支持系统已在智能诊疗领域广泛应用,如慢性炎症的诊疗、传染病和肝外科的确诊等.多数医学概率决策支持系统基于预期效用理论[7],试图最大程度模拟人类直觉输出良好决策,但由于过分依赖决策者的期望,故具有较大的决策波动性,未能完全达到临床决策精准诊疗的要求,误诊概率较大.
因此,以后悔理论[9]为决策评价基础,融合理性和直觉的认知情感,引入决策者的个人偏好,确定最优策略决策.通过决策曲线分析评估不同的治疗策略,采用预测模型来估计患者的疾病概率,与决策者的阈值概率比较,整合了决策者包含预后及治疗的态度和喜好的证据信息,确定决策者能够容忍的决策错误域,输出最优决策集.
本模型提出了一种引出决策者对治疗决策偏好的新方法.与传统的引导偏好方法相反,本模型考虑了潜在错误在决策中的后果,通过建立一个双重模拟量表来捕获决策遗憾错误集,评估每个可用策略的相关利弊并建立候选集,从遗憾理论的角度重新建立启发式决策曲线模型.
1 相关理论
1.1 基于预测模型的决策树理论
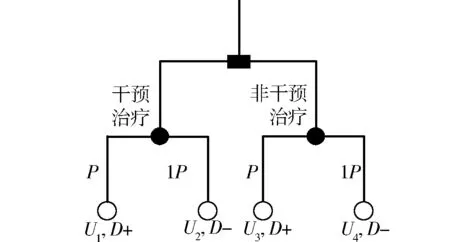
图1 治疗管理决策树Fig.1 Treatment management of decision tree
图1描述了一个典型的基于预测模型的决策树治疗模型,该模型设有两个竞争策略:治疗策略与不治疗策略,输出4个可能的组合结果:全部治疗、不治疗、模型决策必要治疗和模型决策不治疗.P=P(D+)表示与疾病相关联概率;1-P=P(D-)表示不存在疾病而诊疗的相关概率;Ui是对应结果输出,i∈[1,4],U1表示对存在疾病的病人进行治疗(必要治疗),U2表示对没有疾病的人进行治疗(不必要治疗).以下使用的术语——治疗,涉及一般意义上的保健干预,包括可能的治疗或诊断测试.
基于预测模型的概率复杂性决定了决策过程具有很大的偶然性[10].由于目前尚无对概率值规范化的决策诊疗说明,对患者的治疗主要依靠决策者本身的经验.从经典决策理论的角度来看,解决方案往往需要引入阈值概率Pt,当病人的患病概率值超过该阈值时,即可进入下一阶段诊疗.然而,在大多数情况下决策无法做到百分之百准确.因此,一旦做出决定,可能会出现错误决策,在临床诊断领域带来严重的后果.当错误决定的后果危及生命或严重影响病人的生命质量时,后悔尤其强烈.形式上,遗憾可以表示为所采取的决策行为效用与真实效用之间的差异.在决策过程中,任何一方都可能会感到遗憾,例如接受治疗的病人、病人的代理人或管理治疗的医生.假设决策者是治疗医生,采用遗憾理论估计阈值概率Pt描述两种遗憾结果:对有病患者未采取治疗和对未患有疾病者采取治疗措施.

图2 基于决策诊断的决策树后悔模型Fig.2 Decision tree depression model based on decision diagnosis注:图中P表示患病概率;1-P表示未患病概率;Pt表示治疗阈值概率;Rg表示与错误决策关联后悔函数;Rx-表示不采取治疗措施;Rx+表示采取治疗措施;D+表示患病;D-表示未患病;例如Rg(Rx+,D-)表示对未患病患者采取治疗措施的后悔值.
图2描述了基于决策结果的遗憾推导效用模型.当患病概率超过阈值概率时,遗憾值表示对患病者未采取治疗的错误后悔度.类似地,当患病概率小于阈值概率时,遗憾值表示对未患病者采取治疗的错误后悔度.Rg(RX,D+)=Rg(RX,D-)=0表示采取了正确决策,故相应遗憾度为0;(U1-U3)表示犯了有病未治的错误(称为Ⅰ类错误后果);(U4-U2)表示犯了未病有治的错误(称为Ⅱ类错误后果).基于以上假设,定义阈值概率如下:
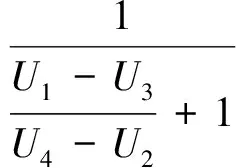
(1)
公式(1)有区别地限定了决策者采取治疗或不治疗的偏好.通过阈值概率将决策者的假阴性错误(即未能提供必要治疗的Ⅰ类错误)与假阳性错误(即不必要治疗的Ⅱ类错误)相结合.特别是当U4-U2=0时,对不必要的治疗不存在遗憾.这种情况下,Pt=100%,说明治疗只是针对患病者的确定性治疗,然而在临床诊断领域此状况属于小概率事件.
1.2 启发式阈值概率
启发式阈值概率是试图衡量决策者倾向性态度的决策理论,核心是通过捕捉决策态度,利用阈值概率规范管理策略模型.存在两类方法规范阈值概率,一类是标准规范理论、时间权衡理论,但由于时间复杂度较高且缺乏足够的认知能力,是有偏估计决策,无法有效评估决策价值,决策精度不高;另一类方法是使用评定量表,如视觉模拟评分策略,通过管理决策参与者缩减候选策略集,但受限于模拟决策尺度,不能完全实现决策状态的动态平衡.
改进的启发式阈值概率利用双重视觉模拟决策评估可能出现的失误后果.第一类用于评估决策遗憾与潜在错误之间的缺失管理;第二类是衡量决策遗憾与潜在错误之间的过度管理治疗,计算阈值概率.
采用双重模拟策略,仿照疼痛评估限制理论[ 11],利用0~100评分制描述遗憾后悔度.引入阈值概率,将医生的遗憾与错误决定(如给予不必要的治疗与过度治疗)关系数值化,这些问题可以狭义地与特定的结果(例如生存/死亡率、心脏病发作等)相关.然而,大多数治疗都与多个维度相关,要准确地取舍多领域、多维度可置换决策集,需要通过询问方式进行利弊权衡,解决认知机制中直觉与审议的双重决策过程.
对医生阈值概率的数值设定采用基于决策遗憾水平的访谈形式,获取医生对疾病诊疗结果的遗憾后悔度,核心问题如下:
(1)对0~100的任意整数,0表示没有遗憾,100表示最大遗憾,如果没有提供必要的治疗,会如何评价遗憾水平(即没有对应该治疗的病人治疗)?本问题答案可表达为公式(1)中的(U1-U3);
(2)对0~100的任意整数,0表示没有遗憾,100表示最大遗憾,如果对病人做了不必要的治疗,会如何评价遗憾水平?本问题答案可表达为公式(1)中(U4-U2).
假设医生对以上问题的回答分别是60和30,即意味该医生认为Ⅰ类错误决策发生的概率是Ⅱ类错误发生概率的2倍(60÷30=2),则该医生的阈值概率可计算为
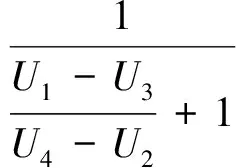
(2)
2 后悔决策曲线分析模型
决策者可能会提出许多供选择的策略,这使得决策模型计算量过大.本模型公式以Vickers[12]的决策曲线预期效用分析模型为改进对象,增加基于遗憾度的简约函数,具有额外的决策理论优势,能够在双认知水平上度量决策后果,从而描述了包含所有替代策略的广义决策树,如图3所示.

图3 治疗的广义决策树分类决策模型Fig.3 Treatment of generalized decision tree classification decision model注:图中P表示患有疾病的概率;1-P表示没有疾病的概率;Rg表示与错误决定相关的遗憾度;Rx-表示无治疗;Rx+表示治疗;D+表示存在疾病;D-表示不存在疾病.
通过求解决策树,估计与每个策略相关联的遗憾期望,模型决策后悔度函数可表示如下:
ERg[Model]=p(FN)(U1-U3)+(1-p)(FP)(U4-U2).
(3)
FN=P(p (4) 对于给予治疗和不给予治疗的决策策略,预期后悔度模型表示如下: (5) (6) 若把不给予治疗的决策策略后悔度函数看成基准策略,净期望后悔差异函数中模型决策后悔度函数,Ⅰ类错误治疗策略和Ⅱ类错误策略决策后悔度函数可表示如下: (7) (8) NERD[non-Treat,non-Treat]=0, (9) (10) 为便于分类决策时更加清晰地描述患病比例与阈值概率的相关性,分别将上述公式改写如下: (11) (12) 本模型策略集的决策响应集合采用如下规则集: (1)当计算NERD[不治疗、全部治疗]时,假设所有患者都有该疾病,所以#TP是实际患有该疾病的人数,#FP是没有该疾病但被给予治疗的人数. (2)当利用公式(11)计算NERD[不治疗,模型决策]及用公式(12)计算NERD[全部治疗,模型决策]时,计算每个阈值概率#TP,#FP,#TN,#FN,如果预测概率大于或等于阈值概率则推断患者具有该类疾病. (3)当给定阈值概率将两个策略进行比较时,NERD值提供与遗憾度相关的信息.如果NERD=0,意味着两种策略的遗憾度没有差别: NERD[策略1,策略2]=0⟺ERg(策略1)-ERg(策略2)=0⟺ERg(策略1)=ERg(策略2). (13) (4)如果NERD[策略1,策略2]>0,意味着策略2比策略1造成的遗憾度更小,优选策略2,反之亦成立: NERD[策略1,策略2]>0⟺ERg(策略1)>ERg(策略2), (14) NERD[策略1,策略2]<0⟺ERg(策略1) (15) (5)满足传递性原理(若A>B且B>C,则A>C),通过其对应的NERD数值比较每对策略,输出每个阈值概率下的最优决策: NERD[策略1,策略2]>NERD[策略2,策略3]>0⟺ERg(策略1)>ERg(策略3). (16) 基于后悔度的决策曲线分析模型算法如下: ①选择并确定阈值概率; ②假设不对患者进行治疗且p≥Pt时,计算#TP和#FP; ③使用公式(11)计算NERD[不治疗,模型决策]; ④使用公式(12)计算NERD[全部治疗,模型决策]; ⑤使用公式(11)计算NERD[不治疗,全部治疗],其中#TP是患有疾病的患者数,#FP是没有接受治疗的疾病患者数; ⑥在阈值概率范围内,重复步骤①至⑥; ⑦将步骤③至⑤中计算的NERD数值逐个与阈值概率相比较,并按规则(3)与规则(4)输出模型决策. 本模型选取男性死亡主要原因之一的前列腺癌作为说明本方法适用性的实验用例.目前,临床上对前列腺癌的主要筛查手段是前列腺癌活检.前列腺癌活检是一种侵入且不舒服的检查项目,过程痛苦且伴随有感染风险.通常,将患者是否有前列腺特异性抗原(PSA)水平升高作为重要诊断指标,然而大多数PSA高的男性并没有前列腺癌. 在统计模型的基础上增加多个预测因子(PSA、年龄、家族病史等其他标记),可预测患者是否有必要进行活检.当医生看到一个病人的PSA升高时,有3种可能的选择:活检、拒绝活检或在统计模型中查找他的患病概率,然后做出决策.依据本算法,通过比较决策集确定阈值概率不同取值条件下的最优策略.通过将每个NERD策略的特定阈值概率与公式(13)至公式(15)中的策略进行比较,实现策略优化.依据NERD[策略1,策略2]的数值,采取以下决策策略: (1)当NERD(不活检,模型决策)>0,该模型选取不活检策略; (2)当NERD(不活检,全部活检)>0,该模型选取不活检策略; (3)当NERD(全部活检,模型决策)>0,该模型选取不活检策略. 基于最优策略评价,通过比较治疗医生的概率阈值与启发规则,根据预测模型的癌症概率对比阈值概率.使用临床医生访谈方式,整体决策过程描述如下: (1)医生决策阈值概率.在0~100,将医生对Ⅰ类错误治疗策略进行评分,其中0表示对决策做出完全没有后悔的评价,100表示对决策做出最大限度后悔的评价,设置问题“如果没有提供必要的治疗,如何评价后悔水平1#医师为50,2#医师为70……”,将上述值代入公式(1)中的U1~U3.类似地,对Ⅱ类错误策略决策评分,设置问题“如果你进行了不必要的治疗,你如何评价你的后悔水平?1#医师为10,2#医师为60……”,代入公式(1)的U4-U2.计算阈值概率:1#医师为16%,2#医师为46%. (2)计算阈值概率的最佳策略.依据公式(13)至公式(15),计算#1医师在阈值概率等于16%时,通过求解不等式得到最佳决策:NERD(全部活检,模型决策)>0,策略“模型决策”优于策略“全部活检”;NERD(不活检,模型决策)>0,策略“模型决策”优于策略“不活检”;NERD(不活检,全部活检)>0,策略“全部活检”优于“不活检”. 因此,对于1#医师的临床决策而言,通过统计模型预测癌症概率的活检,最佳策略是“模型决策”,下一步是计算患者的癌症概率并将其与阈值概率进行对比.对于2#医师而言,阈值概率等于46%,最佳策略是“不活检”. 在这种情况下,计算癌症概率的引入不会影响医生决策. (3)基于统计模型计算特定患者的癌症概率.如果癌症概率大于或等于阈值概率,医生应该对患者进行活组织检查;如果癌症概率小于阈值概率,医生则不应该对患者进行活组织检查.假设特定患者的癌症概率等于20%,1#医师的阈值概率为16%,在这种情况下,1#医生考虑推荐活检,2#医生的最佳策略是建议不对任何患者进行活检. 本研究提出了一种基于后悔理论的启发式医学决策曲线分析方法,依靠遗憾理论和决策曲线分析,帮助医生在适当的医疗干预措施中进行决策选择.利用带有遗憾反馈函数的认知模型确定决策者对可用策略的偏好,做出最佳决策.从遗憾理论的角度改进了曲线决策理论,基于后悔理论的启发式医学决策曲线分析方法量化了决策者对特定策略的态度,不需要在双重处理认知系统中对每种决策单独推理. [1] 余鹰,苗夺谦,赵才荣,等.基于粗糙集的多标记决策系统知识获取方法[J].计算机科学与探索,2015,14(1):141-147. [2] 肖文军,陆茜,姚旭东,等.决策曲线分析评价临床预测模型的应用研究[J].中国卫生统计,2012,26(3):110-118. [3] 李永立,罗鹏,张书瑞.基于决策分析的社交网络链路预测方法[J].管理科学学报,2017,32(1):89-97. [4] 杨恶恶,王坚强,马超群,等.基于云发生算法的犹豫语言多准则决策方法[J].控制与决策,2015,40(2):224-231. [5] 梁海明,姜艳萍,孔德财.考虑偏好序的多满意稳定导向双边匹配决策方法[J].系统工程理论与实践,2015,15(6):135-141. [6] 张龙昌,杨艳红,赵绪辉.基于云模型的SaaS决策方法[J].电子学报,2015,32(5):98-105. [7] GREENLAND S.Bayesian interpretation and analysis of research results [J].Seminars in Hematology,2008,45(3):141-149. [8] SHRINK C A M,LUCAS P J F,HOEPELMAN I M,et al.Computer-assisted decision support for the diagnosis and treatment of infectious diseases in intensive care units [J].The Lancet Infectious Diseases,2005,5(5):305-312. [9] VICKERS A,CRONIN A,ELKIN E,et al.Extensions to decision curve analysis,a novel method for evaluating diagnostic tests, prediction models and molecular markers [J].BMC Medical Informatics and Decision Making,2008,8(1):53-60. [10]HOZO I,DJULBEGOVIC B.When is diagnostic testing inappropriate or irrational acceptable regret approach [J].Med Dec Making,2008,28(4):540-553. [11]O′CONNOR A M,LEGARE F,STACEY D.Risk communication in practice:the contribution of decision aids [J].BMJ,2003,327(7417):736-740. [12]VICKERS A,ELKIN E.Decision curve analysis:a novel method for evaluating prediction models[J].Med Dec Making,2006,26(6):565-574. Amethodofheuristicmedicaldecisioncurveanalysisbasedonregrettheory WANGKai1,LIUYuwen1,2,XUJicheng3 (1.DepartmentofHealthManagement,BengbuMedicalCollege,Bengbu233030,China; 2.SchoolofComputerScienceandTechnology,UniversityofScienceandTechnologyofChina,Hefei230027,China; 3.SchoolofInformationandComputerScience,AnhuiAgricultureUniversity,Hefei230027,China) Decision Curve Analysis has been widely used to diagnose or the evaluation predictive models. However, the core of DCA is based on the theory of expectation utility, which is also usually influenced by the intuitive system as well as the analysis and consideration of the dual cognitive system. In order to improve the accuracy of the forecasting model, this paper presents a dual simulation scale, which describes the regrettable decision function model by describing the regrettable difference operator, and describes the decision-making scheme based on the classical decision tree model. Then, the value of the difference is determined, the probability of the decision threshold is constructed, and the threshold of the potential error decision is determined. Experiments show that the model has high stability and accuracy. regret theory; decision curve analysis; double simulation scale; threshold probability TP391 A 1674-330X(2017)04-0066-06 2017-08-10 安徽省高校自然科学重点研究项目(KJ2017A223);安徽省高校自然科学一般项目(KJ2015B023);安徽省蚌埠市科技发展指导性项目(20160327) 王凯(1985-),男,安徽蚌埠人,讲师,硕士,研究方向为医学信息决策与数据挖掘.
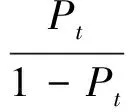
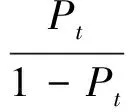
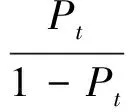
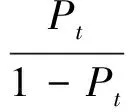
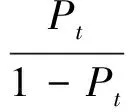
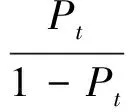
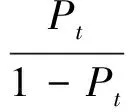

3 实验
4 结语

