圆锥曲线中与切线长相关的一组等式

江苏省常州高级中学 (213003)

陈 武

圆锥曲线中与切线长相关的一组等式

江苏省常州高级中学 (213003)

陈 武

文[1]把圆的切线长公式推广到有心圆锥曲线中.

文[2]对于双曲线的情形作出了更正与证明.

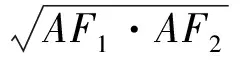
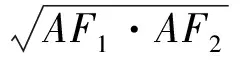
从公式中感受数学对称美、简洁美的同时，我们也自然地提出两个问题：有心圆锥曲线中是否还存在与切线长相关的其他等式；抛物线中是否也存在与切线长相关的等式.

经过探究，笔者得到以下一组与切线长相关的优美等式.

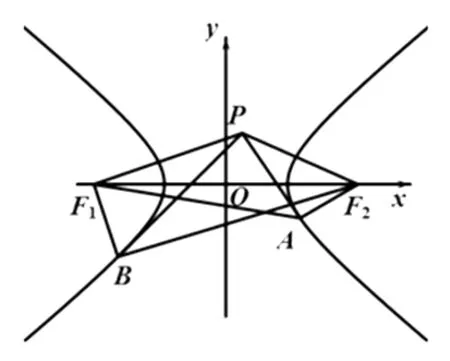
图1

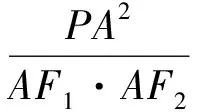
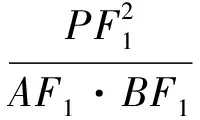
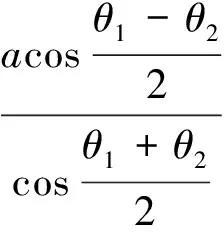
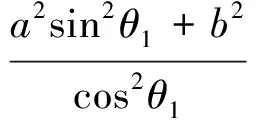
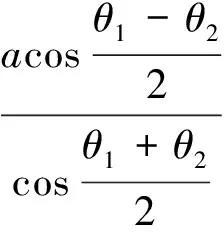
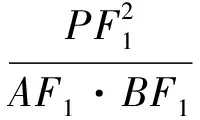
椭圆也有类似的性质，证明方法与性质1类似，不再另证.

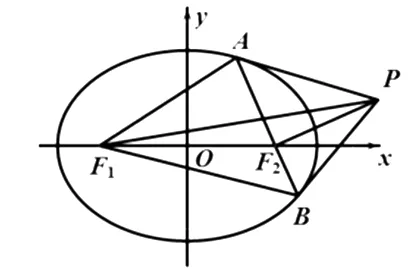
图2

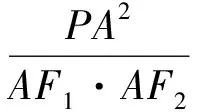
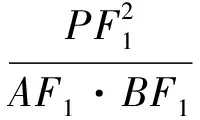
注:圆本质上是椭圆的一种退化形式(即椭圆的两个焦点重合而成圆心),因此令a=b=r,(1)式变为PA2=x20+y20-r2,这就是圆的切线长公式.

性质5 如图3，F为抛物线y2=2px(p>0)的焦点，过抛物线外一点P(x0,y0)作抛物线的切线，切点为A、B,则

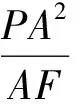
(2)PF2=AF·BF.

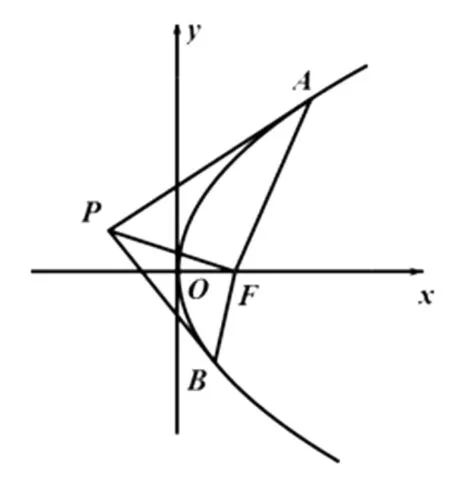
图3

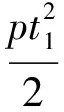
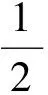
[1]徐文春.圆的切线长公式在有心圆锥曲线中的推广[J].数学通讯(下半月)，2014(9):43-44.

[2]陈海波.有心圆锥曲线的切线长公式的更正及证明[J].数学通讯(下半月)，2015(5):61-63.