浸润数学文化，培育数学素养*——“数系的扩充和复数的概念”教学实践与思考

江苏省常熟市浒浦高级中学 (215512)

殷伟康

浸润数学文化，培育数学素养*
——“数系的扩充和复数的概念”教学实践与思考

江苏省常熟市浒浦高级中学 (215512)

殷伟康

“数系的扩充和复数的概念”是高中教材中经典内容之一，富有浓厚的数学思想和数学文化，复数概念的发展具有丰厚的历史背景.由于不少教师对“问题情境的创设、数学活动的设计”认识不到位，导致复数概念教学的弱化，即复数概念的本质属性突出不够，缺乏思想方法引领，学生对虚数单位i的引入难以理解.因此，笔者从数学文化的视角出发，结合学情，运用数学史的有效融入方式，对教材进行“二次开发”，尝试“重构式”教学方法进行教学，呈现知识的自然发生发展过程，促进学生理解数系扩充的必要性、原则和复数概念的本质属性，提升学生数学核心素养.

一、创设情境，再现历史

问题1 1545年意大利数学家卡尔丹(G.Cardano，1501～1576)在《重要的艺术》一书中提出了一个问题：“将10分成两部分，使两者的乘积等于40，求这两数.”你能帮卡尔丹解决这个问题吗？

生：设所求的这两数分别为x,10-x，根据条件可得x(10-x)=40，整理得x2-10x+40=0，其判别式Δ=102-4×40=-60<0，所以方程没有实根.

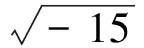
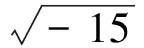
设计意图：以卡尔丹经典问题为情境引入，激发学生学习的兴趣.同时，引领学生重温历史，感悟数学发现并不神秘，数学家也是从常规问题入手.充分暴露数学家的思维过程，一方面让学生体验数学家的科研精神，另一方面让学生处于“愤悱”状态：负数能否开平方？打破原有认知平衡，形成强烈的、合乎自然的认知冲突，引发学生思考，激发学生探究新知的欲望，同时为学生更好地接受和理解虚数埋下伏笔.

二、追溯历史，总结规律

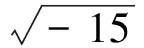
(1)从社会生活的角度来看数的发展：

(2)从数学内部的角度来看数的发展：

设计意图：学生已经学习过自然数、整数、分数、负数、有理数、无理数、实数等，在此基础上，帮助学生重新建构数集的扩充过程，即自然数集→整数集→有理数集→实数集，这是学生的“最近发展区”，也是本节课知识的生长点.

问题5 什么原因导致数的概念逐步扩充的？即每一次数系扩充的主要原因是什么？每一次数系扩充的共同特征是什么？

(1)数集的每一次扩充，可以解决某些在原数集中不能解决的矛盾，这说明数集的扩充具有“进步性”.

(2)新的数集都是在原来数集的基础上“添加”了一种新的数得来的，这说明数集的扩充具有“引新性”.

(3)数集扩充后，没有影响到原有的运算性质，这说明数集的扩充具有“可算性”.

扩充特征：①引入新的数；②原数集中的运算规则在新数集中得到保留和扩展，都满足交换律和结合律，乘法对加法满足分配律；③新数集解决了原数集一些不能解决的问题.

设计意图：通过回忆、思考每次数集扩充的必要性，解决了哪些问题，即数集为什么要扩充？每一次数系的扩充，必然伴随着运算功能的完善.通过回顾数系扩充的历程，引导学生发现数系扩充的规律，进而找到数学“发明”的灵感，有利于培养学生的归纳、概括与表达能力.

三、类比运算，构建新知

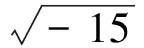
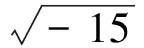
师：这样所有负数的二次根式的问题都解决了.因此问题转化为找一个数的平方为-1？

设计意图：引领学生再探卡尔丹问题，将问题转化为找一个数的平方为-1，给予学生充分思考的时空，从而让“引入新数”水到渠成.

问题7 如果想要方程x2=-1有解，你打算怎么办？

生：引进新数与新的数学符号.

师：大数学家欧拉就是这么想的，他把这个数记为i,使得i2=-1.“i”来源于英文单词“imaginary”的第一个字母，是“假想的、虚构的”意思，在数学里，我们称之为虚数单位.

设计意图：介绍与虚数单位i有关历史，强化对i的认识，并让学生感受到科学上每一步的迈进是多么艰辛！

问题8 根据数系扩充的规律，“i”既然是数就可进行运算，你能把“i”与实数进行四则运算吗？

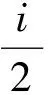
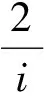
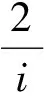
问题9 意大利数学家邦贝利在他的著作《代数学》中给出了虚数单位与实数的四则运算.那么，这些数能否有一个统一的形式？即你能写出一个形式，把刚才所写出来的数都包含在内吗？

设计意图：实数可以与i进行四则运算，进行四则运算时，原有的加法，乘法运算律仍然成立.引导学生类比实数的运算法则，由特殊到一般，抽象概括出复数的代数形式，从而完成从实数集到复数集的扩充，同时培养学生的抽象概括能力.

问题10 我们把形如a+bi(a∈R,b∈R)的数叫复数，通常用字母z表示，即z=a+bi(a,b∈R)，其中a叫做z的实部，b叫做z的虚部.如何阐述复数a+bi(a,b∈R)的几何直观解释？

1806年瑞士数学家阿尔冈将复数a+bi(a,b∈R)表示为平面上的向量，这就提供了表示向量及其运算的一个代数形式，能够通过复数代数地研究向量.1831年高斯公开描述复数的几何意义，他将复数a+bi(a,b∈R)解释为复平面上一个点(a,b)，而且阐述了复数的几何加法与乘法法则.从此，复数开始表示向量，在水力学、地图学、航空学中均有着广泛应用.1843年英国数学家哈密顿创造了“四元数”，间接地推动了向量代数和向量分析的创立.这样复数的直观意义就建立起来了，使学生清楚地认识到“虚数不虚”.

问题11 形如a+bi(a,b∈R)的数一定是虚数吗？它会是实数吗？

当b=0时，a+bi(a,b∈R)表示实数；当b≠0时，a+bi(a,b∈R)表示的数我们称为虚数，在虚数中，当a=0时，我们把bi(b∈R且b≠0)称为纯虚数.

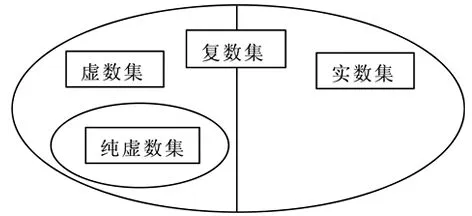
图1

问题12 复数集与实数集、虚数集、纯虚数集之间有什么关系？

设计意图：引导学生自然而然对复数进行分类，通过学生自主探究，找到复数分类标准，解决复数的分类问题，加深对复数概念的理解.并采用概念同化的方式完善学生的认知结构.

四、数学运用，深化概念

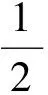
例2 实数m是什么值时，复数z=m+1+(m-1)i是：(1)实数?(2)虚数?(3)纯虚数?

例3 已知(x+y)+(x-2y)i=(2x-5)+(3x+y)i，求实数x，y的值.

设计意图：巩固复数的分类标准，促进学生对复数概念的理解.事实上，复数概念的抽象性特征决定了只有通过适当的练习，才能深刻理解复数概念和运算规律.通过例3，让学生掌握处理复数问题的基本思想“复数问题实数化”，运用复数相等的定义，将一个复数方程转化为两个实数方程进行求解.

五、思想与文化并重，探究与素养并行

复数的产生和发展是数学家们辛勤耕耘的结果，是思想观念的一种突破.在“数系的扩充”教学设计中，依据认知的历史发生原理，数的发展过程与学生认知发展关系，结合数学史，对教材进行“再创造”，让学生亲身经历探究复数概念产生、发展过程，体会到其中蕴含的数学思想，品味数学文化的内涵，培育理性精神，提升学生的数学素养.

1.渗透数学思想，感悟数学文化

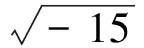
2.凸显数学文化，彰显数学本质

数学知识是数学家思维活动的成果，数学家的思维方法和思维过程是数学文化中的宝贵财富.因此，教师要从数学文化的视角，发掘复数概念形成过程中数学家思维活动方式，利用数学家的思考方式和方法来突破复数概念这一教学难点.创设充满浓郁数学文化的问题情境，以卡尔丹问题引入新课，让学生产生强烈的认知冲突，经历数学家曾经经历的困惑，凸显引入新数、扩充数系的必要性，从而诱发学生深入思考与探究.回顾数系的扩充过程，引导学生思考：每次扩充引入了什么数？解决了什么实际问题？它们有什么共同特点？提炼出数系扩充的“进步性、引新性和可算性”原则，为后面的探究活动作必要的铺垫.引导学生根据前三次数系扩充的一般规律，运用类比方法，模仿数学家欧拉的想法，合理引进虚数单位i.揭示数系扩充的本质特征，逐步领悟数系扩充过程的研究方法，学会用数学的思维方式去思考问题、分析问题和解决问题.

3.促进深度思考，提升核心素养

数学核心素养可以理解为学生学习数学应当达成的有特定意义的综合性数学能力，是数学的教与学过程应当特别关注的数学基本素养.数学核心素养的发展，自然体现在学生再创造复数过程中.复数概念的发现过程是典型的数学抽象过程.引导学生从历次数系扩充过程中抽象出数系扩充过程的研究方法：引入一种新的数，就要定义相应的运算；定义一种运算，就是要研究它满足怎样的运算律.再引导学生抽象概括出数系扩充过程的基本原则：使算术的运算律保持不变.通过问题6-10的探讨，引导学生深度思考，运用类比、归纳方法，合理地引入虚数单位i，并抽象出复数的代数形式，从而构建复数概念，培养学生数学抽象、逻辑推理等数学核心素养.

[1]仓万林.课堂视角下的数学文化行动研究[J].上海中学数学,2014(9)：4-7.

[2]林京榕.渗透数学文化 发展核心素养——以“数系的扩充和复数的概念”教学为例[J].福建中学数学,2017(7)：19-21.

本文系江苏省教育科学“十二五”重点资助课题：构建数学文化课堂的教学实践研究(课题批准号B-a/2013/02/069)研究成果之一.