基于混合编码遗传算法的最优跟踪门

赵 菡, 张 琤, 林家骏

(华东理工大学信息科学与工程学院,上海 200237)

基于混合编码遗传算法的最优跟踪门

赵 菡, 张 琤, 林家骏

(华东理工大学信息科学与工程学院,上海 200237)

跟踪算法优化可以提高跟踪质量,选择恰当的跟踪门是优化跟踪算法的关键措施之一。本文提出了一种基于混合编码的遗传算法,用于杂波环境下目标跟踪过程中跟踪门参数的离线优化。该算法将二进制编码与浮点数编码结合,对跟踪门的形状和大小进行混合编码,选择跟踪精度性能指标构造遗传算法的适应度函数,以此将跟踪算法的优化问题转化为遗传算法寻优,在不同杂波环境下优化跟踪门参数设置。

目标跟踪; 跟踪门; 遗传算法; 混合编码

跟踪门的形成是多机动目标跟踪过程中首当其冲的问题,选择恰当的跟踪门能减少数据错误关联的次数,提高目标跟踪精度[1]。但目前聚焦跟踪门的研究并不多见,在为数不多的研究中,有学者提出了跟踪门的自适应设计方法[2-3];有研究通过计算性能评价函数的最优值以逆向推算跟踪门的尺寸[4];还有文献[5]提出采用数论法,根据测量误差和状态估计误差设计跟踪门。这些研究基本集中在如何设定、调整跟踪门的大小,忽略了跟踪门形状对于跟踪质量的影响。

选择恰当的跟踪门可理解为是对跟踪门算法的优化,因此可当作目标跟踪算法管理的一个部分。而算法管理的实质是一种优化过程,从理论上说现有的优化算法均可考虑用于算法管理[6]。算法管理可以分为3个层次:算法的参数设置、单点步骤上的算法选择、多个步骤上的算法组合。本文借助遗传算法,通过将跟踪门形状和大小进行混合编码,实现对跟踪门的形状和大小整体优化。同时选择细粒度性能指标构造适应度函数,该指标能较灵敏地体现出参数变化对于跟踪性能的影响,实现了算法参数层面的优化。

1 航迹跟踪算法与跟踪门

1.1 状态估计与数据关联

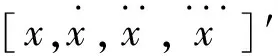
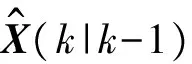
(1)

观测向量的一步预测为

(2)

卡尔曼滤波增益矩阵为

(3)

对应的新息协方差为

(4)

则第i个候选回波的目标状态估计为

(5)

假设跟踪门总共选中了mk个候选回波,计算每个候选回波来源于真实目标的互联概率βi(k),然后对所有候选回波加权求和得到状态更新方程:

(6)

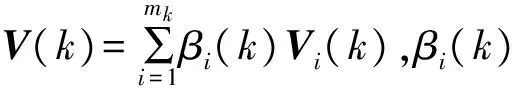
1.2 跟踪门理论

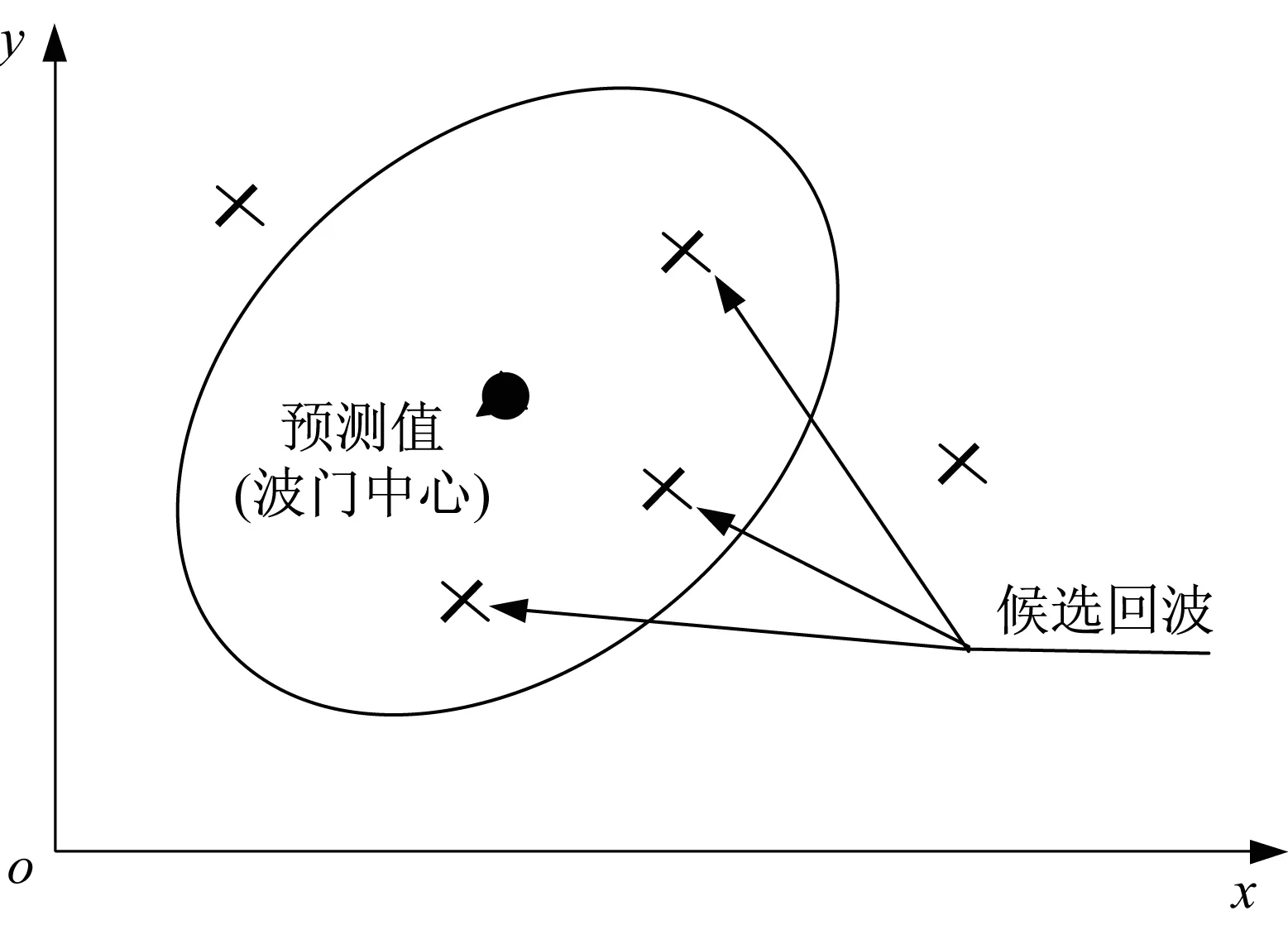
图1 椭圆门示意图Fig.1 Elliptic gate schematic diagram

2 基于遗传算法的波门寻优实现

2.1 混合编码实现

跟踪门的形状和门限常数分属不同的数据类型,要兼顾遗传算法运算的精度和速度,考虑对上述两个参数采用混合编码。波门形状采用二进制编码,门限常数采用浮点数编码[10]。个体混合编码后的基因串包含两类参量,即G=[GS,GL],如图2所示。其中GS为跟踪门形状的二进制编码,GL为门限常数的浮点数编码。

图2 混合编码基因串Fig.2 Gene string by hybrid coding

2.2 算法描述

遗传算法的寻优建立在目标跟踪这一动态系统上,寻优过程如图3所示。将初始种群中个体对应的跟踪门参数G作为初始化设定输入系统,根据输出的跟踪航迹与真实航迹的误差,标定个体适应值。经遗传操作后产生的新个体,在保持其余参数不变的情况下,作为参数设定输入系统,进行新一轮的适应值计算和种群更新,系统的停止判据为达到系统迭代条件或者满足一致性条件。

由此可见,混合编码遗传算法与目标跟踪系统形成了闭环寻优系统。遗传算法对跟踪过程中的一个环节进行优化,其优化目标和整个跟踪系统的优化目标一致。用于指导遗传操作的适应值并非经数学运算得到的代数值,而是在目标跟踪动力学系统生成跟踪误差的基础上得到。这种思路有效地将多目标优化问题转化为单目标优化,为今后进一步优化跟踪系统中的其他参数和算法模块提供了参考。

图3 基于混合编码遗传算法的跟踪门寻优流程图Fig.3 Flow chart of tracking gate optimization based on hybrid coding genetic algorithm

2.3 Hellinger距离与适应值计算

常用的航迹误差指标有:位置均方根误差(PRMSE)、马氏距离、Hellinger距离等。其中,Hellinger距离考虑了协方差的影响,解决了PRMSE在状态估计相同、不确定度不同的情况下难以区分的问题,具有较高的精确度和敏感度,选择其作为跟踪误差的评估指标[11]。

若两个概率分布f=N(x,Σx)、g=N(y,Σy)均服从高斯分布,其Hellinger距离有如下的形式:

(7)

在目标跟踪系统中,可以将(x,Σx)看成真实的状态向量分布,将(y,Σy)看成估计的状态向量分布,对于真实的状态向量,其不确定度可以作为一种基准应该具备最优的特性,选用克拉美罗下界(Cramer-Rao)[12]。若用Hellinger距离dH|k(f,g)表示k时刻真实航迹和估计航迹之间的距离,可构造如下的适应度函数:

(8)

用BL与BU分别表示预设的门限常数上界和下届,则跟踪门优化问题可转化为

G=argGmaxffitness(G)

(9)

s.t.G=[GS,GL]

GS∈{0,1}

BL≤GL≤BU

GL,BL,BU∈R

2.4 遗传操作

遗传算法中需要通过选择、复制等来保证最优个体不被交叉、变异等遗传运算破坏。本文采用最优保存策略进化模型,先计算种群中每个个体的适应度比例,通过轮盘赌的方式,使拥有更大适应度比例的个体有更大的概率遗传到下一代的种群[13]。

针对混合编码方式,交叉操作分为两种:代表跟踪门形状的的二进制编码采用单点交叉,代表门限常数的浮点数编码采用非均匀算术交叉,变异操作也相应地分为单点变异和非均匀变异两种。

3 仿真研究

3.1 参数设置

仿真剧情是不同杂波环境下高机动的单目标跟踪,目标的初始状态为[4.92 km,-79.4 m/s,0,0;0.891 km,94.6 m/s,0,0],种群规模为20,交叉概率pcrossover=0.6,变异概率pmutate=0.01。跟踪系统的采样为114个点,采样间隔为1 s,仿真次数为50。设定目标的检测概率PD=0.98,虚假量测在以正确量测为中心的正方形区域内随机均匀产生,虚假量测总数nc=λAv,其中λ是杂波密度,Av为区域的面积。本文分别给出了λ=2和λ=20,即稀疏杂波和密集杂波两种剧情。

3.2 实验结果与分析

稀疏杂波环境下跟踪门参数收敛于014.217,根据混合编码规则可知,01代表跟踪门形状的二进制编码,对应的为椭圆门;4.217代表跟踪门门限常数的浮点数编码,表示寻优结果是门限常数4.217的椭圆门。在这样的参数设定下,得到的Hellinger距离为0.173 5。

密集杂波环境下跟踪门参数收敛于016.145,同理可知寻优结果是选择门限常数6.145的椭圆门,相应的Hellinger距离为0.202 4。保持目标检测概率不变,杂波密度增大要求跟踪门相应增大,实验结果与此结论相符。

限定跟踪门的形状,依次用遗传算法仅对门限常数寻优,可得到不同形状跟踪门所对应的最小跟踪误差,实验结果如表1所示。由表1可见,在两种杂波环境下,采用混合编码遗传算法寻优结果的系统,其跟踪误差最小,系统跟踪精度最高。

进一步对比椭圆门和矩形门的实验结果,相同门限常数时两种跟踪门得到的误差虽然相差不大,但矩形门对应的面积远远大于椭圆门,在检测概率和杂波密度已定的前提下,跟踪门面积的增加必然导致计算量增大。

表1 跟踪门参数及跟踪误差统计表

3.3 跟踪门优化结果适应范围

实际目标跟踪过程中,受到的干扰不会是一成不变的。为测试本文提出的优化算法对于干扰变化具备一定的容忍度,将优化结果运用到不同杂波环境中。对比跟踪航迹与真实航迹,在一定的干扰变化范围内,跟踪系统仍能得到较理想的跟踪效果。如图4所示,将杂波密度为20环境下的寻优结果,运用在杂波密度为30的环境中,跟踪航迹与真实航迹吻合度较高。但由图5可见,当杂波密度继续增加为50时,跟踪航迹较真实航迹出现了较大偏差,尤其在目标拐弯等较大机动处。

图4 杂波密度30时跟踪效果图Fig.4 Tracking with clutter density of 30

图5 杂波密度50时跟踪效果图Fig.5 Tracking with clutter density of 50

4 结束语

针对杂波环境下的高机动目标跟踪,本文采用二进制和浮点数混合编码,将不同类型的跟踪门参数作为遗传算法优化对象,通过离线仿真得到其最优解。验证了杂波噪声与该环境下最优跟踪门之间存在一定关系,对于杂波环境下目标跟踪系统精确性的提高有着积极意义。

本文仅对跟踪门的两个参数进行寻优,影响跟踪性能的因素还有很多,细粒度来说有机动频率、量测噪声、过程噪声等,粗粒度来说有数据关联算法、机动模型、滤波算法等,更多参量的寻优需要进一步的探讨。另外,本文中的寻优结果是离线得到的,实验对象为单机动目标跟踪,多目标跟踪当中的跟踪门选取问题往往更加复杂,如何做到实时在线优化跟踪门也是需要研究的问题。

[1] 周宏仁,敬忠良,王培德.机动目标跟踪[M].北京:国防工业出版社,1991:200-217.

[2] 董国,岳三创.航迹预处理中相关波门研究[J].现代电子技术,2012,35(13):19-21.

[3] 靳标,纠博,苏涛.一种用于杂波中机动目标跟踪的自适应关联波门设计方法[J].西安交通大学学报,2014,48(10):40-46.

[4] 王明辉,游志胜,赵荣椿,等.性能优化的跟踪门算法[J].电子学报,2000,28(6):8-12.

[5] 张志芬.基于数论法的跟踪门计算方法研究[J].宇航学报,2009,30(2):725-729.

[6] 姜丽,林家骏.信息融合系统中的算法管理理论研究[J].火力与指挥控制,2009,34(5):105-108.

[7] KISHORE M,PRAVAS R.A jerk model for tracking highly maneuvering targets[J].IEEE Transactions on Aerospace and Electronic Systems,1997,33(4):1094-1105.

[8] WANG Xuezhi,CHALLA S,EVANS R.Gating techniques for maneuvering target tracking in clutter[J].IEEE Transactions on Aerospace and Electronic Systems,2002,38(3):1087-1097.

[9] 张洁,林家骏,陈小伟.跟踪门对多目标跟踪系统性能的影响[J].华东理工大学学报(自然科学版),2006,32(12):1468-1471.

[10] 范虹,孟庆丰,张优云.用混合编码遗传算法实现匹配追踪算法[J].西安交通大学学报,2005,39(3):295-299.

[11] 王晓璇.目标融合航迹质量评估方法[J].指挥信息系统与技术,2012,3(2):17-22.

[12] 郑永隆.位置级信息融合算法细粒度性能研究[D].上海:华东理工大学,2013.

[13] 周明,孙树栋.遗传算法原理及应用[M].北京:国防工业出版社,1999:32-41.

OptimalTrackingGateBasedonHybridEncodingGeneticAlgorithm

ZHAOHan,ZHANGCheng,LINJia-jun

(SchoolofInformationScienceandEngineering,EastChinaUniversityofScienceandTechnology,Shanghai200237,China)

The track qualities can be depended on tracking algorithm optimization.One of the essential optimization problems in tracking is gate selection.In this paper,a hybrid encoding genetic algorithm is proposed to off-line optimization of tracking gate parameters for maneuvering target tracking in clutter.Binary string and floating-point string represent shapes and size of tracking gate respectively.Hellinger distance is chosen for performance evaluation of tracking and can be core part of the fitness function of genetic algorithm.Generally speaking,the tracking system optimization can be converted into genetic algorithm optimization,then the tracking gate parameters can be efficiently tuned in different scenarios.

target tracking; association gate; genetic algorithm; hybrid coding

1006-3080(2017)06-0844-05

10.14135/j.cnki.1006-3080.2017.06.014

2017-06-13

赵 菡(1980-),女,安徽蚌埠人,副教授,博士生,主要研究方向为信息融合性能评价和目标跟踪算法优化。E-mail:lotus@ecust.edu.cn

林家骏,E-mail:jjlin@ecust.edu.cn.

TP391

A