换热器壳体不均匀温度场的热应力解析分析
陈孙艺,卢学培,许 敏,吴恩覃
(茂名重力石化机械制造有限公司 广东茂名 525024)
换热器壳体不均匀温度场的热应力解析分析
陈孙艺,卢学培,许 敏,吴恩覃
(茂名重力石化机械制造有限公司 广东茂名 525024)
为了评估固定管板式换热器壳程圆筒体的安全强度,针对换热器壳体中的周向、轴向和径向三维不均匀温度场,总结了根据各自一维温度场模型由相应的解析式求解其热应力的方法。该方法简单易行、安全可靠,可便捷地得到比通常有限元应力分析方法更经济合理的设计结果。案例分析表明,一般的换热器圆筒体周向温差引起的轴向热应力大于轴向温差引起的轴向热应力,且该轴向应力可能出现拉应力和压应力交替间隔分布的状况。
热应力;换热器;非均匀温度场
在对焊接管接头需要进行应力消除的固定管板式换热器进行整体热处理时,由于管束中间与壳体之间存在一定的温差,升温和降温过程的热应力作用方向相反,应校核其大小并控制不超过0.8ReL[1]。有的换热器在运行过程中同时存在压力、力矩、温度、位移等载荷,载荷的均匀性对实体受力有直接影响,而载荷的分布又与流体力学关联,外在形态不直观,隐于工程实际。一些采用简化的有限元分析设计的列管式换热器管板也会出现开裂泄漏失效,因此人们十分关注管板的优化设计,并对固定管板式换热器的温差热应力进行数值分析[2- 4],其中冷纪桐等[3]仅考虑稳态热传导在轴向的不均匀温度分布,先根据Fluent计算结果拟合出温度函数关系式作为换热器各个壁面的温度载荷,然后在基于ANSYS软件的整体换热器分析模型中进行载荷施加,分析发现实际换热器工作时的温度场以及热应力分布比当时已有文献中阐述的要复杂,换热器在并不太高的工作温度载荷下,固定管板中仍然产生了很大的热应力。与此同时,人们普遍忽视换热器壳体上的热应力,一般也就是分析由于壳壁内外温差引起的热应力[5],其实换热器的失效与数量诸多而关联密切的零部件结构、不均匀而且动态变化的载荷有重要的关系。
GB/T 151—2014明确提出,换热器设计时应考虑膨胀量不同引起的作用力,但是没有给出具体的热应力解析式。目前,设计者可便捷地应用SW6软件进行换热器结构强度设计计算,大多数案例分析一般只简化考虑管程和壳程之间的热位移无法协调而释放的热应力,并且只考虑平均金属温度,而忽略类似图1所示由于进出口非对称、流态非均匀性引起的不均匀温度场。当流场存在明显的非均匀温度场时,则需采用软件进行流场或流固耦合温度场的有限元分析,进而计算出热应力,但这给没有掌握有限元分析软件的设计者带来困难。因此,有关标准、结构不连续的计算软件和针对模型连续结构的有限元应力分析软件都不能简便地解决内压和不均匀温度场引起的换热器壳体强度的校核问题。

图1 壳体进出口非对称换热器
有学者经深入分析后发现,单独考察壳程一侧,其轴向或周向热的非均匀工况也会引起热应力并提出了计算式[6- 7]。为探讨壳程不均匀温度场对设备安全的影响,以某固定管板换热器壳体结构(图2)和表1所示工况参数为例进行分析计算。
表1 换热器设计参数

项目壳程管程设计压力/MPa4.05.0操作压力/MPa3.84.8设计温度/℃240410操作进(出)温度/℃220(240)400(245)壳体内直径/mm12001200壳体壁厚/mm2634壳体长度/mm7200800壳体材料Q345RQ345R

图2 固定管板换热器结构示意
1 壳程周向非均匀工况的热应力分析
1.1 筒体温度分布模型
壳程底部一进、上部两出的流程会引起横截面介质物性不均匀;壳体中间设有一个调节管程流体的圆筒,从左边管箱进来的部分管程介质可通过该圆筒直接从右边管箱出去,避免壳程超温。分析该结构可建立面对称流程和温度分布模型(图3),沿着箭头走向的流程在壳体横截面上引起面对称的周向温差,该温差也能引起轴向热应力。李江[7]推导了卧式蒸压釜端面无约束的筒体其壁面温度以某一过中心线的平面对称分布且分布函数为圆周角的单值函数时轴向应力及由此引起的挠度的计算式。

图3 壳体流程

(1)

(2)
σiz=Eα(Tm+acosφi-Ti)
(3)

(4)
式中:Tm——平均温度;
Ti——圆筒体上沿着圆周方向第i个测温点处的温度;
a——分布系数;
φi——圆筒体周向第i个测温点处与筒体横截面对称轴的夹角;
σiz——轴向应力;
E——圆筒体材料的弹性模量,在温度范围内为定值,此处根据平均温度查GB 150.2—2011中的表B.14,取1.89×105MPa;
α——圆筒体材料的线膨胀系数,在温度范围内为定值,此处根据平均温度查GB 150.2—2011中的表B.13,取1.242×10-5mm/(mm·℃);
wmax——筒体扰度;
L——圆筒体长度;
Di——圆筒体内直径;
δ——圆筒体壁厚,取有效厚度,钢板负偏差C1=0.3 mm,腐蚀裕量C2=3.0 mm,则δe=δn-C1-C2=22.7(mm)。
取n=5,即沿壳体周向单侧有5个测温点;设进出口温差ΔT=20 ℃,沿壳体周向线性分布,有关参数及应力见表2。
表2 有关参数及应力

测温点iϕi/(°)Ti/℃σi/MPa10220-2.0245225-62.63902300.04135235-298.45180240-49.1
把有关参数代入式(1)计算得平均温度Tm=230 ℃;把有关参数代入式(2)计算得分布系数a≈-10.827 8 ℃。
1.2 筒体轴向热应力分析
把有关参数代入式(3)可得:σ0≈-2.0 MPa,σ45≈-62.6 MPa,σ90≈0 MPa,σ135≈-298.4 MPa,σ180≈-49.1 MPa。
由此可见,该案例各个测温点的轴向热应力都不是拉应力,且第4个测温点的轴向压缩应力σ135≈-298.4 MPa,已经达到设计温度下材料许用应力(根据GB 150.2—2011中的表2,[σ]240=159.6 MPa)的187%。测温点1的σ0较小,如果壳体周向5个测温点的温差增大,若操作不稳定,冷油以T1<220 ℃的温度进入壳程的测温点1,热气同时以更高的温度进入管程,则平均温度Tm有可能高于测温点1温度(T1),从而使σ0>0 MPa,出现轴向拉应力,导致壳体中的轴向热应力交替出现拉应力和压应力间隔分布的复杂状况。
1.3 筒体挠度分析
将有关参数代入式(4),得wmax≈1.43 mm。
该挠度值虽然不大,但如果换热器壳体无法自由变形,由此而与管束之间产生不协调的弯曲热应力,将使壳体中的热应力进一步复杂化。
1.4 案例比较
对电站锅炉汽包壁温度变化引起的热应力进行分析[8- 9],汽包上下壁温差引起的热应力主要是轴向应力,切向和径向应力与之相比低一个数量级,故可忽略不计。汽包上部壁温高,金属膨胀量最大,下部壁温低,金属膨胀量相对较小,这就造成汽包上部金属膨胀受到限制而产生压缩应力,下部金属产生拉伸应力。热应力与温差成正比,汽包上下壁温差越大,产生的热应力越大。可采用简化的计算式[8]进行计算:

(5)
式中:Δθ——汽包上下侧平均壁温差,此处Δθ=ΔT=20 ℃。
其他参数同前,则σ≈1.18 MPa。
以茂名热电厂3#炉汽包为例进行热应力计算[9]。根据实测,锅炉熄火后Δθ可达50 ℃,由上下壁温差引起的轴向热应力是周向角θ的函数,当θ≈40°时轴向应力最大(34.91 MPa)。
2 壳程轴向非均匀工况的热应力分析
分析图1,可判断壳程结构沿着轴向左右对称,但由于受单一管程的影响,从左端管箱进入管束的高温介质经与壳程介质换热后从右端管箱出去,使得壳程工况沿着轴向是左右不对称的,壳程左端出口温度如果满足操作要求,肯定高于壳程右端的出口温度。方子风[6]推荐了由苏联或日本学者分别报道的同一成果,即圆筒体或管子中长度为ΔH的局部一段存在按直线分布从t2降至t1的温度变化时,在圆筒体或管子的高温边界t2处引起的轴向应力σ的计算式为:
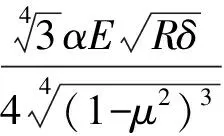
(6)
式中:R——取0.5D,D为圆筒体直径;
δ——圆筒体壁厚;
ΔT——轴向温差,ΔT=t2-t1;
α——圆筒体材料线膨胀系数;
E——圆筒体材料弹性模量;
μ——圆筒体材料泊松比。
此处ΔHz=0.5L(L为非均匀温度场圆筒体长度),其他符号同前。把有关参数代入式(6),得σ≈0.6 MPa。
按常识,圆筒体温度较高段的直径增大要比温度较低段的直径增大小,由此轴向温差在壳壁上引起的热应力是一种弯曲应力。尽管方子风[6]未说明式(6)的应力是拉应力还是压应力,是位于内壁还是外壁,但是从整体结构上的轴向平均温度分布而言,该案例的热应力不大,因此这里视之为横截面上的拉应力。
同理,就壳程进出口进行分析,在同样的进出口温差ΔT=20 ℃下,筒体两端一进一出的接口布置改为一进两出,虽然可使式(6)的ΔT/ΔHz提高1倍,轴向热应力也提高1倍,但是该案例的热应力不大,这种改变对壳体热应力影响很小。如果壳体局部区域存在显著的轴向温差,则轴向热应力才值得关注。
3 壳壁径向温差引起的热应力
壳壁外设有保温层,壳壁径向温差为ΔTj=10 ℃。参考厚壁圆筒体的热应力计算式[10],由此引起内壁面的轴向热应力和周向热应力为:
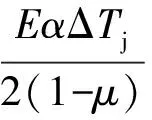
(7)
外壁面的轴向热应力和周向热应力为:
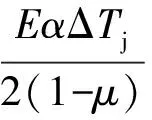
(8)
式(7)和式(8)中,筒体外内直径比K=1 226/1 200≈1.022,其他符号同前。把有关参数代入式(7)和式(8),计算得:σin- jz≈-17.0 MPa,σout- jz≈16.7 MPa。
4 内压在壳壁引起的应力及总应力分析

上述各项应力分项及其组合的总应力汇总列于表3。
表3 各项应力分项及其组合的总应力汇总 MPa
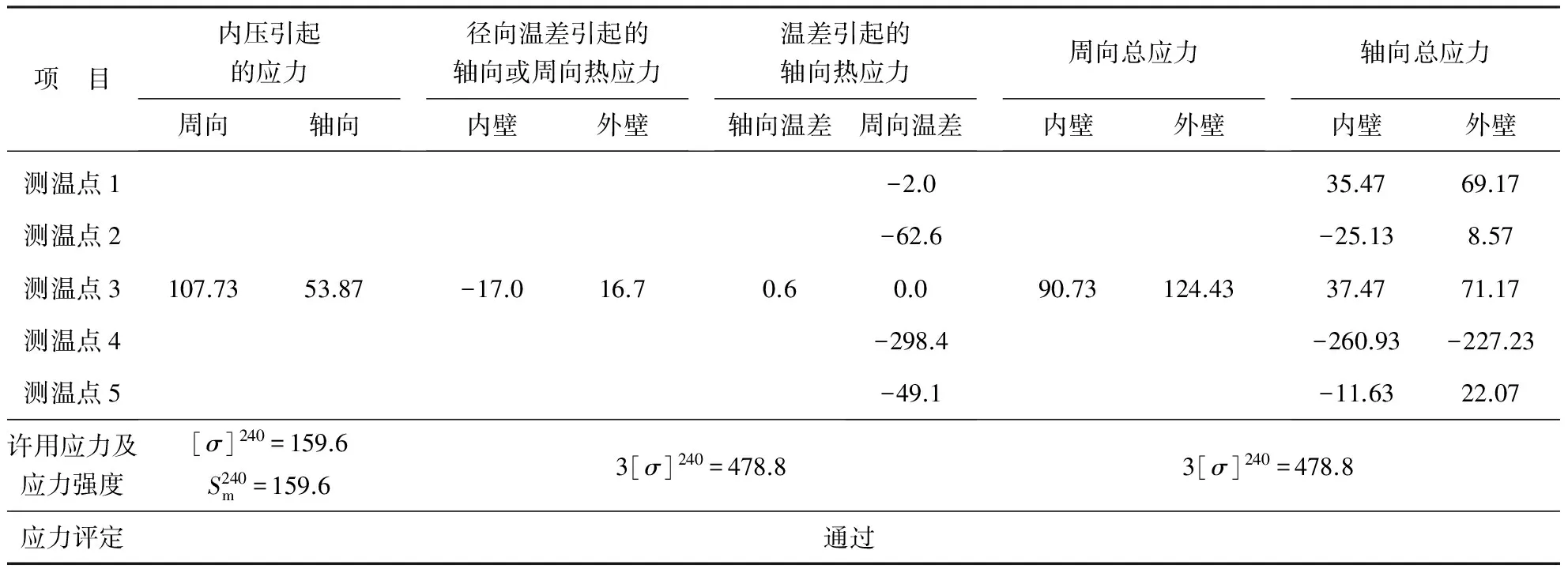
表3中筒体材料的设计应力强度系查标准JB 4732—1995中的表6- 2而得,与许用应力相等。分析表3,各项应力分项及其组合的总应力都小于所对应的许用应力或设计应力强度,图1和表1案例的强度校核通过。
一般换热器热应力水平不会超过3[σ],这也是GB/T 151—2014等标准中通常没有具体的热应力计算方法及解析式的原因之一,其对总应力的影响还与内压引起的应力水平有关。如果较高的内压已经引起较高的一次应力,则热应力可能使总应力超出许用应力或设计应力强度,从而使结构强度校核无法通过。因此,为安全起见,换热器设计中应对显著的热应力进行分析评定。
虽然热应力属于二次应力,具有自限性,但是只有热位移完全得到满足、热应力完全释放后,全长轴向的应力才降为零。圆筒体周向温差引起的轴向热应力是由圆筒体自身的热变形约束引起而无法释放,该轴向应力可能交替出现拉应力和压应力间隔分布的状况,其中的压应力可抵消内压引起的部分轴向薄膜应力的作用,使得结构更加安全。虽然较高的轴向热应力使圆筒体有潜在失稳的可能,但管束及其折流板对圆筒体有很好的支撑和抵御失稳的作用,而周向温差引起的轴向热应力中的拉应力部分会强化轴向薄膜应力的作用,使得结构可能偏危险。
图2结构的实物如图4所示,按上述计算方法校核设计的换热器壳体运行正常。在设计管束时,已使油品的流程温度场分布更缓和,其中主要是使周向温度分布得到缓和,其次使轴向温度分布得到缓和,故现在的进出口布置通过管束结构设计得到优化。

图4 换热器实物
5 结语
过去主要关注固定管板式换热器的轴向温度场及其热应力,这是有失偏彼的。换热器壳体中的周向、轴向和径向不均匀温度场所引起的热应力不一定非要采用复杂而费时的有限元模型来计算分析,除该数值方法之外,还可根据简化模型由相应的解析式求解和初步评定。总结文中分析可得:①一般换热器圆筒体周向温差引起的轴向热应力大于轴向温差引起的轴向热应力,且该轴向热应力可能出现拉应力和压应力交替间隔分布的状况,如果较高的内压已经引起较高的一次应力,换热器设计中应对显著的热应力进行分析评定。②换热器筒体两端一进一出的接口布置改为一进两出的接口布置后,使轴向热应力略有增大,但影响很小。固定管板式换热器壳体设计为筒体两端一进一出的接口布置,将使流程温度场分布更缓和,轴向热应力也得以降低。
[1] 李世玉.压力容器设计工程师培训教程[M].北京:新华出版社,2005.
[2] 章茹,黄文瀛.单程固定管板式换热器温差应力的计算[J].南昌大学学报(工科版),2003(3):70- 76.
[3] 冷纪桐,吕洪,章姚辉,等.某固定管板式换热器的温度场与热应力分析[J].北京化工大学学报(自然科学版),2004(2):104- 107.
[4] 郭崇志,周洁.固定管板式换热器的温差热应力数值分析[J].化工机械,2009(1):41- 46.
[5] BHADURI S,曾纪荣,陈秋霞.计算圆柱形筒体热应力的简便方法[J].化工设备与管道,1981(1):43- 45.
[6] 方子风.化工设备设计全书:废热锅炉设计[M].上海:上海科学技术出版社,1989.
[7] 李江.蒸压釜变温应力及变形的分析与计算[J].压力容器,1988(6):31- 34.
[8] 王国友,李海峰,李拥新,等.电站锅炉汽包热应力的产生及控制[J].黑龙江电力,2005(5):368- 371.
[9] 陈其忠.电站锅炉汽包热应力的产生及控制[J].广东电力,2001(6):5- 8.
[10] 余国琮.化工容器及设备[M].北京:化学工业出版社,1980.
AnalyticalAnalysisofThermalStressonNon-UniformTemperatureFieldofHeatExchangerShell
CHEN Sunyi, LU Xuepei, XU Min, WU Entan
(The Challenge Petrochemical Machinery Corporation of Maoming, Maoming 525024, China)
In order to evaluate the safety strength of cylindrical shell of fixed tube- sheet heat exchanger, in connection with three-dimensional, circumferential, axial and radial direction, non- uniform temperature field of heat exchanger shell, the method calculating thermal stresses corresponding to each of their one-dimensional temperature field analytic equation respectively is summarized. This method is not only simple and reliable but also can be applied conveniently to get a more economic and more reasonable design result than that obtained with common finite element stress analysis method. The result of this case shows that the axial thermal stress caused by circumferential temperature difference is higher than that caused by axial temperature difference, and that axial thermal stress may distribute in a state that tensile stresses and compresses stresses occur alternately.
thermal stress; heat exchanger; non- uniform temperature field
本文作者的联系方式:chensy@cpm.com.cn
TQ051.5
A
1006- 7779(2017)05- 0022- 05
2016- 04- 05)

