钢筋混凝土弹塑性损伤本构模型*

展婷变， 宁建国， 王志华， 任会兰

(1. 中北大学 机电工程学院， 山西 太原 030051；2. 北京理工大学 爆炸科学与技术国家重点实验室， 北京 100081；3. 太原理工大学 材料强度和结构冲击山西重点实验室， 山西 太原 030024)

钢筋混凝土弹塑性损伤本构模型*

展婷变1， 宁建国2， 王志华3， 任会兰2

(1. 中北大学 机电工程学院， 山西 太原 030051；2. 北京理工大学 爆炸科学与技术国家重点实验室， 北京 100081；3. 太原理工大学 材料强度和结构冲击山西重点实验室， 山西 太原 030024)

钢筋混凝土在加载过程中内部应力应变是不均匀的， 因而很难通过试验直接得出本构关系. 为了避开非均匀性对研究本构关系带来的困难， 通过钢筋混凝土的载荷变形关系， 提出了钢筋混凝土弹塑性损伤本构模型. 该模型假设钢筋混凝土的力学行为由两部分组成， 一是由微裂纹形成的损伤行为， 它具有零屈服强度的刚性完全塑性本构关系； 二是基体行为， 服从不包括软化的弹塑性本构关系. 在加载过程中， 变形的增加使前一种行为转化为后一种行为. 模型包括4个阶段： 线弹性阶段、 混凝土为主体的弹塑性阶段、 钢筋为主体的弹塑性阶段和应变软化阶段. 模型反映了损伤引起了钢筋混凝土应变软化、 剪切刚度降低和诱致各向异性. 采用Willam-Wanke 塑性本构描述混凝土的非线性行为， 其参数标定通过Hsu的软化桁架理论以及Vecchio & Collins的修正压应力理论进行， 考虑了钢筋混凝土中钢筋与混凝土之间的相互作用. 运用此模型分析钢筋混凝土梁的载荷-挠度关系， 并与实验结果相比较， 验证了模型的正确性.

钢筋混凝土； 塑性； 本构； 损伤； 强度

0 引 言

钢筋混凝土(Reinforced Concrete, RC)被广泛应用于工程结构中， 如漂浮容器、 近海平台、 地下掩体、 反应容器和大坝等， 为提高这些构件的设计合理性， 需要考虑RC的力学行为. 由于RC极不均匀， 研究其力学行为需要大的测试样品和测试装置， 才能得出合理的力学模型. 受试验条件的限制， 大尺寸试验需将试件做成一定的结构， 通过研究结构载荷变形之间的关系研究其力学行为. 目前对RC的研究主要集中于梁、 板和壳等结构， 分析其在一维和二维受力下的力学行为[1-2]. 而对于复杂结构则必须考虑三维载荷下的力学行为. 目前对于三维分析的软件已经很多， 但要得到正确的分析结果， 合适的力学模型是必不可少的.

裂纹是RC产生非线性的主要原因[3]， 即使在更高的侧限压力下， 混凝土在加载和卸载阶段刚度减少、 应变软化等行为仍是存在的， 因而纯粹采用弹塑性理论不能充分地描述混凝土的本构[4-5]. Desai等[6-7]对本构模型进行了分级， 以具有关联流动法则的各向同性强化弹塑性模型为基础模型， 考虑到应变软化行为， 用损伤对基础模型进行了修正. Frantziskonis等[8-11]提出了带有应变软化的混凝土模型， 模型中的损伤变量体现了加载过程中卸载刚度的降低、 损伤诱致的各向异性和应变软化行为. 李杰等[12-14]通过分析混凝土的基本损伤机制， 给出了一类基于能量的弹塑性损伤本构， 在基体应力空间确定了塑性变形的演化法则和塑性Helmholtz自由能； 通过分析单轴受拉和受压力学行为， 给出标定后有效应力空间中的模型参数， 对该模型进行数值求解， 并用试验进行了验证. 由于钢筋和混凝土的力学行为差别大， 因而在不同的载荷下， 钢筋和混凝土所产生的不同变形使钢筋和混凝土之间的相互作用差别很大， 导致了RC的复杂力学行为.

RC的力学行为主要由混凝土和钢筋的力学行为以及它们之间的相互作用决定的. 宁建国等[15-17]采用缩比后的试件对RC的力学行为进行了研究， 由于试件尺寸较小， 钢筋的作用没有体现出来， 结果不能反映RC真实的力学行为. Vecchio等[18]对尺寸为890 mm×890 mm×70 mm RC板进行了二维加载试验， 结合力的平衡方程和应变协调条件， 考虑主应力和主应变方向一致， 给出了RC压缩场理论. 随着压缩场理论的运用， Bentz等[19]发现混凝土的压缩软化效应， 提出了修正压缩场理论. Abdeldjelil等[20-21]通过对22块全尺寸RC板进行双轴拉伸和压缩试验， 发现垂直于压缩方向的拉伸应变的存在， 使混凝土压缩强度降低， 引起了混凝土的压缩软化； 通过对17块 RC板进行单轴拉伸试验， 给出混凝土和钢筋相互作用过程中各自的应力-应变关系， 提出了软化桁架理论. 这些研究仅限于二维的分析， 没有考虑损伤对RC性能的影响. Yin等[22-23]将钢纤维和聚丙烯纤维的作用叠加在混凝土上， 给出了钢-聚丙烯混杂纤维混凝土的三维模型， 通过试验标定了模型参数. 此方法将钢-聚丙烯混杂纤维混凝土作为均匀材料， 没有考虑损伤的作用. 由于RC的非均匀性， 提出的模型除要考虑钢筋和混凝土之间相互作用外， 还应考虑裂纹对力学行为的影响.

本文根据大尺寸RC在单轴和双轴受力下的应力-应变曲线特征， 分析了钢筋和混凝土在加载过程中的力学行为变化， 提出了四阶段RC弹塑性损伤本构. 由于裂纹在加载过程中的演化引起RC卸载刚度降低和应变软化行为， 采用Frantziskonis和Desai损伤模型[24]对钢筋和混凝土弹塑性模型进行修正， 提出了RC弹塑性损伤模型. 将所得RC模型运用于梁的非弹性弯曲理论得出梁的载荷-挠度曲线， 并与实验结果对比， 验证了模型的正确性.

1 Frantziskonis和Desai损伤模型

1.1 基本假设

1) 钢筋混凝土的力学行为由两部分组成， 一是由微裂纹形成的损伤行为， 它具有零屈服强度的刚性完全塑性本构关系， 如图1(a)所示； 二是基体行为， 服从弹塑性本构关系， 如图1(b)所示. 将这两部分的力学行为合成为具有应变软化效应的RC弹塑性模型， 如图1(c)所示.

图 1 RC应力-应变关系Fig.1 RC stress- strain relationship

2) RC平均应力等于两部分的应力之和. 损伤行为的剪应力为零， 静水压力由周围基体的静水压力决定， 即损伤行为的应力等于基体的静水压力.

3) 加载过程中的塑性变形导致RC发生损伤， 而卸载过程不发生损伤.

1.2 损伤变量

RC整体的体积为V， 基体的体积为Vt， 损伤部分的体积为V0， 即V=Vt+V0. 基体的体积等于混凝土的体积Vc和钢筋的体积Vs之和， 即Vt=Vc+Vs. 混凝土体积百分比为rc=Vc/V， 钢筋体积百分比为rs=Vs/V. 损伤部分体积比r=V0/V(0≤r≤1)定义为损伤变量， 在损伤发生之前，r=0； 当应力达到残余应力时，r达到最大值，ru≈1. 在此模型中，r作为连续场变量代替体中的离散部分.

1.3 应力和应变

根据假设2)， 应力之间的关系为

根据等效应变原理， 各部分应变相等， 即

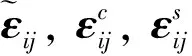
1.4 卸载时剪切模量的降低和损伤诱致的各向异性

对式(2)求微分， 可得应力增量的表达式

1.4.1 卸载时剪切模量的降低

根据假设3)， 卸载时dr=0， 式(4)可转化为

根据虎克定律， 式(5)转化为

当i=1,j=2时，

此式表明卸载时剪切模量与r有关， 随着载荷的增加，r增加， 因而剪切模量降低， 这与钢筋混凝土循环载荷的试验结果是一致的[25].

当j=j=k时， 式(6)转化为

此式表明卸载时体积模量与常数r无关， 静水压力不引起损伤.

1.4.2 损伤诱致的各向异性

根据弹塑性理论的本构关系， 式(4)转化为

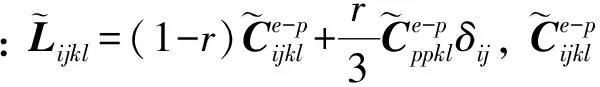
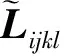
1.5 损伤演化法则

将损伤变量表示为塑性偏应变的函数[10]

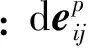
1.6 基体应力和整体应力的关系

基体应力为不考虑损伤时RC的应力， 为了表达方便， 将基体应力视为有效应力. 为了从试验中获得有效应力空间中的模型参数， 需建立有效应力和整体应力之间的关系. 根据式(2)有

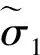
2 基体弹塑性行为

根据RC加载过程中的变形特点， 如图1(c)， 将整个变形过程分为线弹性阶段、 混凝土为主体的弹塑性阶段、 钢筋为主体的弹塑性阶段和应变软化阶段[26]. 分界点分别为混凝土开裂点、 裂缝处钢筋屈服点和钢筋完全屈服点. 应变软化阶段是由钢筋完全屈服以后的力学行为和损伤叠加而成， 基体弹塑性行为由混凝土和钢筋的弹塑性本构组成， 主要包括前3个阶段， 如图1(a).

2.1 线弹性阶段

混凝土在低应力时几乎不发生损伤[28]， 损伤参数r=0，rc=rs=常数. 在RC开裂之前， 混凝土和钢筋处于弹性状态， 应力-应变呈线性关系， 整体力学行为由钢筋和混凝土的弹性行为叠加而成， 增量本构关系如下

对于三维受力的混凝土， 应力-应变关系为

其中：

钢筋经常作为一维受力单元， 在i方向的应力-应变关系为

其中：

2.2 混凝土为主体的弹塑性阶段

当混凝土开裂后， 损伤开始， 刚度突然降低， 随着钢筋和混凝土之间的相互作用增加， 混凝土发生拉伸强化， 刚度逐渐增加. 此阶段钢筋处于弹性状态， 混凝土发生塑性变形， 基体的塑性由混凝土的塑性决定. 采用Willam-Warnke五参数模型和Drucker-Prager 型塑性势函数[29-31]分析混凝土弹塑性行为， 以混凝土开裂作为屈服点， 以裂缝处的钢筋屈服为混凝土的破坏点， 根据均匀强化特征， 得出混凝土应力-应变之间的增量关系. 钢筋应力-应变之间的增量关系通过钢筋的弹性模量表示.

2.2.1 混凝土加载面

五参数破坏模型在坐标系ρ,ξ和θ下的表达式为[16]

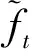
2.2.2 混凝土有效拉伸和压缩强度

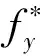
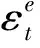
混凝土发生压缩软化， 软化因子β为[20]

式中：ε1为RC中混凝土达到压缩强度时对应的拉伸主应变，ε0为混凝土标准强度时所对应的应变， 在无侧限压力时， 一般取ε1=νε0，ν为泊松比. 发生压缩软化的混凝土达到压缩强度时对应的应变为βε0[18]， 对应的塑性应变为

将式(17)和式(20)的拉压塑性应变代入式(10)， 得出混凝土拉伸强度和压缩强度对应的损伤变量值rt和rc. 由式(12)给出混凝土有效拉伸和压缩强度为

2.2.3 流动法则

采用Drucker-Prager函数作为塑性势函数[29-31]

流动法则表示为

式中：α为反映混凝土材料体积膨胀的系数， 由式(8)可知与损伤无关，α由试验确定， 一般取为0.2～0.3， 建议模型中取为0.2[14].

2.2.4 强化法则

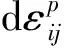
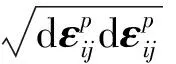
强化函数通过RC板的单轴拉伸试验得出， 混凝土在此阶段平均应力σr和平均应变εr之间的关系[11]

将混凝土平均应力和拉伸强度用有效值代替， 得到有效强化函数的表达式为

强化函数通常表示为率的形式， 对式(27)求微分

2.2.5 弹塑性本构方程

根据弹塑性理论， 总的应变增量等于弹性应变增量和塑性应变增量的和， 即

根据虎克定律， 应力增量的表达式为

根据一致性条件

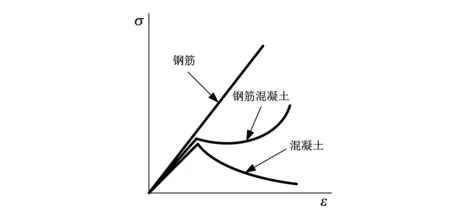
图 2 RC力学行为的分解Fig.2 Decomposition of RC behavior

将式(23)和式(31)式代入式(32)， 可得dλ的表达式为

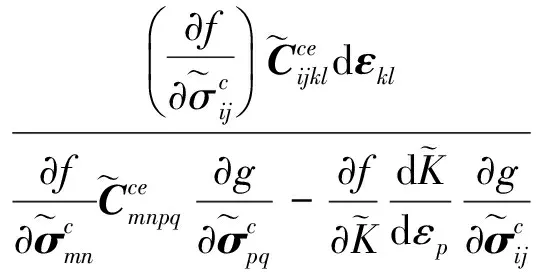
将式(33)代入式(31)中， 可得混凝土在有效应力空间中的增量应力-应变关系

钢筋有效增量应力-应变关系为

将式(34)和式(35)按照式(13)叠加起来， 即为此阶段RC的有效应力-应变增量关系. 图1(a)中给出了此阶段RC应力-应变曲线向下凹， 这从图2中钢筋和混凝土力学行为的叠加能够得到.

2.3 钢筋为主体的弹塑性阶段和应变软化阶段

裸露钢筋屈服时， 即混凝土达到式(16)的拉伸强度， 第三阶段开始， 裂缝处的钢筋进入强化阶段， 钢筋和混凝土之间的关系更为复杂. 此时钢筋应变大大增加， 混凝土的应力非常小. 实验表明当裂缝处钢筋屈服时， 95%以上的拉应力被钢筋所承担， 此阶段基体的力学行为由钢筋的受力性质决定. 为了简单起见， 此处采用一维分析. RC中钢筋的平均应力应变关系为[21]

式中：fs为钢筋的平均应力；εs为钢筋的平均应变；Es为钢筋有效弹性模量；Ep为钢筋强化部分的斜率， 一般为(1.8%～2.5%)Es；f0=0.89fy,fn=0.91fy.

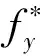
用式(38)中钢筋的应变减去式(39)中的弹性应变， 得到钢筋的塑性应变. 将塑性应变代入式(10)， 得出此阶段的损伤变量值.

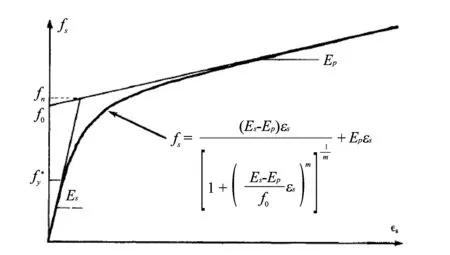
图 3 钢筋平均应力-应变曲线[21]Fig.3 Stress-strain relationship of steel[21]

3 模型初步验证

3.1 实 验

采用液压伺服试验机对6种尺寸为1 800 mm×120 mm×120 mm 的RC简支梁进行三点弯实验， 如图 4 所示. 梁的总长为1 800 mm， 跨度为1 200 mm， 钢筋在试件截面均匀分布， 纵筋分3排排列， 间距44 mm， 每排2个， 间距为80 mm， 如图 5 所示.

图 4 三点弯实验Fig.4 The three-point bending test of beam

图 5 RC梁的结构和尺寸Fig.5 Details of beam

3.2 模型计算

表 1 给出了模型计算所需钢筋和混凝土的弹性、 塑性和损伤参数. 其中混凝土损伤参数k,R和ru为侧限压力、 初始密度、 尺寸率的函数， 与混凝土强度相关性不大[32-33]. 决定损伤参数最好的方法是通过试验获得， 如X光、 超声波透视等技术测出裂缝传播的真实情况， 由于试验操作起来比较困难， 此处参数直接通过混凝土应力-应变曲线进行预测. 由于本文中RC梁以上相关因素基本相同， C27和C40都属于普通强度的混凝土， 其应变软化阶段曲线形状基本一致， 为了简化起见， 表1中采用相同的损伤参数[28]. 将上述的模型运用于梁的非弹性弯曲理论， 得出梁的载荷-挠度关系， 求解步骤如下：

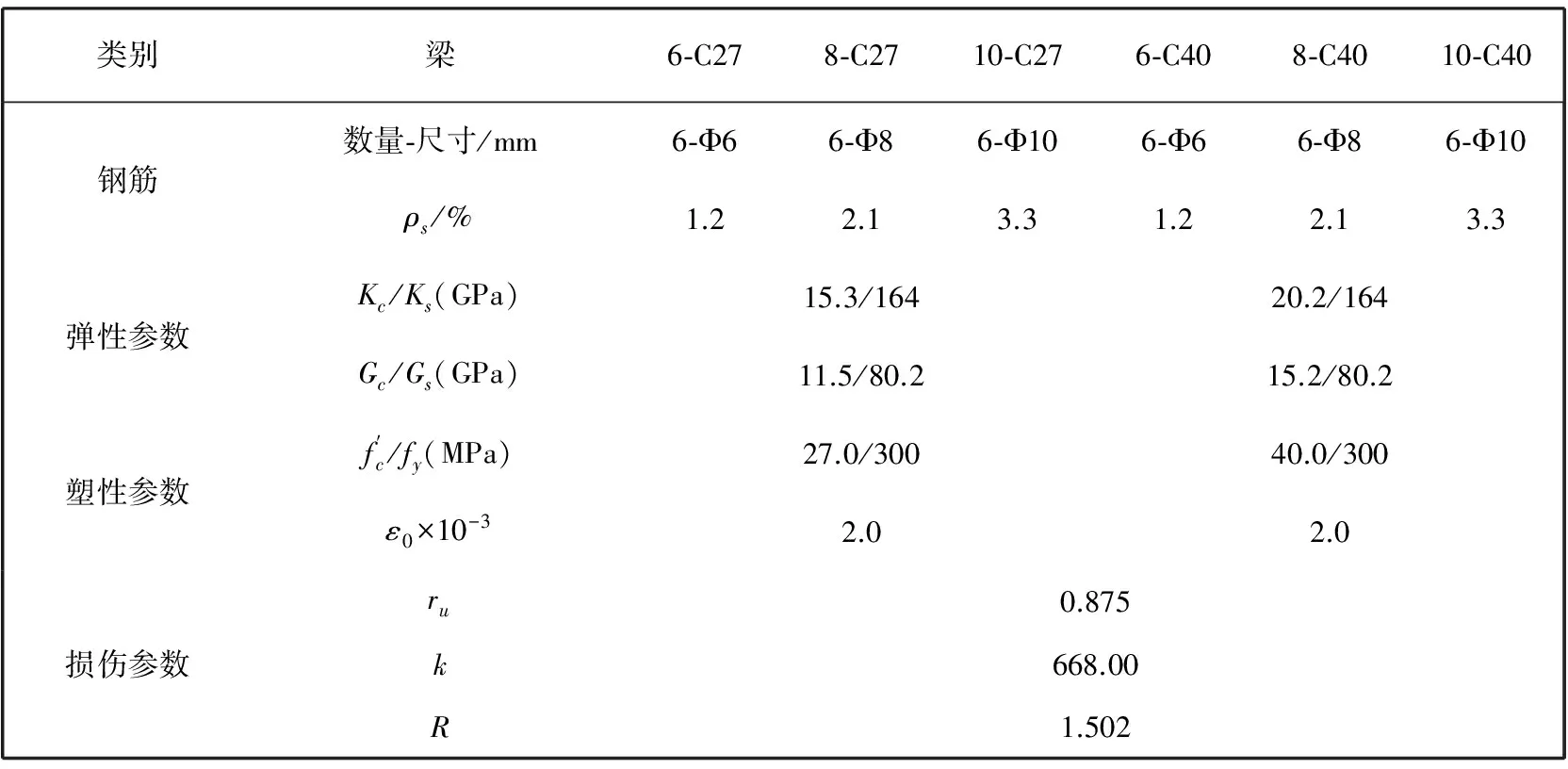
表 1 梁中混凝土和钢筋的特征

① 已知混凝土的开裂应变， 根据式(13)得出RC第一阶段的应力-应变直线关系.

② 当应力达到混凝土的开裂应力时， 第二阶段开始. 给出应变增量dε1， 代入式(34)和式(35)得出混凝土和钢筋基体应力增量； 将两者按照式(13)叠加起来， 得出基体的应力增量； 根据式(31)和式(30)得出混凝土塑性应变增量， 根据式(10)求出损伤值； 将基体的应力增量和损伤值代入式(4)求出RC此阶段整体应力增量.

③ 按照步骤②反复计算， 得出第二阶段的应力-应变曲线. 当混凝土整体应力达到方程式(16)给出的裸露钢筋屈服时所对应的平均应力时， 变形进入第三阶段.

④ 给定应变增量， 根据式(38)得出基体应力增量， 根据式(39)得出弹性应变； 给定的应变增量减去弹性应变增量， 得出塑性应变增量； 根据式(10)求出损伤值， 代入式(4)得出钢筋的应力增量.

⑤ 按照步骤④进行反复计算， 直至r=ru， 运算停止， 得出第三、 四阶段的应力应变曲线.

⑥ 根据前5步得出RC应力应变关系， 已知梁跨中作用载荷P， 根据非弹性弯曲梁的理论

得出曲率半径β， 代入下式

得出梁中间的挠度δ. 式中：b为截面的宽度，h为高度，y为微元离中性轴的距离，ε′为梁截面上下侧的应变，l为梁的长度，x为某截面离简支约束的距离.

3.3 试验与模型计算结果的对比和讨论

图 6 给出了梁载荷-挠度的模型计算结果与试验值， 从图中可以看出， 模型计算值大于试验值， 但曲线的形状和实验点的趋势是一致的. 曲线的形状反映了RC非线性本构关系.

第一阶段为线弹性阶段， 钢筋和混凝土都发生弹性变形. 此时的弹性应变较小(小于混凝土开裂应变0.000 08)， 钢筋的作用不明显， 规范中常常将混凝土的压缩弹性模量等效为RC抗弯刚度中的弹性模量.

第二阶段为被钢筋强化的混凝土塑性变形和钢筋的弹性变形叠加形成的下凹曲线. 从图中可以看出， 配筋率越高时上升段的下凹越不明显. 这是由于此阶段混凝土发生塑性变形， 钢筋仍处于弹性状态. 混凝土由于钢筋的作用进入应变软化阶段， RC的力学行为如图2所示. 由于混凝土的承载能力降低， 配筋率对RC梁的变形影响变大, 曲线的凹度随配筋率的增加而减小. 凹度反应了结构的弯曲刚度， 此模型主要用于发生弯曲变形的RC结构上.

第三、 四阶段钢筋发生塑性变形， 塑性应变增大， 损伤值增大， 混凝土作用逐渐消失. RC的力学行为主要由钢筋的塑性和损伤行为组成， 随着钢筋刚度的降低和损伤的增加， 形成了曲线的上凸部分和最后的下降部分.

图 6 RC梁载荷-挠度实验值和模型预测结果的对比Fig.6 Comparison of proposed model and experimental results on load-deflection relationships of RC beams

4 结 论

本文基于大尺寸RC的试验结果， 结合前人给出的混凝土应变软化模型， 提出了一种基于损伤的RC弹塑性本构模型. 该模型将RC本构分为4个阶段： 线弹性阶段、 混凝土为主体的弹塑性阶段、 钢筋为主体的弹塑性阶段和应变软化阶段.

第一阶段采用线弹性理论， 将钢筋和混凝土的受力叠加起来. 第二阶段采用三维混凝土塑性理论， 其参数标定通过Abdeldjelil & Hsu的软化桁架理论以及Vecchio & Collins的修正压应力理论进行， 考虑了钢筋与混凝土之间的相互作用. 此阶段的混凝土的应力随着应变的增大而降低， 与钢筋的弹性应力-应变关系叠加， 体现了RC此阶段应力-应变曲线下凹的特点. 第三、 四阶段模型通过Hsu给出的钢筋平均应力和平均应变之间的关系进行， 其中考虑到钢筋和混凝土相互作用. 将此种弹塑性关系与损伤部分相结合， 体现了第三阶段RC应力-应变曲线上凸和第四阶段应变软化的特点.

将提出的模型初步运用于三点弯RC梁的结构分析， 根据非弹性弯曲梁理论， 得出梁的载荷挠度关系， 与实验结果吻合.

[1] 蔡松柏， 沈蒲生. 一种高阶非线性钢筋混凝土平板单元[J]. 力学学报， 1998， 30(3)： 379-384.

Cai Songbai， Shen Pusheng. A higher order nonlinear FEM for RC plates[J]. Chinese Journal of Theoretical and Applied Mechanics， 1998， 30(3)： 379-384. (in Chinese)

[2] 谢靖中， 江欢成. 钢筋混凝土梁的非线性均质材料本构等效[J]. 工程力学， 2001(A02)： 44-49.

Xie Jingzhong， Jiang Huancheng. The equivalent constitutive relationship of the nonlinear homogeneity material on reinforced concrete beams[J]. Engineering Mechanics， 2001(A02)： 44-49. (in Chinese)

[3] 杜修力， 张建伟， 符佳， 等. 钢筋混凝土构件的尺寸效应研究进展及展望[J]. 建筑科学与工程学报， 2009， 26(3)： 14-19.

Du Xiuli， Zhang Jianwei， Fu Jia， et al. Research progress and prospect of size on reinforced concrete members[J]. Journal of Architecture and Civil Engineering， 2009， 26(3)： 14-19. (in Chinese)

[4] Papanikolaou V K， Kappos A J. Cofinement-sensitive plasticity constitutive model for concrete in triaxial compression[J]. International Journal of Solids and Structures， 2007， 44(21)： 7021-7048.

[5] Bazant Z P， Belytschko T B， Chang T P. Continuum theory for strain-softening[J]. Journal of Engineering Mechanics， 1984， 110(12)： 1666-1692.

[6] Desai C S， Somasundaram S， Frantziskonis G. A hierarchical approach for constitutive modelling of geologic materials[J]. International Journal for Numerical and Analytical Methods in Geomechanics， 1986， 10(3)： 225-257.

[7] Desai C S. Mechanics of materials and interfaces： The disturbed state concept[M]. Boca Raton: CRC Press， 2000.

[8] Frantziskonis G， Desai C S. Constitutive model with strain softening[J]. International Journal of Solids and Structures， 1987， 23(6)： 733-750.

[9] Frantziskonis G， Desai C S. Elastoplastic model with damage for strain softening geomaterials[J]. Acta Mechanica， 1987， 68(3-4)： 151-170.

[10] Frantziskonis G， Desai C S. Analysis of a strain softening constitutive model[J]. International Journal of Solids and Structures， 1987， 23(6)： 751-767.

[11] Frantziskonis G. Progressive damage and constitutive behavior of geomaterials including analysis and implementation[D]. Arizona： The University of Arizona， 1986.

[12] 李杰， 吴建营. 混凝土弹塑性损伤本构模型研究I： 基本公式[J]. 土木工程学报， 2005， 38(9)： 14-20.

Li Jie， Wu Jianying. Elastoplastic damage constitutive model for concrete based on damage energy release rates， part I： basic formulations[J]. China Civil Engineering Journal， 2005， 38(9)： 14-20. (in Chinese)

[13] 李杰， 吴建营. 混凝土弹塑性损伤本构模型研究II： 数值计算和试验验证[J]. 土木工程学报， 2005， 38(9)： 21-27.

Li Jie， Wu Jianying. Elastoplastic damage constitutive model for concrete based on damage energy release rates， part II： numerical algorithm and verifications[J]. China Civil Engineering Journal， 2005， 38(9)： 21-27. (in Chinese)

[14] 李杰， 任晓丹， 黄桥平. 混凝土粘塑性动力损伤本构关系[J]. 力学学报， 2011， 43(1)： 193-201

Li Jie， Ren Xiaodan， Huang Qiaoping. A viscoplastic damage constitutive model for concrete[J]. Chinese Journal of Theoretical and Applied Mechanics， 2011， 43(1)： 193-201. (in Chinese)

[15] 宁建国， 商霖， 孙远翔. 混凝土材料冲击特性的研究[J]. 力学学报， 2006， 38(2)： 199-208.

Ning Jianguo， Shang Lin， Sun Yuanxiang. Investigation on impact behavior of concrete[J]. Chinese Journal of Theoretical and Applied Mechanics， 2006， 38 (2)： 199-208. (in Chinese)

[16] Liu H F， Ning J G. Mechanical behavior of reinforced concrete subjected to impact loading[J]. Mechanics of Materials， 2009， 41(12)： 1298-1308.

[17] 商霖. 钢筋混凝土材料动态本构特性及其破坏行为的研究[D]. 北京： 北京理工大学， 2005.

[18] Vecchio F J. The response of reinforced concrete to in-plane shear and normal stresses[D]. Toronto： University of Toronto， 1982.

[19] Bentz E C， Vecchio F J， Collins M P. Simplified modified compression field theory for calculating shear strength of reinforced concrete elements[J]. ACI Structural Journal， 2006， 103(65)： 614-624.

[20] Abdeldjelil B， Hsu T T C. Constitutive laws of softened concrete in biaxial tension-compression[J]. ACI Structure Journal， 1995， 92(5)： 562-573.

[21] Abdeldjelil B， Hsu T T C. Constitutive laws of concrete in tension and reinforcing bars stiffened by concrete[J]. ACI Structure Journal， 1994， 91(4)： 465-474.

[22] Yin C. Plasticity model for hybrid-fiber-reinforced concrete under true triaxial compression[J]. Journal of Engineering Mechanics， 2014， 140： 393-405.

[23] Yin C. Constitutive modeling of steel-polypropylene hybrid fiber reinforced concrete using a non-associated plasticity and its numerical implementation[J]. Composite Structure， 2014， 111： 497-509.

[24] 谢和平. 岩石混凝土损伤力学[M]. 徐州： 中国矿业大学出版社， 1990.

[25] Irawan P， Maekawa K. Path-dependent non-linear analysis of reinforced concrete shells[J]. Journal of Materials， Concrete Structures and Pavements， 1997， 34(557)： 121-134.

[26] Chen W F. Plasticity in reinforced concrete[M]. New York: J. Ross Publishing， 2007.

[27] Frantziskonis G. Distributed damage in composites， theory and verification[J]. Composite structures， 1988， 10(2)： 165-184.

[28] Jan G M, Van M. Strain softening of concrete under multiaxial loading conditions[D]. Netherlands： Eindhoven University of Technology， 1984.

[29] Chen W F， Han D J. Plasticity for structural engineers[M]. Fort Vince: Springer Science & Business Media， 2012.

[30] Chen W F， Zhang H. Theory， problems， and CAE softwares of structural plasticity[M]. New York: Springer-Verlag， 1988.

[31] 殷有泉， 曲圣年. 弹塑性耦合和广义正交法则[J]. 力学学报， 1982， 18(1)： 63-70.

Yin Youquan， Qu Shengnian. Elastoplastic coupling and generalized normality rule[J]. Chinese Journal of Theoretical and Applied Mechanics. 1982， 18(1)： 63-70. (in Chinese)

[32] Vecchio F J， Collins M P. Compression response of cracked reinforced concrete[J]. Journal of Structure Engineering， 1993， 119(12)： 3590-3610.

[33] Jansen D C， Shah S P. Effect of length on compressive strain softening of concrete[J]. Journal of Engineering Mechanics， 1997， 123(1)： 25-35.

[34] Van Mier J G M， Shah S P， Arnaud M， et al. Strain-softening of concrete in uniaxial compression[J]. Materials and Structures， 1997， 30(4)： 195-209.

ElastoplasticModelwithDamageforReinforcedConcrete

ZHAN Ting-bian1, NING Jian-guo2, WANG Zhi-hua3, REN Hui-lan2

(1. College of Mechanical and Electrical Engineering, North University of China, Taiyuan 030051, China； 2. State Key Laboratory of Explosion Science and Technology, Beijing Institute of Technology, Beijing 100081, China； 3. Shanxi Key Laboratory of Material Strength and Structure Impact, Taiyuan University of Technology, Taiyuan 030024, China)

During the loading process, stress and strain are inhomogeneous in the reinforced concrete, so it is difficult to determine the constitutive relation from the tests. In order to ignore the difficulties in identifying the influence of such nonhomogeneities, an elastoplastic model with damage for reinforced concrete is proposed by the observed load-deformation relations in this paper. It is assumed that behaviour of reinforced concrete element is decomposed in two parts. In the first part, which refers to the damaged part, the behaviour is depicted as rigid, perfectly plastic with zero yield strength. The second part, representing topical behaviour, is non-softening and obeys an elastoplastic constitutive law. During the loading process, topical behaviour is “transformed” to damaged one. The model is divided into four intervals: the elastic stage, the based elastoplastic stage on concrete, the based elastoplastic stage on reinforcement and the strain softening stage. The damage variable is responsible for the softening in strength, for the degradation of the elastic shear modulus, and for induced anisotropy. The parameters of rebar and concrete are calibrated by the softened truss mod proposed by Abdeldjelil & Hsu and the modified compression field theory proposed by Vecchio & Collins, considering the interaction between the concrete and reinforcement. The model is applied to analyze the load-deflection relationships of RC beams and shows very good agreement with the experimental results.

reinforced concrete; plasticity; constitutive relation; damage; strength

1673-3193(2017)03-0380-11

2016-10-24

国家自然科学基金资助项目(11390362)； 山西省青年科技研究基金资助项目(201601D202005)； 中北大学2016年校科研基金资助项目

展婷变(1979-)， 女， 讲师， 主要从事钢筋混凝土力学行为的研究.

O347

A

10.3969/j.issn.1673-3193.2017.03.022

声明

本刊已许可中国学术期刊(光盘版)电子杂志社在中国知网及其系列数据库产品中，以数字化方式复制、汇编、发行、信息网络传播本刊全文。该社著作权使用费与本刊稿酬一并支付。作者向本刊提交文章发表的行为即视为同意我编辑部上述声明。