绞刀运动姿态的欧拉角表示
苏召斌,林 森
(中交天津港航勘察设计研究院有限公司,天津 300457)
绞刀运动姿态的欧拉角表示
苏召斌,林 森
(中交天津港航勘察设计研究院有限公司,天津 300457)
传统的绞刀运动往往被简化为横移加旋转的二维运动方式,这种运动简化方法难以准确地定义绞刀的位置和姿态。以刚体运动学为出发点,严格推导了绞刀运动的欧拉表示方法,以全新的视角描述了绞刀的运动。对绕任意轴转动的欧拉旋转进行了公式推导,能够简单而准确地描述绞刀的位置和姿态变化。使用绞刀横移偏转角度、下放角度和旋转角度定义绞刀的位置和姿态,并给出了绞刀和刀齿位置姿态的表达形式。
绞刀;欧拉角;坐标变换
0 引言
在港口建设、航道疏浚及吹填工程中,绞吸式挖泥船被广泛应用[1],绞刀是绞吸式挖泥船的核心装备。绞吸挖泥船在估算挖泥产量时,将被挖泥土看成切层厚度、步进距离和摆宽的乘积,切层厚度指绞刀切削块的竖向尺寸,步进距离指切削块的纵向尺寸,摆宽就是指切削区间的横向尺寸。事实上,绞刀的运动是三种转动的叠加,分别为绕着定位钢桩的转动、绕着桥架耳轴的转动和绞刀轴线的转动[2]。绞刀距离定位钢桩约为100 m,距离绞刀耳轴约40 m,而绞刀直径仅仅约为3 m,经过简化以后,普遍将绞刀运动分解为沿着水平方向的平动和沿着绞刀轴线的转动[3]。在绞吸挖泥船施工的一个摆宽区间,绞刀绕着定位钢桩的摆动幅度将近,目前对绞刀的运动简化与实际工作状态并不相符。
目前,描述空间结构姿态表示的有PRY角、欧拉角和四元数等,其中欧拉角是用来描述转动刚体的3个独立角参量,描述绞刀的运动更适合[4-6]。
1 坐标变换
1.1 绞刀运动分析
绞刀整体运动一般被看做横移和转动的复合运动,其中绞刀距离钢桩轴线的距离远大于绞刀的直径,绕钢桩的旋转运动被简化为横移运动。如图1所示,当绞吸挖泥船向前推移一个步进距离,绞刀进入下一个往复运动过程。在每一个往复运动过程中,钢桩均是在固定位置。如图2所示,除了绕钢桩转动外,绞刀的运动还包括:绕桥架耳轴的旋转运动和绕绞刀轴线的旋转运动。因此,绞刀的运动是上述三种转动的复合运动。
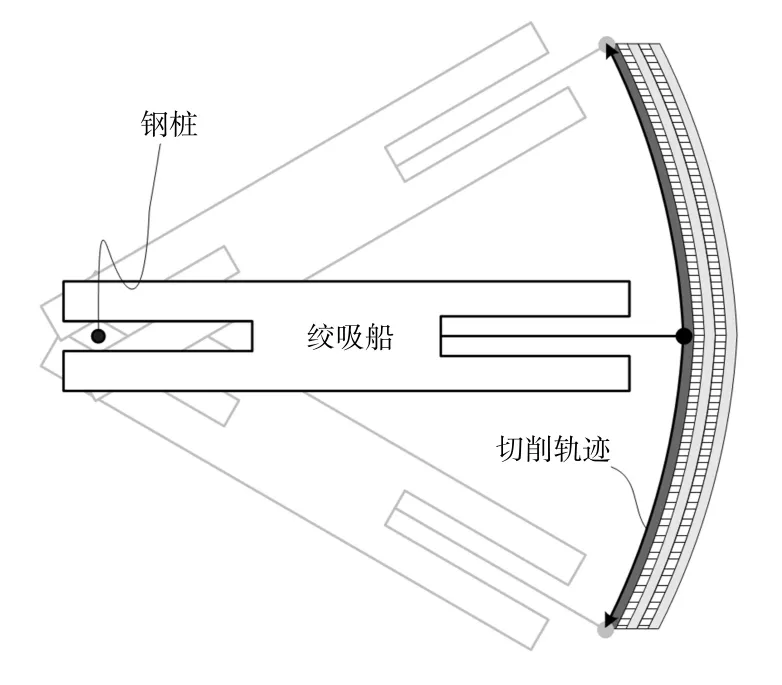
图1 绞刀绕钢桩运动示意图Fig.1 Diagrammatic sketch of the cutter rotated around the steel pile
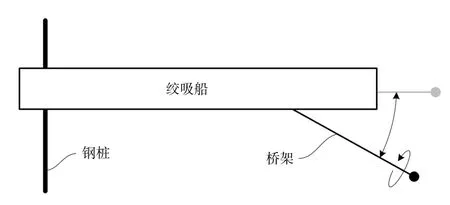
图2 绞刀绕桥架耳轴转动示意图Fig.2 Diagrammatic sketch of the cutter rotated around the bridge trunnion
1.2 三维坐标变换
刚体的运动可以等效为一次平动和一次转动。刚体上的任意一点P在固定坐标系A中的齐次坐标为AP=(xA,yA,zA,1),在坐标B系中的齐次坐标为BP=(xB,yB,zB,1),则存在关系式:

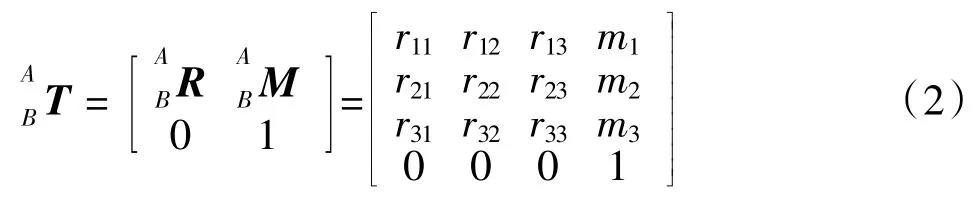

式中:绕x轴旋转的矩阵为Rx(琢);绕y轴旋转的矩阵为Ry(茁);绕z轴旋转的矩阵为Rz(酌)。对于右手坐标系逆时针为正,即绕x轴旋转时,由y轴转向z轴为正;绕y轴旋转时,由z轴转向x轴为正;绕z轴旋转时,由x轴转向y轴为正。
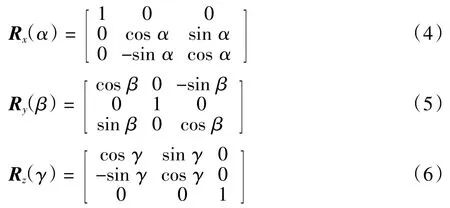

1.3 定点旋转的欧拉变换
欧拉角是用来唯一地确定定点转动物体位置的3个一组独立参量,由章动角兹,进动角鬃和自转角渍组成。按照旋转所绕轴次序的不同,共有12种不同的欧拉角,6种对称型欧拉角为:XYX,XZX,YXY,YZY,ZXZ和 ZYZ。6种非对称型欧拉角为:XYZ、XZY、YXZ、YZX、ZXY和ZYX。
如图3所示的ZXZ型欧拉角,即坐标轴先绕z轴旋转鬃角,再绕新的x轴(即N轴)旋转兹角,最后绕新的z轴(即z忆轴)旋转渍角,刚体旋转矩阵表示为:

同理,其它5种对称型欧拉角对应的旋转矩阵可以按照旋转的先后顺序求解。
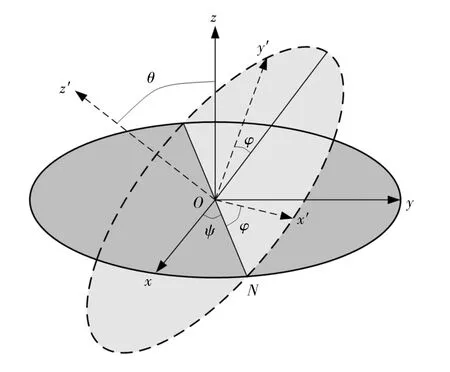
图3 定点转动的欧拉角示意图Fig.3 Diagrammatic sketch of Euler angle rotated round the fixed point
当欧拉角类型为ZXY时,即坐标轴先绕y轴旋转鬃角,再绕新的x轴旋转兹角,最后绕新的z轴旋转渍角,刚体旋转矩阵为:

同理,其它5种非对称型欧拉角对应的旋转矩阵可以按照旋转的先后顺序求解。
1.4 绕任意轴转动的欧拉变换
记固定坐标系为o-xyz,空间物体绕任意轴转动的可以按照如下步骤进行:
1)将轴线平移到坐标原点寅2)将轴线绕固定坐标系的x轴旋转琢角至xoz平面寅3)将轴线绕固定坐标系的y轴旋转茁角至z轴寅4)绕固定坐标系的z轴旋转兹角度寅5)将轴线绕固定坐标系的x轴旋转-茁角至xoz平面寅6)将轴线绕固定坐标系的x轴旋转-琢角至xoz平面寅7)将轴线平移到原位置。
则空间物体绕任意轴的欧拉变换可以看做一系列的旋转变换,按照式(12)进行变换:
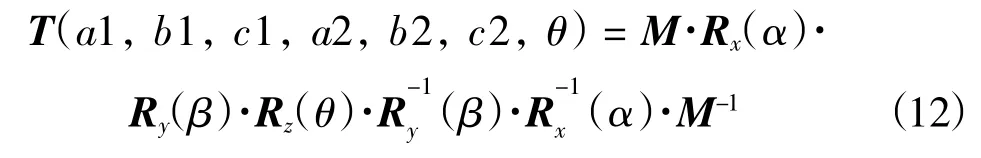
式中:T(a1,b1,c1,a2,b2,c2,兹)为旋转变换矩阵,旋转轴线用起点 p1(a1,b1,c1)和 p2(a2,b2,c2)终点来表示;兹为旋转角度。轴线的方向可以表示为(a,b,c):

同理,步骤3)为轴线绕y轴顺时针旋转-茁角度的变换:
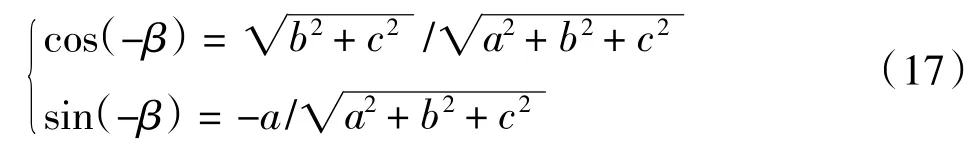
其变换矩阵为:
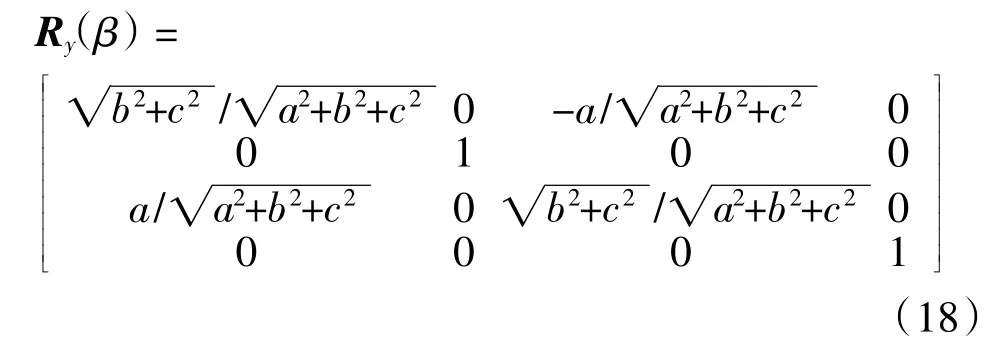
步骤4)的变换矩阵参照式(6),步骤5)的变换矩阵为式(18)逆矩阵,步骤6)的变换矩阵为式(16)逆矩阵,步骤7)的变换矩阵为式(14)逆矩阵,则把上述7个矩阵顺次连乘就是绕任意轴的欧拉变换矩阵:
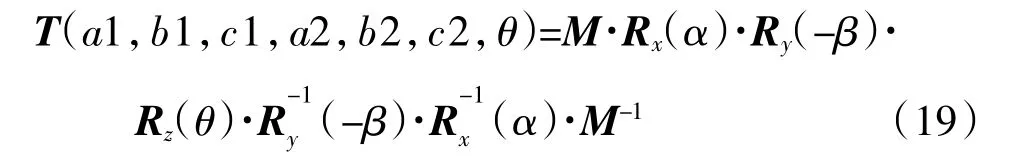
2 绞刀的运动
2.1 坐标系建立
以绞刀抬出水面并且绞刀轴指向船艏方向为基准状态,建立固定参考系M。其中以绞刀轴为z轴并以指向轮毂方向为正,以大圈下平面为xoy平面。同时,建立随动坐标系N,则绞刀在基准状态时,坐标系N和坐标系M重合,相对于船体而言,x轴朝右,y轴朝下,z轴朝前,如图4所示。

图4 绞吸挖泥船Fig.4 Cutter suction dredger
2.2 绞刀姿态确定
绞吸挖泥船施工时,绞刀首先被下放到一定深度处,然后绕着钢桩水平摆动,同时绞刀也绕自身轴线转动。为了表述方便,记绞吸挖泥船横向摆动的偏转角为鬃,一般在正负60毅之间;绞刀的下放角兹,一般小于50毅;绞刀的转动角度为渍,可取任意角度。
绞刀的运动表示方式和欧拉角次序有关。绞刀在施工时,绞刀刀齿分别绕着钢桩轴线、耳轴轴线和绞刀轴线运动。其中钢桩轴线的优先级最高,耳轴轴线次之,绞刀轴线最低,因此欧拉角的次序ZXY。只要给定具体的鬃、兹和渍的大小,就可以按照式(11)确定绞刀的姿态。
2.3 绞刀位置确定
记钢桩轴线到耳轴轴线的距离为A,耳轴轴线到参考系M的距离为B,则位置矩阵为
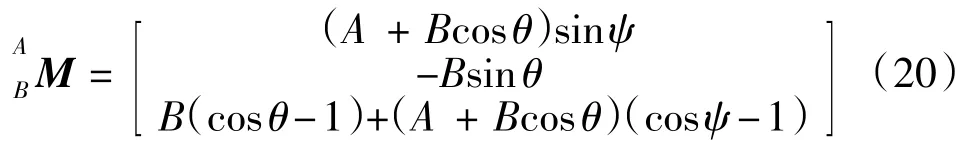
综上所述,绞刀的运动位置和姿态可以描述为:
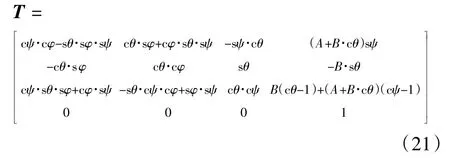
式中:s兹表示 sin兹;c兹表示 cos兹;s鬃 表示 sin鬃;c鬃 表示 cos鬃;s渍 表示 sin渍;c渍 表示 cos渍。
同理,记任意刀齿初始时刻的柱坐标为(R,准,z),则刀齿的位置和姿态可以描述为:
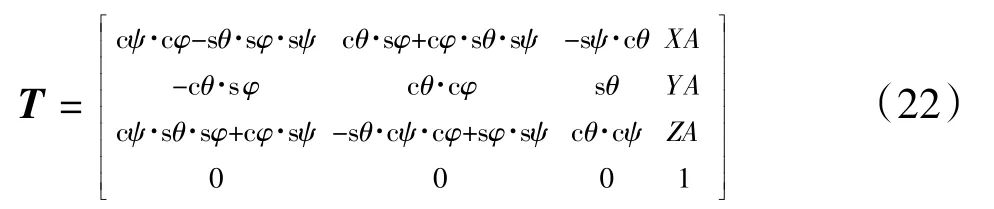
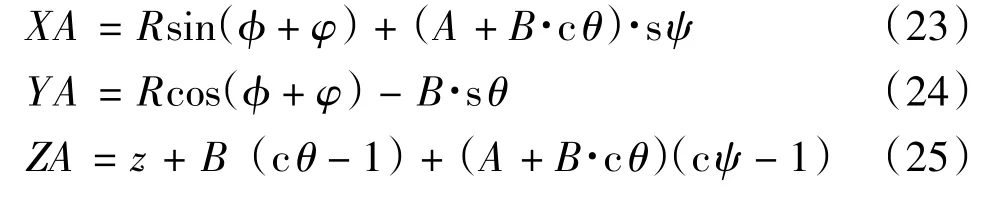
式中:XA是转动后刀齿在固定参考系M下的X坐标;YA是转动后刀齿在固定参考系M下的Y坐标;ZA是转动后刀齿在固定参考系M下的Z坐标。
2.4 实例验证
假设 A=70,B=30,欧拉角为(10,-30,90),即绞刀向右偏转10毅,下放绞刀20毅,转动90毅,记绞刀上的刀齿柱坐标为(1.5,20,0),笛卡尔坐标为(1.410,0.513,0),绞刀大圈中心的坐标为(0,0,0),将各参数带入式(22)中,则偏转后绞刀大圈中心的笛卡尔坐标为(16.667,15.000,-5.477),该刀齿新的笛卡尔坐标为(18.076,14.487,-5.477)。
3 结语
1)以刚体运动学为出发点,讨论了在直角坐标系中的欧拉坐标变换方程。对于绞刀运动描述而言,该方法比传统的横移加旋转的轮摆式运动方式更加准确。
2)推导出绕任意轴的欧拉角旋转方程,利用绞刀钢桩-耳轴-绞刀轴的先后绕转次序,推导出绞刀姿态和位置的关系表达形式。
3)根据旋转次序和旋转方向的不同,利用欧拉坐标变换方法描述了绞刀刀齿的运动轨迹,给出了任意刀齿在任意欧拉角时的位置和姿态表达形式。
在给定绞刀的下放角度、转动偏角和绞刀自转角度时,能够唯一确定绞刀的位置和姿态,同时也能确定每一个刀齿的位置。在后续的研究中,对轨迹方程进行时间求导,能够得出各刀齿的速度,进而求出各刀齿的运动加速度,能够为绞刀的优化设计提供技术支持。
[1] 冯永军,陈新权,丁金鸿,等.绞吸挖泥船桥架发展概述[J].中国港湾建设,2015(8):1-5.FENG Yong-jun,CHEN Xin-quan,DING Jin-hong,et al.Development overview of bridge ladder on cutter suction dredgers[J].China Harbour Engineering,2015(8):1-5.
[2] 李金贵,李进军,杨建华,等.污染底泥精确疏浚技术[J].中国港湾建设,2004(6):11-14,20.LI Jin-gui,LI Jin-jun,YANG Jian-hua,et al.Technology for accurate dredging of contaminated subsoil[J].China Harbour Engi原neering,2004(6):11-14,20.
[3]王翰涛,鲁力群,王秀景.绞吸式挖泥船绞刀系统技术现状及发展[J].机电设备,2014(6):10-16.WANG Han-tao,LU Li-qun,WANG Xiu-jing.Technology status and development of cutter system of cutter suction dredger[J].Mechanical and Electrical Equipment,2014(6):10-16.
[4]张帆,曹喜滨,邹经湘.一种新的全角度四元数与欧拉角的转换算法[J].南京理工大学学报,2002,26(4):376-380.ZHANG Fan,CAO Xi-bin,ZOU Jing-xiang.A new large-scale transformation algorithm of quaternion to Euler angle[J].Journal of Nanjing University of Science and Technology,2002,26(4):376-380.
[5] 林积昶,韩国柱,吴松,等.基于虚拟维修系统的配件模型实时移动方法[J].计算机工程,2010,36(10):254-255.LIN Ji-chang,HAN Guo-zhu,WU Song,et al.Real-time move method for accessory model based on virtual maintenance system[J].Computer Engineering,2010,36(10):254-255.
[6] 徐旭松,杨将新,曹衍龙,等.基于齐次坐标变换的制造误差建模研究[J].浙江大学学报:工学版,2008,42(6):1 021-1 026.XU Xu-song,YANG Jiang-xin,CAO Yan-long,et al.Manufactur原ing error modeling based on homogeneous transformation[J].Journal of Zhejiang University:Engineering Science,2008,42(6):1 021-1 026.
Expression of the moving orientation of cutter by Euler angle
SU Zhao-bin,LIN Sen
(CCCC Tianjin Port&Waterway Prospection&Design Research Institute Co.,Ltd.,Tianjin 300457,China)
The traditional sports of cutter is often simplified as two-dimensional motion with transverse and rotation,this simplified method can not accurately define the movement and posture of cutter.As the starting point of the rigid body kinematics,we rigorously derived the Euler expression of cutter movement,and described the movement of the cutter from a new perspective.We deduced the Euler rotation to any axis,and can describe the position and attitude of the cutter simply and effectively.Uses the sliding angle,downward angle and revolving angle can define cutter position and attitude,and gives the expression of the position and attitude of cutter and tooth.
cutter;Euler angle;coordinate transformation
U615.351
A
2095-7874(2017)12-0062-05
10.7640/zggwjs201712014
2017-05-17
2017-07-13
苏召斌(1986— ),男,山东鄄城人,硕士,工程师,固体力学专业,主要从事疏浚挖泥机具研究和岩土切削数值模拟工作。E-mail:suprc@163.com

