检视高考数学第一轮复习——以排列组合复习为例

伍春兰

(北京教育学院数学系 100120)

伴随着某学校选修2-3排列组合教学的结束，2018年高考数学的第一轮复习悄然而至.由于排列组合内容相对独立，又刚刚学完，于是该校数学组打破已有的复习顺序，选择以此内容作为高考数学第一轮复习的起点.笔者受邀就排列组合复习与该校教师同课异构，并围绕高考第一轮复习的有关问题研讨.

1 学习内容的再认识

高考第一轮复习，对知识点的梳理是绕不过的话题，问题是梳理什么，怎样梳理是值得深思的.

现在不少教师都会在课前或课始布置学生自主完成知识梳理，有些教师要求学生使用思维导图或框图呈现结果，待课上交流后教师再适度指点.就形式而言，上述过程既体现了学生主体又显示了教师主导.但据笔者的课堂观察及浏览教师的教学设计，就内容而言，无论是学生的整理还是教师的指点，多数仅是简单重复逻辑结构，对所学内容再认识的高度不够.

再认识学习内容，除了对所学知识是什么的归纳概括，还要从不同的角度得出自己对所学内容的理解，以及应用策略的概括.

查缺补漏，提高能力是复习课的主要功能，因此什么是加法原理、乘法原理；什么是排列、组合；排列与组合的差别；排列与组合的公式等等，这些排列组合应知应会内容的整理记忆是需要的，但知识梳理的重点应是鉴别“缺”和“漏”.重点有四：(1)学生分别提供一个典型的排列、组合的例子，意图是考察学生是否基本理解了排列、组合的含义；(2)学生将已做过的有限制条件的排列或组合的习题归类，意图是考察学生是否真正理解了排列、组合的本质，以及概括的水平；(3)学生对(2)中的类型，尝试总结解决问题的思想方法或具体策略，意图是考察学生是否对各类问题有了正确的思路和具体的方法，还有哪些问题及解决问题的方法需要补充；(4)学生对排列或组合已有的错题分析，找到规避错误的方法，意图是帮助学生将错误转化为教育资源.当然上述四点，可根据复习课课时的总安排，分别进行.

知识点的梳理是复习的起点，也是再认识的过程，不仅要唤起学生已有的经验，还要从新的视角再认识.比如，已知排列或组合区别(是否有序)，还要再琢磨它们的联系.事实上排列问题都可分成两步完成：先组合，再全排列；同样，组合问题如若增加排序，亦可转为排列问题.同时要在新的情境再认识排列、组合，并结合具体的情境，让学生体会“一般”与“具体”的关系.

2 典型例题的逻辑性和拓展性

在高考基本稳定的前提下，以历年高考题或N模题为依据，然后归类复习无可厚非.但典型例题的选取切忌堆砌高考题或N模题，应引领学生研究这些题目，找到相关原题之间的逻辑性，并适度改编拓展.

本节复习课，笔者以“某高二年级期末考试的科目有8科”为背景，求解4次变式条件下安排考试方法的种数：⑴语数外三科考试不得相邻；⑵语数外三科考试必须排在一起；⑶语文考试必须在数学之前考；⑷数学不在第一和最后考.4个变式主要关注到的策略有不邻问题插空法；相邻问题捆绑法；特殊值法；否定肯定对等法；特殊元素/位置优先法.

最后变式问题：⑸某城市A、B两地之间有整齐的道路网(见图1), 从A到B最近距离的走法共有多少种？从A到B，横向走且仅走5段, 纵向走且仅走3段.于是问题⑸等价于5个“横”, 3个“纵” 排成一列的问题.由于是相同元素的排列，又等价：从8个位置任取5个排“横”, 剩余3个位置排“纵” 的问题.

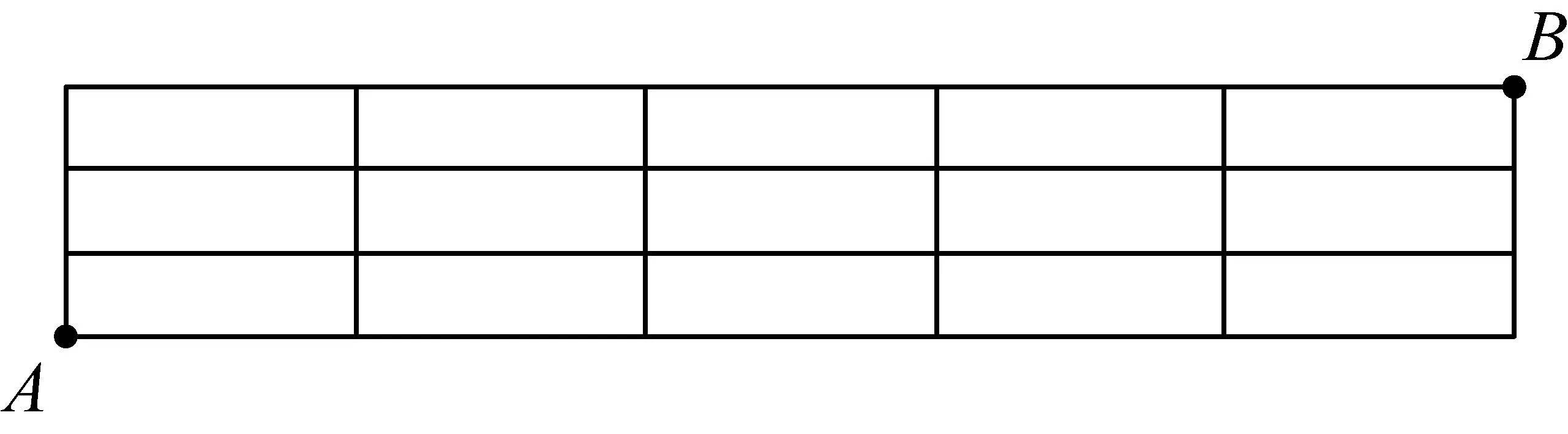
图1

5个变式，都可转化为8个元素有限制条件的排列或组合问题，这样一以贯之好处有四：一是省去理解不同背景的时间，但又强化了审题的重要性，因为条件细微的变化会导致截然不同的解题方法；二是将过去零散学习的类型和方法串起来，易发现各变式的联系与区别.特别是变式5将看似风马牛不相及的两个背景，找到相通之处，及异样之处(排列、组合)，领悟变与不变的美妙；三是复习一开始就将排列、组合问题综合考察(有教师先分开排列、组合，再综合复习)，虽然增加了挑战性，但没有跳出学生的最近发展区，而且也增强了学生分析解决排列、组合问题的能力；四是学生参与到题目的变式过程(课上先观摩教师是如何将题目变式的，教师要有意识地点拨，课下作业为模仿编改题)，达到知其然，知其所以然，知其将然.

3 思维参与和动机激发

排列、组合与其他知识关联较少，解决问题的具体计算也简单，但思维培养的机会很多.如，知识梳理；限制条件的分析、变式、转换；数学模型的抽象；解决方案正确合理的选择；多种解决方案的比较分析；归纳总结等.在复习中重视学生思维参与，不仅可以激发学生内在的学习积极性、创造性，提升思维能力，同时也能提升学生的学习能力.

美国心理学教授科勒(J.M.Keller)提出了ARCS模型，其中ARCS分别是影响学生学习动机的4要素的首字母：Attention(注意)、Relevance(相关)、Confidence(信心)、Satisfaction(满足)[1].该模式强调针对学生的动机水平和教学内容的特点，在教学过程中引起并维持学生的注意、构建教学与学生之间的关联、引发学生产生并支持完成学习的自信、最终体验到满足.

笔者创设的问题情境，就是以ARCS模型为指导，注重学生思维参与的活动.

上课伊始，笔者以到该校出行的真实场景为载体，创设问题情境：第一段出行(家→北京南苑机场)可供选择的交通工具有6种：自行车、私家车、出租车、公共汽车、机场大巴、地铁；第二段出行(北京南苑机场→某地机场)有两种方式，问有多少种出行方式？学生全部落入“陷阱”，齐答有12种，笔者反问第一段的条件充分吗？学生才意识到问题，于是笔者补充如下7个条件：(1)由于路途远，自行车不单独使用；(2)私家车仅从家出发；(3)没有直达的公共汽车；(4)家和机场大巴有一段距离；⑸家和机场都和地铁有一段距离；(6)最多利用三种不同交通工具，且三种之一是地铁；(7)不同种交通工具仅出现一次.

创设的情境，学生先是感觉非常容易，继而发现并不简单.在思维受阻后，笔者启发学生有序思考.先从大方向考虑，分两步(家→北京南苑机场；北京南苑机场→某地机场)解决问题；再考虑作为第一步(既是重点也是难点)如何解决，引导学生利用交通工具的数量(一种；两种；三种)或利用交通工具的种类(自行车；私家车；出租车；公共汽车；机场大巴；地铁)突破难点.

通过补充的7个条件，一方面让学生感受阅读大文本的策略，另一方面将分类相加，分步相乘，有序排列，无序组合(依据)；按照事件的结果分类，事件的发生过程分步(原则)；分类、分步不重不漏(底线)；特殊优先法、排除法、插空法(策略)等融入到问题解决中.高认知的系列问题，学法的指导，先独立思考再小组合作的教学策略，不仅引起并维持了学生的注意，激发了学生参与的信心，也撬动了学生思维的参与.

高考第一轮复习，提高学生参与的主动性和深度，将学生内在学习动机的激发和维持，思维的参与贯穿教学过程的始终，这该是数学有效复习所需要的.