基于最大似然算法的OFDM定时和频偏估计研究
王行建,张松
(中国电子科学研究院,北京 100041)
基于最大似然算法的OFDM定时和频偏估计研究
王行建,张松
(中国电子科学研究院,北京 100041)
OFDM系统对定时和载波频率偏差极其敏感,为了解决OFDM符号定时同步和载波频率同步的问题,采用基于循环前缀的最大似然估计算法,分析了对OFDM系统同步产生影响的三个主要因素,详细推导了基于循环前缀的最大似然估计算法,并针对最大似然估计算法在不同信道下的性能以及循环前缀长度对同步性能的影响进行了仿真分析,仿真结果对OFDM系统中循环前缀长度的选取具有指导意义。
OFDM 最大似然算法 循环前缀 定时估计 频偏估计
1 引言
OFDM(Orthogonal Frequency Division Multiplexing,正交频分复用)对定时误差和载波频率偏移等同步误差非常敏感,尤其是频偏将会导致系统性能的恶化[1]。目前,OFDM系统中有关定时和频率偏差估计的同步算法主要包括两大类:第一类是非盲算法[2-4],即基于训练符号的算法,这类算法会浪费带宽和功率资源,使通信系统的效率降低;另一类是盲算法[5-7],此算法基于OFDM符号中的CP(Cyclic Prefix,循环前缀),克服了训练符号浪费资源的缺点,提高了系统效率。
由于OFDM系统采用了插入循环前缀的方法来消除符号间串扰,文献[5]提出了一种利用循环前缀与OFDM符号中部分数据的相关性来完成联合符号定时粗估计和载波频率粗估计的最大似然估计算法。
本文分析了同步误差对OFDM系统的影响,并给出了相应的仿真结果,接着对最大似然估计器做了理论分析,得出影响算法性能的因素,然后针对循环前缀长度对同步性能的影响进行了仿真分析。
2 OFDM系统的同步
OFDM系统的同步包含载波同步、符号定时同步和样值同步三个方面[8]。如图1所示。
(1)载波同步。收发两端的振荡器频率不匹配,晶振或振荡器工作不稳定以及移动无线信道的多普勒效应,都会引起接收数据和本地载波之间的载波频率偏移。
(2)符号定时同步。由于接收机无法知道信道时延及接收数据符号的确切起始位置,因此需要符号定时同步来确定OFDM帧头位置和每个符号的起止时刻,以保证准确的CP去除和FFT窗口位置。将符号定时偏差关于采样周期归一化,由于小数倍的符号定时偏差能够通过信道均衡来消除,可以并作信道冲击响应的一部分,因此只考虑整数倍的符号定时偏差。
(3)样值同步。保证接收端确定每个符号的起止时刻和使接收端与发送端有相同的采样频率。
由于采样钟同步和一般数字通信系统的实现思想是一样的,本文仅论述符号定时同步和载波同步,而假设采样钟理想同步。
3 基于最大似然的定时和频偏估计
基于循环前缀的ML(Maximum Likelihood,最大似然)估计主要是利用OFDM符号中被复制的部分与循环前缀的相关性来估计符号定时和载波频偏[9]。
假设发送信号为s(k),每个符号包含N个子载波,循环前缀的长度为Ng,接收信号为:
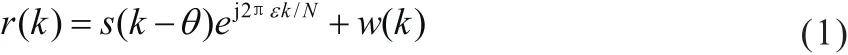
可以知道r(k)的连续2N+Ng个样值中一定包含一个完整的N+Ng符号。假设接收端认为OFDM符号的起始位置为θ。
定义I和I`两个集合如公式(2)所示:

其中集合I包含与集合I`中相同的元素,是第i个OFDM符号的循环前缀,接着定义向量r:

向量r包含2N+Ng个观察点,由于只有区间I和I`内的元素(即r(k),k∈I∪I`)具有对应相关性,所以有公式(4):
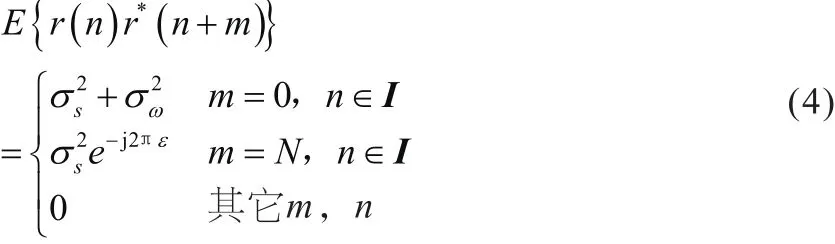
σs2和σω2分别为信号功率和噪声功率。概率密度函数f(r/θ,ε)的对数定义为对数似然函数Λ(θ,ε),即:

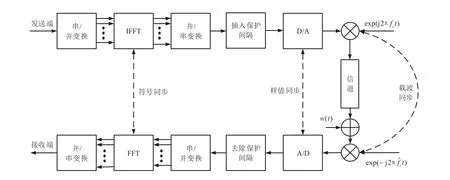
图1 OFDM系统的同步
其中f(r/θ,ε)表示给定符号到达时间θ和频率偏差ε条件下2N+Ng个抽样值的联合概率密度函数。因为对于一般的多载波系统,OFDM符号的子载波数量都比较大,由大数定理可得多载波系统的时域数据服从复高斯分布[10]。进而得到θ和ε的联合对数概率密度函数,如公式(6)所示:
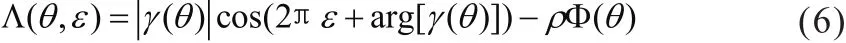
其中:
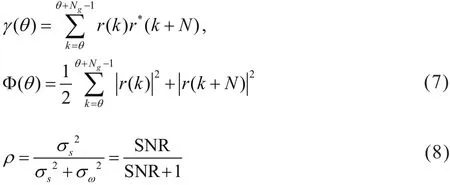
最大似然估计要求估计能够使得Λ(θ,ε)最大的θ和ε的取值,通常将(θ,ε)这个二维的问题求解分两步来完成:

要使得Λ(θ,ε)最大,首先要使公式(6)中的cos项等于1,即2πε+arg[γ(θ)]=2nπ,n为整数,可以推导出ε的最大似然估计般的,归一化载波偏移较小,因此取n=0,可以得到。令公式(6)中cos项为1,则θ的最大似 然函数为 Λ(θ, ε ˆML(θ) ) = γ( θ) - ρΦ (θ ),可以 看出上式是θ的函数,只和θ有关系。为了得到θ的估计值,最大化 Λ(θ, ε ˆML(θ)),然后将θ代入公式(6)就能够得到θ的估计,所以,θ和ε的联合最大似然估计就变为:
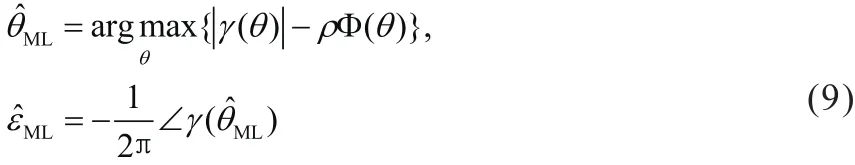
由以上推导可以得到如下结论,只有循环前缀的抽样数量Ng和信噪比SNR这两个参数影响着最大似然算法的性能,γ(θ)与Φ(θ)加权相加,会在 θˆML时刻出现峰值,同时 γ (θ ˆML)的相位与εˆML呈正比关系。
4 仿真结果与分析
仿真条件:N=256,SNR=25 dB,基带64QAM调制,所加定时偏移为200个样本值,归一化频偏为0.25,等幅两径信道的第二径比第一径延时30个采样点。图2至图8给出了在不同信道条件和不同CP长度下定时相关波形及频偏估计波形。由图可见,定时相关波形都在正确定时位置200处达到最大峰值,对应的相位即为频偏0.25,但相关峰值变化缓慢,不具有离散谱线的特点。比较图2、图3可以看出,当CP长度较短时,得到的相关峰明显变差;比较图4、图5、图6、图7,当为AWGN信道时,相关波形有明显的尖峰,而在等幅两径信道和瑞利多径信道时,出现了平顶现象,这就很容易引起定时位置的抖动。因为循环前缀与OFDM符号中被复制的部分的相关性,因此由图8可以看出,每个符号均得到了相关峰值。
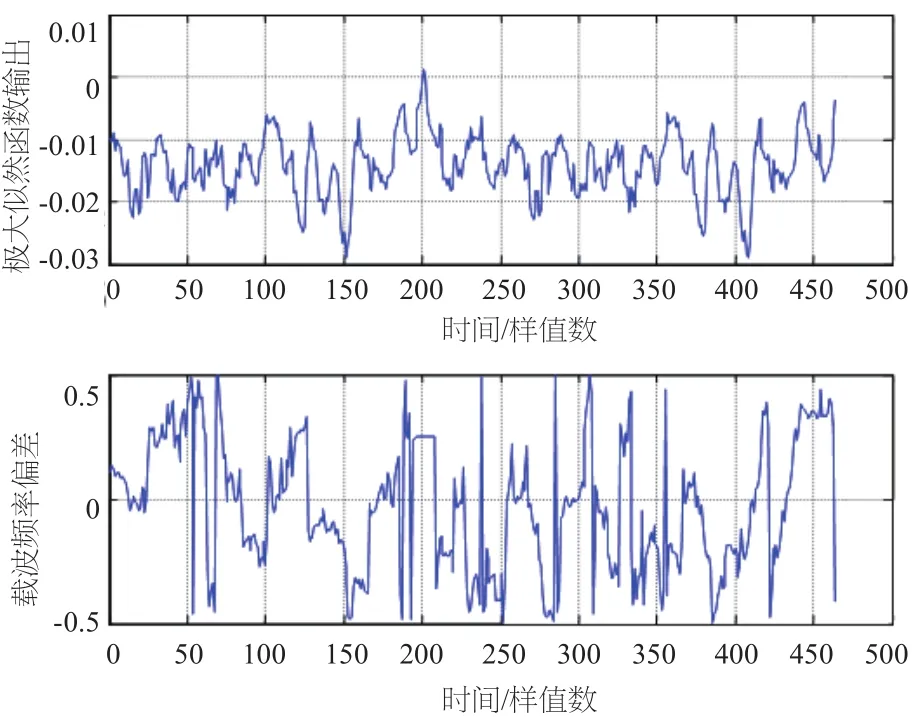
图2 定时相关波形及频偏估计波形(AWGN,CP=8)
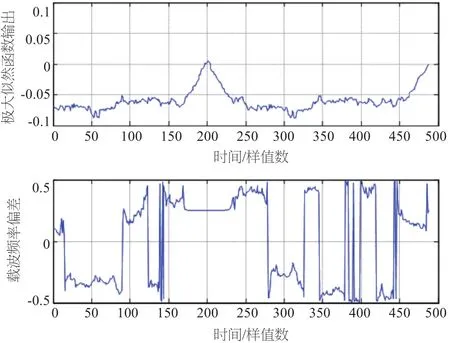
图3 定时相关波形及频偏估计波形(AWGN,CP=32)
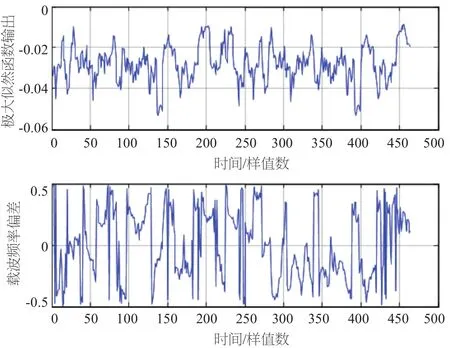
图4 定时相关波形及频偏估计波形(两径,CP=8)
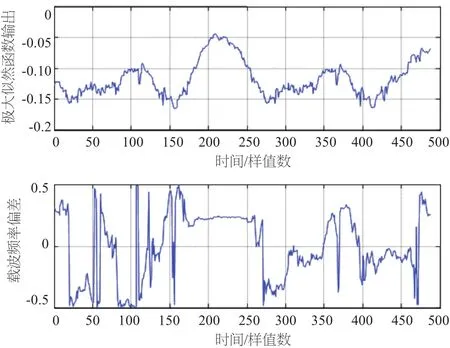
图5 定时相关波形及频偏估计波形(两径,CP=32)
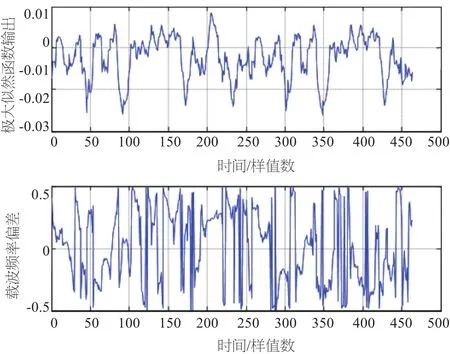
图6 定时相关波形及频偏估计波形(瑞利,CP=8)
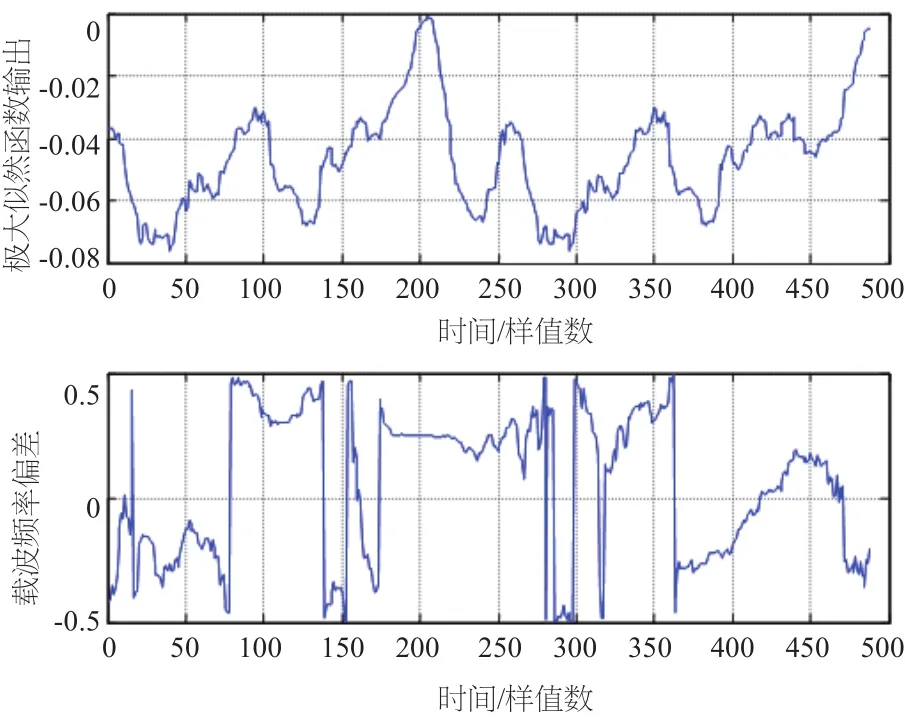
图7 定时相关波形及频偏估计波形(瑞利,CP=32)
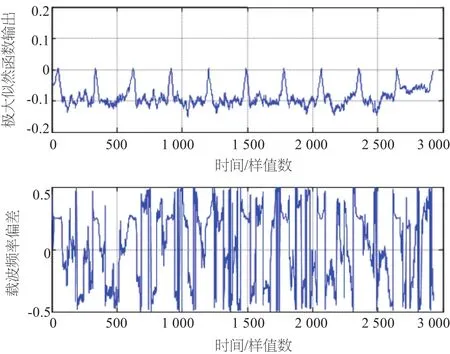
图8 定时相关波形及频偏估计波形(10个符号)
图9 、图10给出了在不同信道条件及不同CP长度下,定时和频偏估计的均方误差随信噪比变化的曲线图。N=256,基带64QAM调制,所加定时偏移为50个样本值,归一化频偏为0.25,等幅两径信道的第二径比第一径延时30个采样点。由图可以看出,在低信噪比条件下,增大循环前缀的长度可以明显地使符号定时和频偏估计的均方误差减小,而在信噪比较高时,增加循环前缀的长度对符号定时估计的影响不大,而频率偏差估计的性能略有改善。由于ML估计算法是针对AWGN信道设计的,在AWGN信道中,集合I和I`内的数据之间存在很好的相关性,而经过多径信道后,相关性被破坏了,从而致使频偏估计性能有所下降,而定时估计性能下降严重。但在实际中,由于通常采用高性能的信道估计和均衡技术,ML估计仍可以满足实际要求。
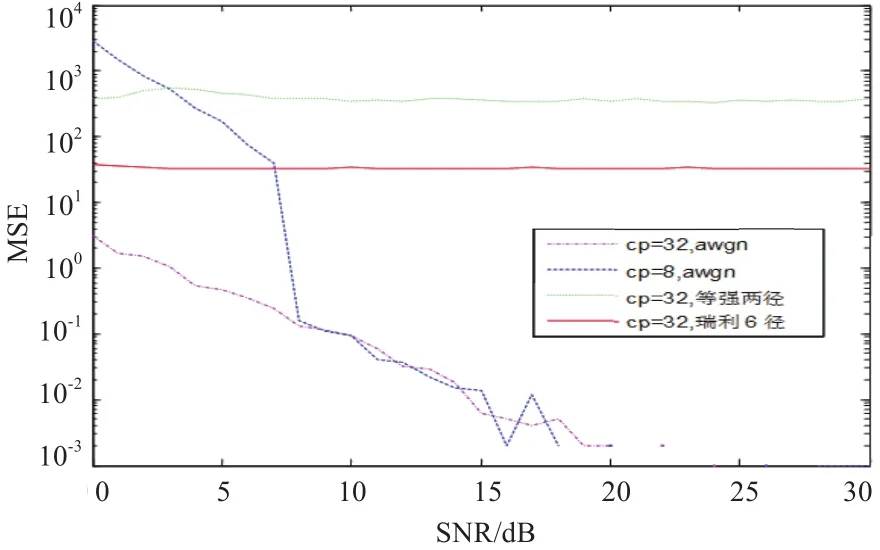
图9 ML定时估计均方误差图
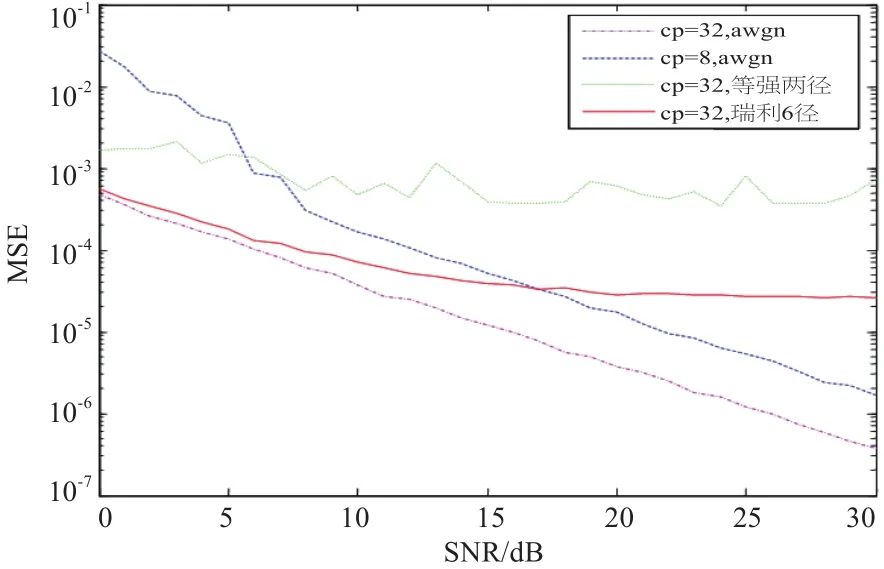
图10 ML频偏估计均方误差
5 结束语
本文分析了定时和频偏误差对OFDM系统的影响,并给出了仿真结果。理论分析了最大似然估计器,得出影响算法性能的因素,并针对循环前缀长度对同步性能的影响进行了仿真分析,仿真结果表明:AWGN信道在低信噪比时,增大循环前缀的长度可以明显地提高符号定时和频偏估计性能,而在信噪比较高时,增加循环前缀的长度对频率偏差估计的性能略有改善,而对符号定时估计的影响不明显。相比与AWGN信道多径信道下,ML算法性能恶化严重。
[1] 柴立凯. OFDM同步技术研究及实现[D]. 西安: 西安电子科技大学, 2014.
[2] SCHMIDL T M, COX D C. Robust frequency and timing synchronization for OFDM[J]. IEEE Transactions on Communications, 1997,45(12): 1613-1621.
[3] MINN H, ZENG M, BHARGAVA V K. On timing offset estimation for OFDM systems[J]. IEEE Communication Letters, 2000,4(7): 242-244.
[4] PARK B, CHEON H, KANG C, et al. A novel timing estimation method for OFDM systems[J]. IEEE Communication Letters, 2003,7(5): 239-241.
[5] VAN DE BEEK J J, SANDELL M, BORJESSON P O.ML estimation of time and frequency offset in OFDM systems[J]. IEEE Transactions on Signal Processing,1997,45(7): 1800-1805.
[6] TANDA M. Blind symbol-timing and frequency-offset estimation in OFDM systems with real data symbols[J].IEEE Transactions on Communications, 2004,52(10):1609-1612.
[7] CHIAVACCINI E, VITETTA G M. Maximum-likelihood frequency recovery for OFDM signals transmitted over multipath fading channels[J]. IEEE Transactions on Communications, 2004,52(2): 244-251.
[8] 王娜. 基于IEEE802.16e标准定时同步技术研究[D]. 西安: 西安电子科技大学, 2008.
[9] 方铁军. OFDM系统同步问题的研究[D]. 北京: 北京邮电大学, 2007.
[10] 南方. LTE下行链路高速铁路应用场景中的抗多普勒技术[D]. 西安: 西安电子科技大学, 2011. ★
Research on Timing and Frequency Offset Estimation Based on ML Algorithm for OFDM
WANG Xingjian, ZHANG Song
(China Academy of Electronic and Information Technology, Beijing 100041, China)
OFDM systems are extremely sensitive to timing offset and carrier frequency offset. In order to solve the problems of OFDM symbols timing synchronization and carrier frequency synchronization, the maximum likelihood estimation algorithm based on cyclic pre fi x was adopted. Three main factors affecting the synchronization of OFDM systems were analyzed and the maximum likelihood estimation algorithm based on cyclic pre fi x was deduced in detail. The performance of maximum likelihood estimation algorithm in different channels and the in fl uence of the length of cyclic pre fi x on the synchronization performance were simulated and analyzed. The simulation results have guiding signi fi cance for the selection of the length of cyclic pre fi x in OFDM systems.
OFDM maximum likelihood estimation algorithm cyclic pre fi x timing offset estimation frequency offset estimation
10.3969/j.issn.1006-1010.2017.21.009
TN911.23
A
1006-1010(2017)21-0042-05
王行建,张松. 基于最大似然算法的OFDM定时和频偏估计研究[J]. 移动通信, 2017,41(21): 42-46.
2017-11-08
黄耿东 huanggengdong@mbcom.cn

王行建:助理工程师,硕士毕业于西安电子科技大学,现任职于中国电子科学研究院,主要从事无线通信和数据链方面的研究工作。

张松:助理工程师,硕士毕业于北京交通大学,现任职于中国电子科学研究院,主要从事无线通信链路层方面的研究工作。

