如何做实证：相关性研究

喻 平

(南京师范大学课程与教学研究所 210097)

教育研究中，主要关心的是两个或多个变量之间是否存在某种关系.例如，个体的数学阅读成绩与逻辑思维能力之间是否存在内在联系？单凭经验，人们可以认为两者之间有联系，但是从研究的角度看，必须要用一定的方法和数据去验证它们之间的确存在内在联系.相关性研究，就是处理这类问题的一种方法.

相关性研究有两个目的：①探索变量之间的联系；②从被试在一个变量上的得分去预测他在另一个变量上的得分.在相关研究中，可以在相同的时间点或不同的时间点测量变量.在预测研究中，用于测量的变量必须在对被预测的变量进行测量之前作测量.[1]在数据分析方面，相关性研究的数据用相关系数和回归分析处理，预测性研究主要用回归分析处理.

1 相关性研究的设计

相关性研究的设计模式很简单、固定，整个过程如图1：

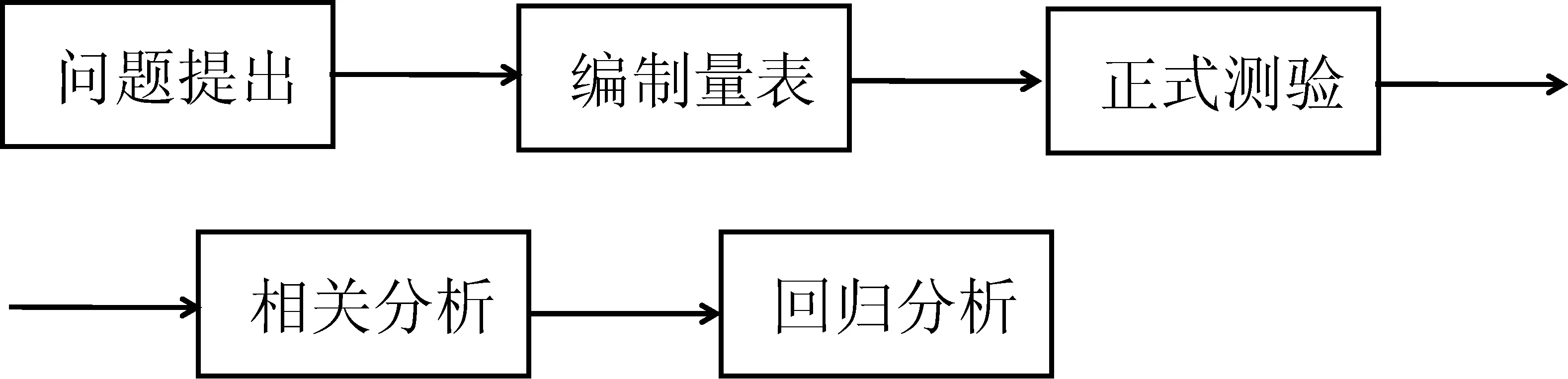
图1 相关性研究设计

1.1 问题提出

作为整个研究的起点，问题提出关系到研究是否有意义和价值，是否具有可操作性，因此，问题提出是研究的关键.

因为相关性研究是研究变量之间的关系，给人的错觉似乎可以把任意两个变量联系起来作为研究课题.例如，学生的逻辑思维发展可能与教师的教学方法有关系，但是与教师的生活习惯可能就没有什么关系，将后者作为研究问题可能是没有意义的.问题提出要基于几种途径：第一，对已有的研究进行全面考察，在别人研究的基础上得到启示，对别人的研究进行改造或拓展，从而提出新的问题.第二，在教学实践中发现和提出问题.例如，批改作业是数学教师一项必须做的工作，这项工作单调、枯燥、繁重，那么可以思考：批改作业的量对学生数学学业成绩有多大影响？作业批改方式对学生数学学业成绩有多大影响？选择这样的问题研究既有一定理论价值又对教学实践有直接的指导意义.第三，依据个人的经验提出问题.一线教师在长期的教学实践中积累了大量经验，这些经验是对自己教学实践的总结和提炼，于是可以判断某些因素之间可能存在的内在联系，在经验基础上提出的问题可以视为有一定依据.

诸如下面一些问题可以考虑用相关性研究的方法：(1)数学问题表征与解题成绩之间的关系；(2)个体认知结构对解题迁移的影响；(3)自我监控能力与数学思维品质的相关性；(4)逻辑推理能力与问题提出能力的关系；(5)6个数学核心素养(数学抽象、逻辑推理、数学建模、数学运算、直观想象、数据分析)之间的关系；(6)成就动机与数学学业成绩的关系；(7)学习焦虑与数学学业成绩的关系；(8)自我效能与数学学业成绩之间的关系；(9)学生课堂参与对数学交流的影响；(10)教师提问方式与学生课堂参与的关系；(11)教师的知识结构对教学设计的影响；(12)教师的认识信念对教学行为的影响；(13)教师的学科教学知识(PCK)与学生能力发展的关系.等等.当然，还可以考虑研究多个因素之间的关系，这些问题在教学实践中是非常多的.

1.2 编制量表

相关性研究最困难的地方就是编制量表，你要研究学生的直观想象能力，编制的量表却是考察学生的知识理解水平，两者差异太远，研究就会毫无效度可言.因此，量表编制必须按照严格的程序进行(见《如何做实证：测量研究》).如果研究两个变量之间的关系，就需要编制测量这两个变量的两份量表；如果研究多个变量之间的关系，就需要编制多份量表，每份量表测量一个变量.

1.3 正式测验

正式测验是指选择一组被试进行两次或多次测试.研究两个变量间的关系，一组被试需要做两份量表测试；研究多个变量之间的关系，一组被试需要做多份量表测试.如果只做相关性研究，那么两次或多次测验的时间可以不相同；如果要做预测性研究，那么两次测试之间要间隔较长时间.

下面对图1的后两个阶段作专门论述.

2 相关分析

2.1 相关关系的理解

我们知道，函数是讨论两个或多个变量之间的关系，一旦自变量给定一个值，因变量就有唯一的值对应，这是一种确定关系.相关关系不同，它是指两个变量之间不精确、不稳定的变化关系.例如，数学成绩和语文成绩有没有关系？有的学生数学、语文成绩都好，有的学生数学成绩好，语文成绩不好，有的学生正好相反.也就是说，数学成绩与语文成绩之间没有准确的计算公式可以表达，两个变量具有随机性，因此数学成绩和语文成绩之间就是一种相关关系.

相关关系分为正相关、负相关和零相关.正相关指两个变量的变化方向相同；负相关指两个变量的变化方向相反；零相关指两个变量之间没有相关.

相关关系不等于因果关系.A和B之间的相关，只能说明A与B有内在联系，可以意味着A是B的决定条件，也可以意味着B是A的决定条件，还可以意味着第三个变量X既决定A又决定B，或者A与B之间的关系是由人为因素造成的.换句话说，A与B之间存在相关关系并不意味着两者之间就是因果关系.

2.2 相关系数的计算

相关系数是一种特征量，用来描述两个变量相互之间的密切程度.相关系数r的值在区间[-1，1]内，其值越靠近-1或1，表明相关性越高.相关系数的计算有若干种方法，下面介绍两种常用的方法.

积差相关系数.这种方法是Pearson提出来的，其适用条件为：①两个变量都是连续型随机变量；②两个变量的总体都呈正态分布或接近正态分布；③两个变量的取值是一一对应数据；④两个变量之间呈线性关系.

等级相关系数.这种方法是Spearman提出来的，用来求两个顺序变量之间的相关系数，要求两个变量都至少是顺序变量(也可以是等距量表或比率量表)，但不一定要求它们服从正态分布.

相关系数的计算必须要作显著性检验，因为是取的小样本数据，样本数据计算出来的相关系数能否推广到总体，即如果总体数据作相关性计算，结果是否还是一样的.此时只能用样本数据估计总体数据，估计就有犯错误的风险，于是用犯错误的概率来描述，这个过程就是显著性检验.

2.3 用SPSS软件计算相关系数

案例1抽测17名学生，他们的逻辑思维能力成绩为X，数学学业成绩为Y，得到两组数据.请研究X与Y之间的相关性.

表1 10名学生的原始分数

这个问题测验用的两个量表都是以百分制记分的，属于连续随机变量，因此要采用积差相关系数的计算方法.

打开SPSS页面

(1)点击[变量视图]，定义两个变量X，Y.

(2)点击[数据视图]，输入数据.

(3)依次点击[分析]、[相关]、[双变量]，得到<二元变量相关分析>主对话框.

(4)将对话框左边变量X，Y调入右边下的<变量>矩形框内.

(5)选择Pearson，点击[确定].

对于多个变量的相关分析同样操作.

结果如表2：

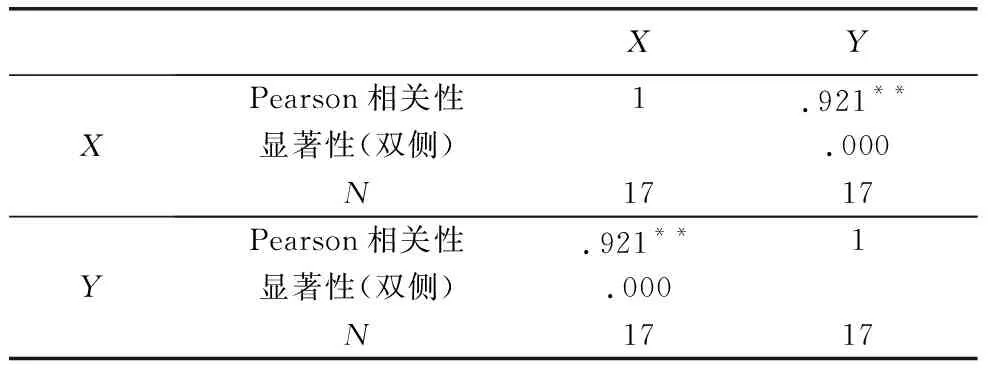
表2 逻辑思维能力与数学成绩的相关性

**.在 .01 水平(双侧)上显著相关.

表2表明，逻辑思维能力与数学学习成绩之间的相关系数为0.921，相关系数大，且在0.01水平上呈显著相关.

该研究中，需要编制一份逻辑思维能力测试量表，数学学业成绩可以用被试多次数学考试的平均成绩作为数据.表2的下半部分是重复数据，在论文写作中可以省略下半部分.

案例2教师对学生课堂参与程度采用10个等级的评价方式，如果两名教师对10名学生的评分等级如表3，试分析两名教师评分的相关程度.

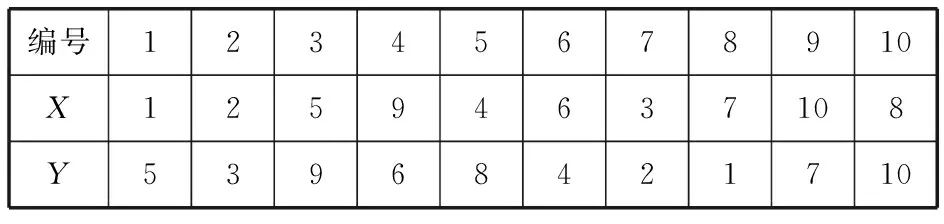
表3 两名教师对10名学生的评分等级

这个问题是等级评定方式，因此应当采用等级相关系数的计算方法.首先，将X的样本X1，X2，…，Xn按由小到大排列为1，2，…，n.将Y的样本Y1，Y2， …，Yn作相应的调整.得到

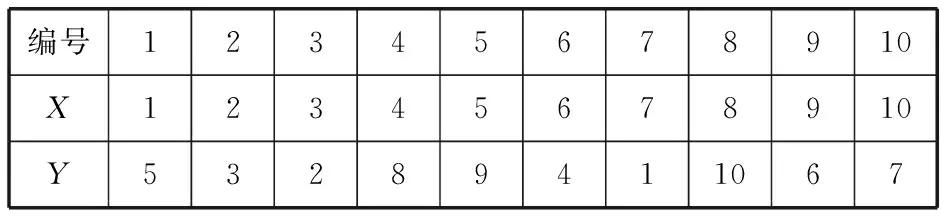
表4 排序后的数据分布

这个问题的计算与前面积差相关的计算方法步骤一样，只需在上面的计算程序第(5)步选择改为“Spearman或Kendall’s tau-b”即可.输出结果为：

表5 两个教师评价的相关系数

表5的结果表明，两个教师对学生的评价相关性很低(r=0.321)且没有显著性相关(0.365>0.05).

3 回归分析

3.1 回归方程概念

研究两个或多个变量之间联系的紧密程度可以采用相关分析方法，如果要根据一个或一组变量来估计或预测另一个变量的值，就需要建立变量间的回归方程，用回归分析的方法来完成.一般说来，如果用相关分析的方法发现两个变量之间相关性较高，那么可以考虑对其进行回归分析，这可以在一定程度上说明两者的依存关系.

在回归模型中，凡是变量之间存在线性关系的都称为线性回归模型，否则称为非线性回归模型.随机变量X和Y的样本点，在坐标系中是一个散点图，如果这些散点分布在一条直线周围，散点到该直线的距离之和最小，那么该直线就是这些点的线性回归方程.线性方程可以用最小二乘法求得.求出的线性方程必须检验，包括其一，检验自变量与因变量之间的关系能否用线性模型来表示；其二，检验各自变量对因变量的影响是否显著.求线性回归方程、检验过程都可以用SPSS软件完成.

3.2 线性回归方程的SPSS计算方法

1.一元线性回归的计算

案例3以案例1为例，探讨逻辑思维能力对数学学业成绩的预测作用.

(1)点击[变量视图]，定义变量X，Y.

(2)点击[数据视图]，输入数据.

(3)依次单击[分析]、[回归]、[线性]，弹出对话框.将左边源变量Y送入 <因变量>小框中，将X送入<自变量>小框中.

(4)点击[确定]，输出结果.

表6 模型汇总

a.预测变量: (常量),X.

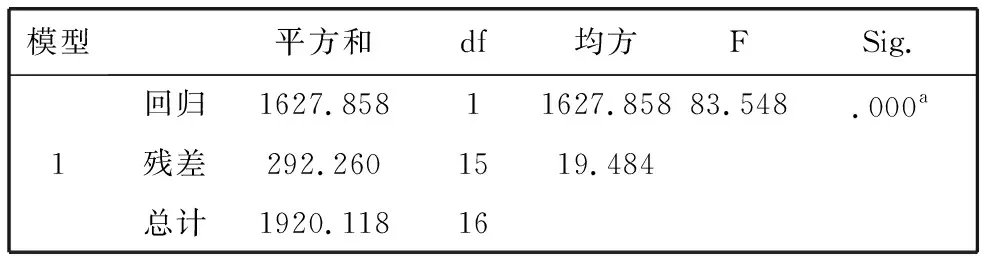
表7 方差分析b

a.预测变量: (常量),X.b.因变量:Y

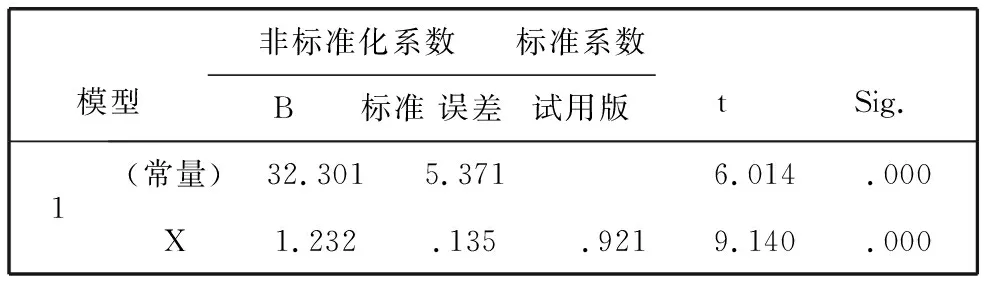
表8 系数a

a.因变量: Y

(1)在模型汇总表中，R是自变量与因变量的相关系数，R方是因变量的变异中被回归方程解释的比例，即数学成绩Y有84%是由逻辑思维X引起的.

(2)方差分析表检验回归模型，p=0.000，表示回归显著，即回归方程有较好的代表性.

(3)回归系数及检验表反映了回归系数和各系数的显著性检验，p=0.000，p=0.000，表明自变量对因变量的影响显著.

回归模型方程为Y=32.301+1.232X.

2.多元回归的计算

案例4假设因变量Y受到四个因素(X1，X2，X3，X4)的影响，数据见表9，建立回归方程.

表9 案例4的数据

(1)点击[变量视图]，将因变量定义为Y.将四个自变量依次定义为X1、X2、X3、X4.

(2)点击[数据视图]，输入数据.

(3)依次单击[分析]、[回归]、[线性]，弹出对话框.将左边源变量Y送入 <因变量>小框中，将X1、X2、X3、X4送入<自变量>小框中.

(4)单击[确定].

计算的结果见表10：

表10 方差分析

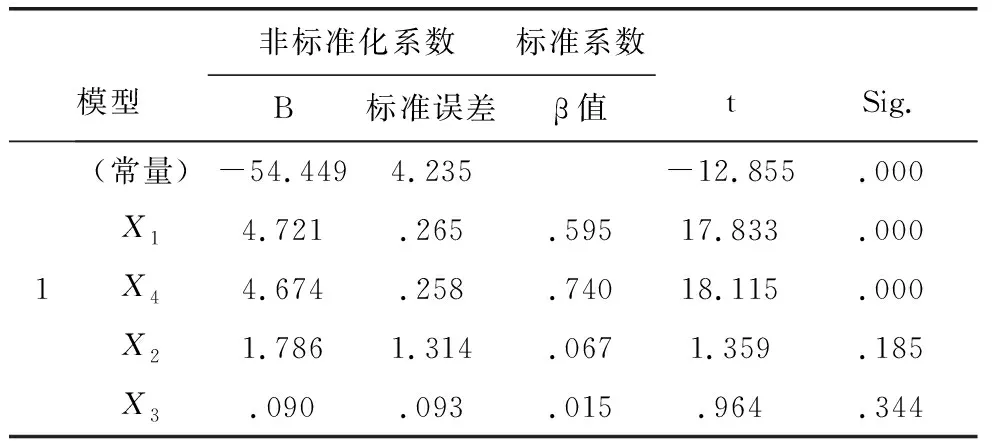
表11 系数a

由表11，得到回归方程：Y=-54.449-4.721X1-1.786X2+0.090X3+4.674X4.

表10显示，虽然回归模型显著(p=0.000<0.01)，但是系数b2，b3相应的显著性概率分别为0.185，0.344，它们均大于0.05，这两个变量在模型中不是重要变量，因此要删除X2和X3再进行回归.操作步骤就是在上面的计算程序第(3)步中，只将X1、X4送入<自变量>小框中.然后计算，结果见12，表13.

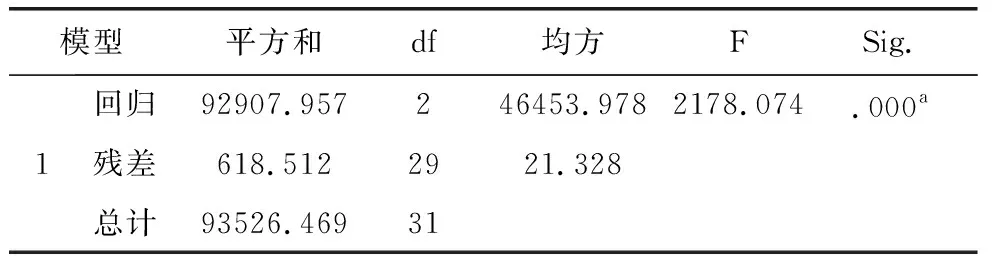
表12 删除X2和X3之后的方差分析

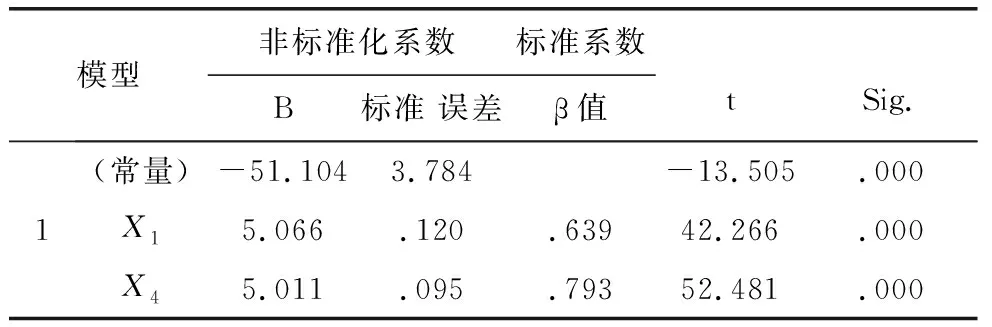
表13 删除X2和X3之后的系数a

因此，最后得到的回归方程为：Y=-51.104+5.066X1+5.011X4.

对于多元回归，有时计算出来的结果，会出现自变量的系数相应的显著性概率均大于0.05，此时可以考虑使用逐步回归的方法.逐步回归的基本思想是：首先将作用最显著的变量引入模型，在此基础上引进对模型作用最显著的第二个变量，引进变量后立即对原来引进的变量进行显著性检验，剔除不显著的变量，然后再引进新变量，直至既不能再引进变量又不能从模型中剔除变量为止.

案例5假定有一组变量，其中X1，X2，X3，X4是自变量，Y是因变量，自变量对因变量有影响，测得的数据如表14.试求Y对X1，X2，X3，X4的最佳线性模型.

表14 案例5的数据

作SPSS计算过程前面四步同案例4，计算结果见表15，表16.

表15 方差分析

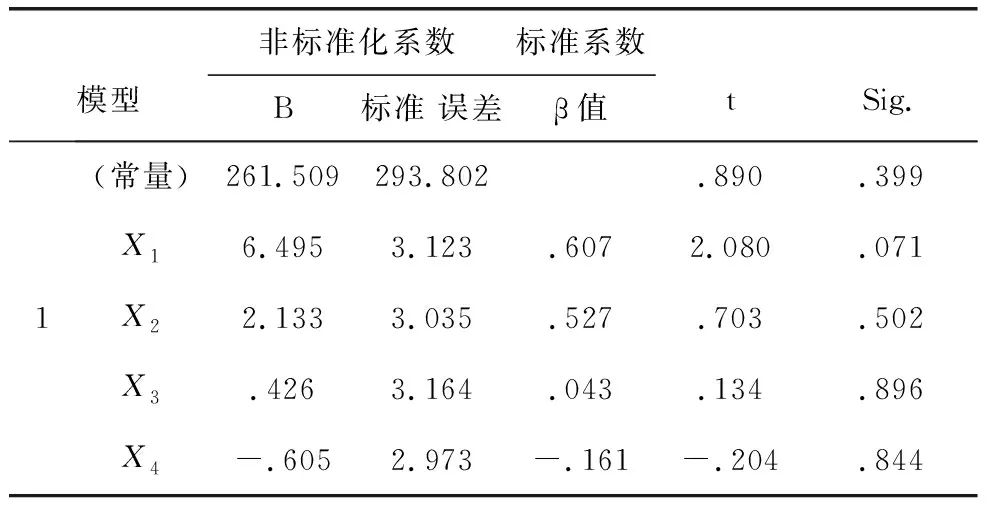
表16 系数a

由表16知，回归方程为：Y=261.509+6.495X1+2.133X2+0.426X3-0.605X4.

从表15知，p=0.000<0.01，回归模型非常显著.但是从表16中看到，系数b1，b2，b3，b4相应的显著性概率均大于0.05，所以没有一个变量在模型中是重要变量，因此需要对变量进行筛选，采用逐步回归法重新建立回归模型.方法是在前面四步的基础上，增加：

(5)选择<逐步回归>，点击[确定].

结果见表17，表18(输入/移出的变量表略，模型汇总表略，已排除的变量表略)：

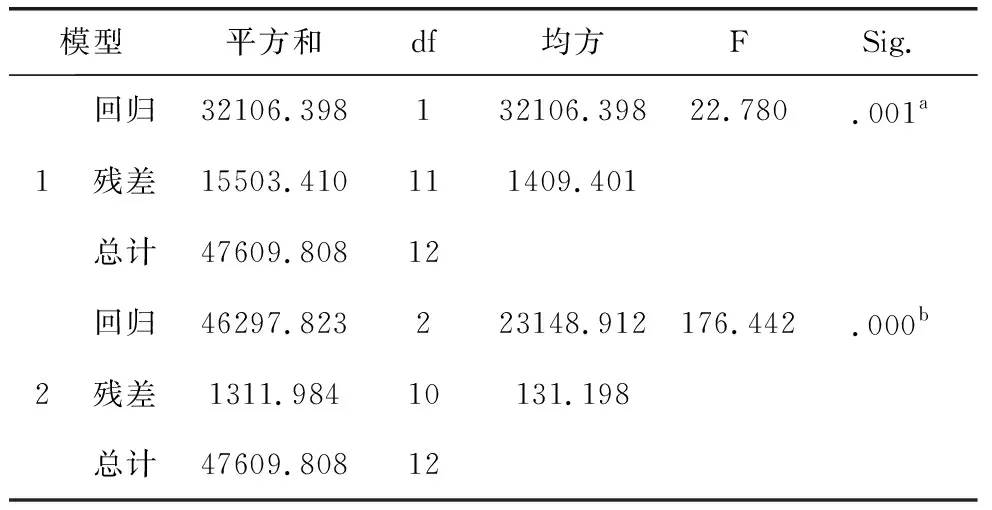
表17 逐步回归后的方差分析c

a.预测变量: (常量),X4.b.预测变量: (常量),X4,X1.c.因变量:Y

表18 逐步回归后的系数a

表17显示，第一个模型的p=0.001，第二个模型的p=0.000，它们的回归检验均具有非常高的显著性.由表18可知，第一次引进的变量X4得到的模型为：Y=492.239-3.09X4，第二次引进的变量X1得到的模型为：Y=431.636-2.57X4+6.031X1，这是最好的回归模型.